Алгоритм проведения занятий гр.1201-1204, 1231,1232, 1215, 1216, 1218, 1219
по разделу «Теорема об изменении кинетической энергии» 29.10.2020
Изучение разделов Лекций
Подключиться к bb.kai.ru
2. Зайти в курс «Теоретическая механика»
3. В меню слева зайти в «Обучающий материал»
4. Зайти в «Лекции»
5. Зайти в «Динамика материальной системы»
6. Зайти в подраздел «Тема 5.4 Теорема об изменении кинетической энергии»
Изучить тему:
Теорема об изменении кинетической энергии материальной системы.
2. Изучить материал:
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Введем понятие еще об одной основной динамической характеристике движения – о кинетической энергии.
Кинетической энергией материальной точки называется скалярная величина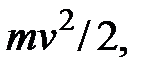 
равная половине произведения ее массы на квадрат ее скорости.
Единица измерения кинетической энергии та же, что и работы: в СИ – 1 Дж. Найдем зависимость, которой связаны эти две величины.
Рассмотрим материальную точку с массой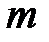 
, перемещающуюся из положения 
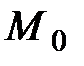, где она имела скорость 
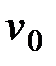, в положение 
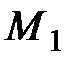, где ее скорость 
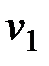. Для получения искомой зависимости обратимся к выражающему основной закон динамики уравнению 
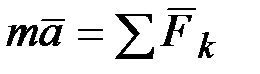. Проектируя обе его части на касательную 
к траектории точки 
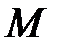, направленную в сторону движения, получим
.
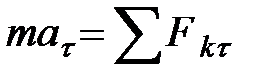Входящее сюда касательное ускорение точки представим в виде
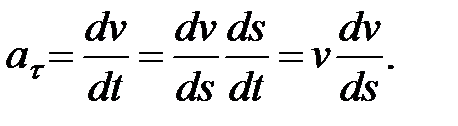
В результате найдем, что
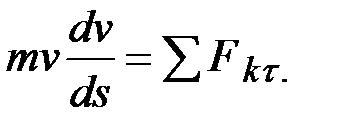
Умножим обе части этого равенства на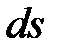 
и внесем 
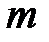под знак дифференциала. Тогда, замечая, что 
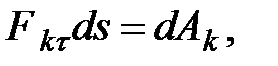где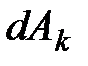 
- элементарная работа силы 
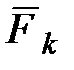, получим выражение теоремы о кинетической энергии для материальной точки в дифференциальной форме
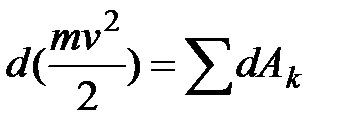. (38)
Теорема читается так:
полный дифференциал кинетической энергии материальной точки равен сумме элементарных работ всех действующих на нее сил.
|
|
Будем рассматривать все члены, входящие в равенство (38), как функции времени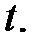 
Тогда, деля обе части его на 
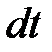и учитывая формулу (33), получим
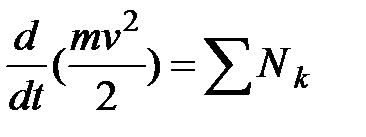, (39)
т.е. полная производная по времени от кинетической энергии материальной точки равна суммарной мощности всех действующих на нее сил.
Проинтегрировав теперь обе части равенства (38) в пределах, соответствующих значениям переменных в точках и , найдем окончательно
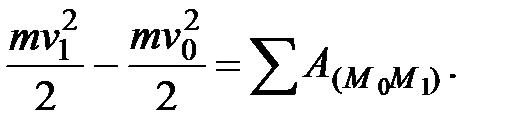(40)
Уравнение (40) выражает теорему об изменении кинетической энергии для материальной точки в конечном виде:
изменение кинетической энергии материальной точки при некотором ее перемещении равно сумме работ всех действующих на точку сил на том же перемещении.
С л у ч а й н е с в о б о д н о г о д в и ж е н и я. При несвободном движении точки в правую часть равенства (40) войдет работа заданных (активных) сил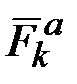 
и работа реакции связи. Ограничимся рассмотрением движения точки по неподвижной гладкой (лишенной трения) поверхности или кривой. В этом случае реакция 
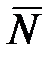(рис. 3.11) будет направлена по нормали к траектории точки и 
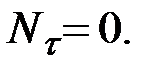Тогда, согласно формулы (31), работа реакции неподвижной гладкой поверхности (или кривой) при любом перемещении точки будет равна нулю, и из уравнения (40) получаем
.
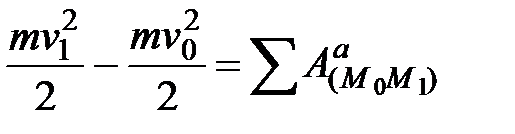Следовательно, при перемещении по неподвижной гладкой поверхности или кривой изменение кинетической энергии точки равно сумме работ на этом перемещении приложенных к точке активных сил.
Если поверхность (кривая) не является гладкой, то к работе активных сил прибавится работа силы трения. Если же поверхность (кривая) движется то абсолютное перемещение точки 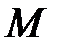может не быть перпендикулярно 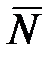и тогда работа реакции не будет равна нулю (например, работа реакции платформы лифта).
|
|
Р е ш е н и е з а д а ч. Теорема об изменении кинетической энергии (формула (40)) позволяет, зная как при движении точки изменяется ее скорость, определить работу действующих сил (первая задача динамики) или, зная работу действующих сил, определить, как изменяется при движении скорость точки (вторая задача динамики). При решении второй задачи, когда заданы силы, надо вычислить их работу. Как видно из приведенных выше формул для работ, это можно сделать, например, когда силы постоянны или зависят от положения точки. Таким образом, формулу (40) можно непосредственно использовать для решения второй задачи динамики, когда в задаче в число данных и искомых величин входят: действующие силы, перемещение точки и ее начальная и конечная скорости (т.е. величины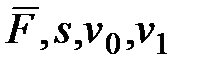 
), причем силы должны быть постоянными или зависящими только от положения (координат) точки.
Теорему в дифференциальной форме (формула (39)) можно, конечно, применять при любых действующих силах.
| M0 |
| M1 |
| M |
| H |
| r |
| R |
|
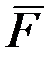
| Рис.3.13 |
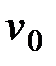надо сообщить телу, чтобы оно поднялось с поверхности Земли на заданную высоту 
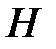(рис. 3.13). Силу притяжения считать изменяющейся обратно пропорционально квадрату расстояния до центра Земли. Сопротивлением воздуха пренебречь. Рассматривая тело как материальную точку с массой 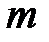, воспользуемся теоремой об изменении кинетической энергии|
|
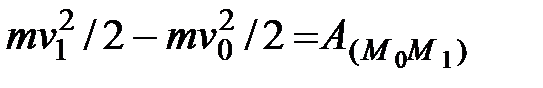(41)
Работу здесь совершает сила тяготения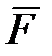 
. Тогда по формуле (37), учитывая, что в данном случае 
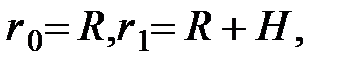где 
радиус Земли, получим
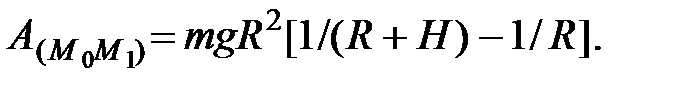
Так как в наивысшей точке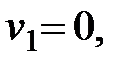 
то при найденном значении работы уравнение (41) дает
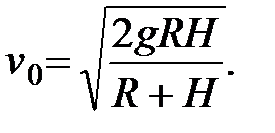
Рассмотрим частные случаи.
Пусть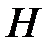 
очень мало по сравнению с 
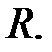Тогда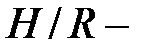 
величина, близкая к нулю. Деля числитель и знаменатель на 
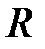, получим
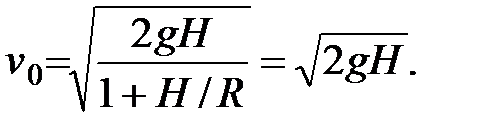
Таким образом, при малых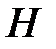 
приходим к известной формуле Галилея.
Найдем, при какой начальной скорости брошенное тело уйдет в бесконечность. Деля числитель и знаменатель на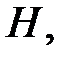 
получим
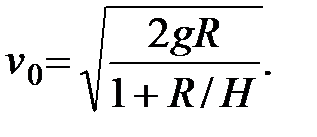
При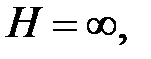 
считая средний радиус Земли 
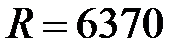км, находим
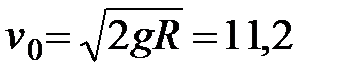км/с. (42)
Следовательно, тело, брошенное с поверхности Земли со скоростью 11,2км/с, навсегда покинет поле земного тяготения. Скорость, определяемая равенством (42), называется второй космической скоростью.
Можно доказать, что при начальных скоростях, лежащих приблизительно в пределах 8 км/c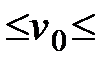 
11км/c, тело, брошенное по направлению касательной к земной поверхности, не упадет обратно на Землю, а превратится в искусственный спутник Земли. При начальных скоростях, меньших 8 км/c, или при негоризонтальном бросании тело, описав эллиптическую траекторию, упадет обратно на Землю. Такие траектории описывают ракеты дальнего действия, в частности, межконтинентальные. Все эти результаты относятся к движению в безвоздушном пространстве.
ПОНЯТИЕ О ПОТЕНЦИАЛЬНОМ СИЛОВОМ ПОЛЕ*
Часть (ограниченная или неограниченная) пространства, в каждой точке которого на находящуюся там материальную точку действует некоторая сила, зависящая только от положения точки, т.е. от ее координат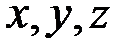 
называется силовым полем. Проекции 
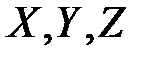силы поля на координатные оси являются некоторыми однозначными и непрерывными функциями от 
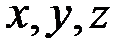,т.е.
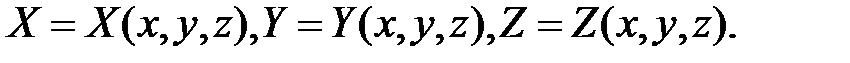
Допустим, что существует такая функция координат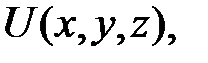 
частные производные которой по координатам равны проекциям силы поля на соответствующие координатные оси, т.е.
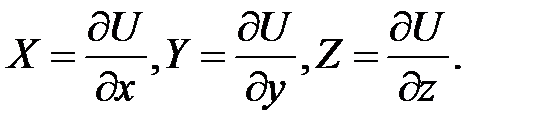(43)
Такая функция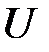 
называется силовой функцией данного силового поля, а силовое поле в этом случае называется потенциальным. Таково математическое определение силовой функции как функции, удовлетворяющей соотношениям (43). Выясним теперь ее физическое значение. Для этого найдем выражение элементарной работы силы потенциального поля. Эта работа равна
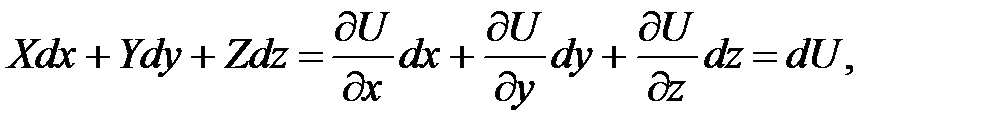(44)
т.е. элементарная работа силы потенциального поля равна полному дифференциалу силовой функции.
Следовательно, работа на конечном пути, когда точка приложения силы перемещается из положения в положение 
, выразится так
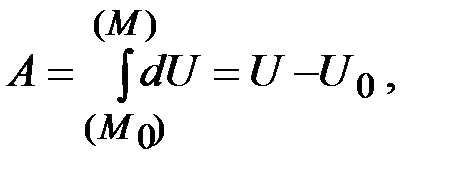(45)
т.е. работа силы потенциального поля равна разности значений силовой функции в конечной и начальной точках пути и, следовательно, не зависит ни от вида, ни от длины траектории, по которой перемещается точка приложения силы из положения 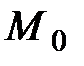в положение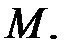 
Отсюда непосредственно следует, что в случае однозначной силовой функции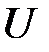 
работа силы потенциального поля на всякой замкнутой траектории равна нулю.
Независимость работы от вида пути и является основным свойством потенциального силового поля. Силы, действующие в нем, называются потенциальными. Силы, работа которых зависит от вида траектории или от закона движения точки приложения силы, называются непотенциальными. К таким силам относятся силы трения и сопротивления среды.
Если установлено, что соотношение (44) имеет место, то силовая функция находится из равенства
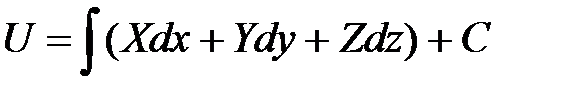. (46)
Постоянная 
здесь может иметь любое значение. Однако обычно условливаются в некоторой точке 
, называемой "нулевой точкой", величину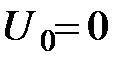 
и определяют исходя из этого условия.
Примерами потенциальных сил являются силы тяжести, упругости и тяготения в центральном поле. Покажем, что для полей этих сил действительно существуют силовые функции, и найдем их выражения. Поскольку под знаком интегралов, из которых получены формулы (34)-(36), стоят элементарные работы соответствующих сил, то придем к следующим результатам, используя равенство (46):
для поля с и л ы т я ж е с т и, если ось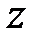 
направить вертикально вверх, 
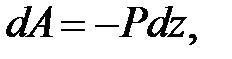откуда, считая 
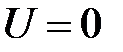при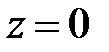 
(нулевая точка в начале координат), находим
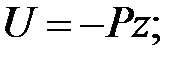(47)
для поля с и л ы у п р у г о с т и, действующей вдоль оси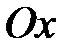 
(такое поле можно назвать линейным; в нем областью, в которой задано силовое поле, является прямая линия), 
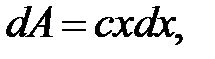откуда, считая 
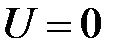при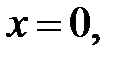 
находим
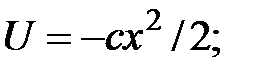(48)
для поля ц е н т р а л ь н о й с и л ы т я г о т е н и я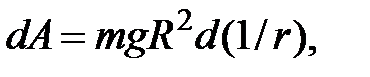 
откуда, считая 
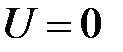при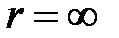 
(нулевая точка в бесконечности), находим
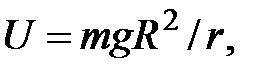(49)
где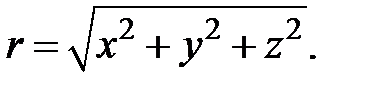 
Полагая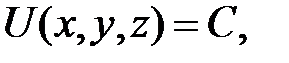 
где - некоторая постоянная, получим в пространстве уравнение поверхности, во всех точках которой функция 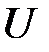имеет одно и то же значение. Такие поверхности называются поверхностями уровня или эквипотенциальными поверхностями. Если, как мы считаем, силовая функция является однозначной функцией координат, то поверхности уровня не могут пересекаться и через каждую точку поля проходит только одна поверхность уровня. При любом перемещении 
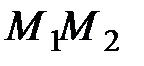вдоль поверхности уровня 
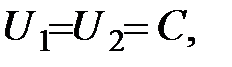и работа сил поля, как следует из уравнения (45), будет равна нулю. Поскольку сила при этом не равна нулю, то отсюда заключаем, что в любой точке потенциального силового поля сила направлена по нормали к поверхности уровня, проходящей через эту точку.
На рис. 3.14,а показаны две поверхности уровня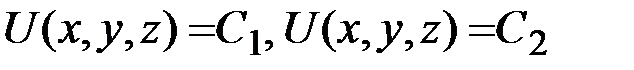 
, а на рис. 3.14,б – их сечение плоскостью, проходящей через нормаль 
.
| n |
| B |
| B1 |
|
| U=С1 |
| U=С2 |
| a) |
| б) |
|
|
|
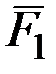
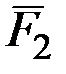
| B |
| B1 |
| D |
| D1 |
| U=C1 |
| U=C2 |
| Рис. 3.14 |
Если сила направлена в сторону, показанную на рисунке, то ее работа на перемещении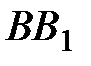 
будет положительна. Но по формуле (45) эта работа равна 
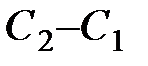. Следовательно, 
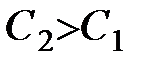, т.е. сила в потенциальном поле направлена в сторону возрастания силовой функции. Далее, работы силы 
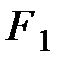на перемещении 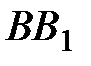и силы 
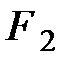на перемещении 
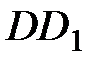одинаковы, так как равны 
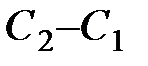. Но поскольку 
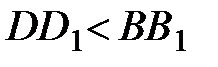, то должно быть 
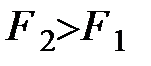. Следовательно, численно сила в потенциальном силовом поле больше там, где поверхности уровня проходят гуще. Отмеченные свойства позволяют наглядно представить картину распределения сил в потенциальном силовом поле с помощью поверхностей уровня. Кроме того, как видно из равенства (45), работа потенциальной силы зависит в конечном счете от того с какой поверхности уровня и на какую происходит перемещение точки.
Поясним сказанное примерами.
Для однородного поля сил тяжести (см. рис. 3.9), как видно из формулы (47),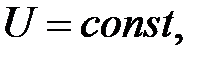 
когда 
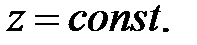Следовательно, поверхностями уровня являются горизонтальные плоскости. Сила тяжести 
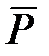направлена по нормали к этим плоскостям в сторону возрастания 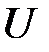и во всех точках поля постоянна.
Для центрального поля тяготения, согласно формулы (49),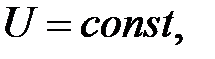 
когда 
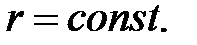Следовательно, поверхностями уровня являются концентрические сферы, центр которых совпадает с притягивающим центром. Сила в каждой точке поля направлена по нормали к соответствующей сфере в сторону возрастания 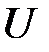(убывания 
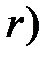, т.е. к центру сферы.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ*
Для потенциального силового поля можно ввести понятие о потенциальной энергии как о величине, характеризующей "запас работы", которым обладает материальная точка в данном центре силового поля. Чтобы сравнивать между собой эти "запасы работы", нужно условиться о выборе нулевой точки , в которой будем считать условно "запас работы" равным нулю (выбор нулевой точки, как всякого начала отсчета, производится произвольно).
Потенциальной энергией материальной точки в данном положении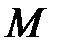 
называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое
П= А(МО).
Из определения следует, что потенциальная энергия П зависит от координат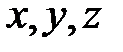 
точки М, т.е. что П=П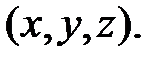 
Будем в дальнейшем считать нулевые точки для функций П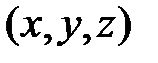 
и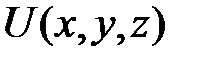 
совпадающими. Тогда 
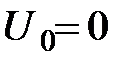и по формуле (45) 
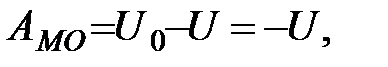где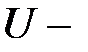 
значение силовой функции в точке М поля. Таким образом
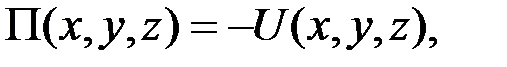
т.е. потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком.
Отсюда видно, что при рассмотрении всех свойств потенциального силового поля вместо силовой функции можно пользоваться понятием потенциальной энергии. В частности, работу потенциальной силы вместо равенства (45) можно вычислить по формуле
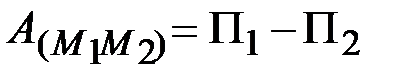, (50)
Следовательно,
работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном ее положениях.
Выражения потенциальной энергии для известных нам потенциальных силовых полей можно найти из равенств (47)-(49), учитывая, что П=-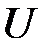 
. Таким образом, будет
для поля с и л ы т я ж е с т и (ось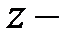 
вертикально вверх)
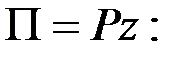(51)
для поля с и л ы у п р у г о с т и (линейного)
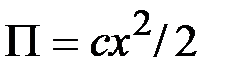; (52)
для поля ц е н т р а л ь н о й с и л ы т я г о т е н и я
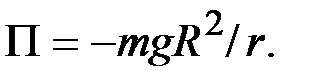(53)
Пусть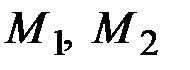 
будут два различных положения материальной точки, движущейся в потенциальном силовом поле, а 
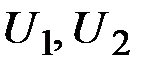- соответствующие значения силовой функции в этих точках. Напишем уравнение кинетической энергии
,
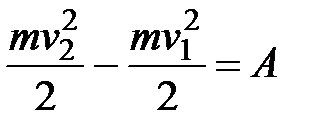где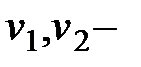 
скорости движущейся точки в положениях 
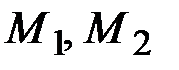. Но так как работа А равна разности значений силовой функции в конечном и начальном положениях движущейся точки, то
.
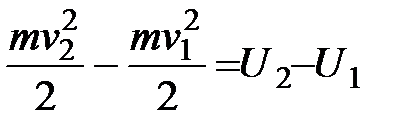Но потенциальная энергия в точках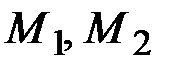 
будет выражаться так
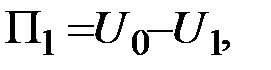
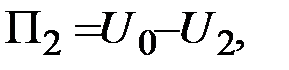
Следовательно
.
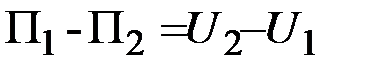Подставляя это выражение в уравнение кинетической энергии, получим
,
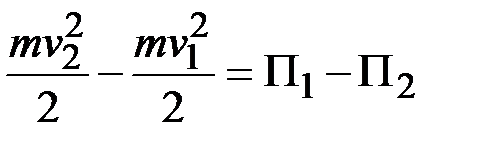или
= 
,
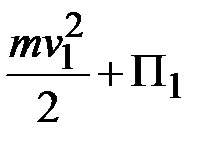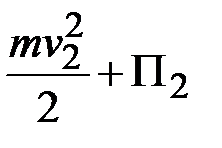т.е.
= 
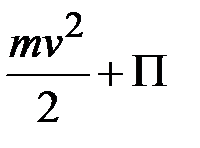(54)
Следовательно,
при движении материальной точки в потенциальном силовом поле сумма кинетической и потенциальной энергий ее остается постоянной.
Этот результат, выражающий сохранение полной механической энергии, представляет собой частный случай общего физического закона сохранения и превращения энергии
Контрольные вопросы.
1. Что называется силовым полем?
2. Что называется силовой функцией?
3. Что такое потенциальное силовое поле?
4. В чем состоит основное свойство потенциального силового поля?
5. Какие силы называются непотенциальными?
6. Какие поверхности называются эквипотенциальными?
7. Приведите примеры потенциальных силовых полей.
8. Что называется потенциальной энергией?
9. В чем заключается закон сохранения механической энергии?
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СИСТЕМЫ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ*
Потенциальная энергия системы определяется так же, как и для одной материальной точки, а именно:
потенциальная энергия П механической системы в данном ее положении равна работе, которую произведут силы поля при перемещении системы из данного положения в нулевое,
т.е.
П=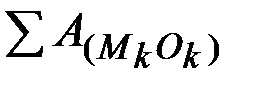 
.
При наличии нескольких полей (например, полей силы тяжести и сил упругости) для каждого поля можно брать свое нулевое положение.
Зависимость между потенциальной энергией и силовой функцией для системы будет такой же, как и для одной точки, т.е.
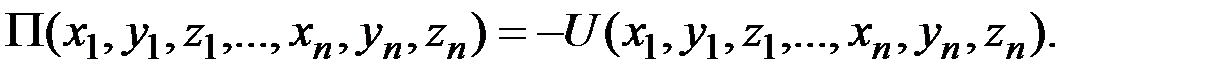
Допустим, что все действующие на систему внешние и внутренние силы потенциальны. В этом случае говорят, что система движется в потенциальном силовом поле. При перемещении в нем имеет место формула
.
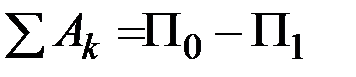Подставляя это выражение работы в теорему об изменении кинетической энергии системы в интегральной форме (100), получим для любого положения системы: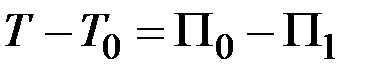 
или
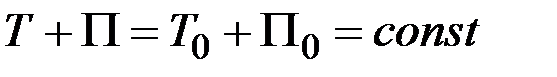(101)
Следовательно,
при движении под действием потенциальных сил (или при движении в потенциальном силовом поле) сумма кинетической и потенциальной энергий системы в каждом ее положении остается величиной постоянной. В этом состоит закон сохранения механической энергии,
являющийся частным случаем общего физического закона сохранения и превращения энергии. Величина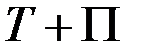 
называется полной механической энергией системы, а сама механическая система, для которой выполняется закон (101),- консервативной системой.
7. Зайти в «Практические занятия»
8. Зайти в «Динамика материальной системы»
9. Зайти в подраздел «Теорема об изменении кинетической энергии материальной системы»
10. Изучить материал подраздела «Теорема об изменении кинетической энергии системы»
Разобрать Примеры решения задач: Задача 38.44 (И.В.Мещерский),
Задача 38.27 (И.В. Мещерский).
* Раздел для самостоятельной работы студентов
* Раздел для самостоятельной работы студентов
* раздел для самостоятельной работы студентов