Пример 1. Смеситель с истечением по принципу сообщающихся сосудов
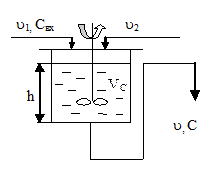
Математическая модель объекта
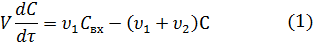
Начальное условие: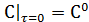 
Для условий статики:
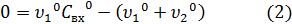
Истечение организовано по принципу сообщающих сосудов. В этом случае, объём жидкости в смесителе всегда величина постоянная V=const,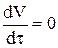 
, поэтому 
.
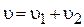Рассмотрим вариант линеаризации математической модели объекта по заданному каналу - u1→С.
Разложим входную и выходную переменные динамического канала в ряд Тейлора в окрестности стационарной точки, ограничившись линейными членами разложения:
; 
.
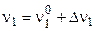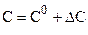Шаг 1. Подставим разложенные функции в уравнения модели:
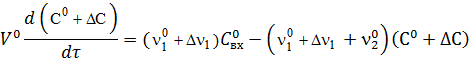
Шаг 2. Выполним алгебраические преобразования, сократим малые величины и вычтем соответствующее уравнение статики
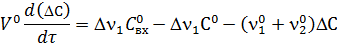
Шаг 3. Сгруппируем переменные:
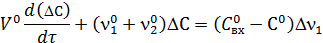
Шаг 4. Поделим левые правые части уравнения на (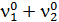
) при DС. Получим
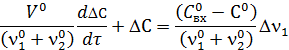
Обозначим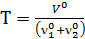 
; 
.
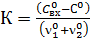Уравнение примет вид:
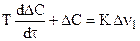(3)
Начальное условие: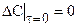 
.
Уравнение (3) представляет собой линеаризованное дифференциальное уравнение в отклонениях, связывающее входную и выходную переменные по каналу регулирования Dn1®DС.
Шаг 5. Преобразуем уравнение (3) по Лапласу:
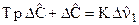или
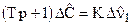, (4)
где р – комплексная переменная;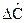 
, 
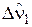- изображения переменных.
Определим передаточную функцию по каналу n1®С:
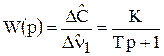. (5)
Полученная передаточная функция соответствует передаточной функции апериодического звена. Параметры звена: коэффициент К – это коэффициент усиления (или передачи); коэффициент Т – это постоянная времени, характеризующая инерционность объекта по данному каналу.
Пример 2. Теплообменник смешения со свободным истечением жидкости
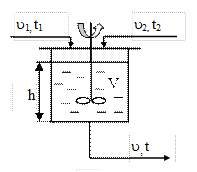
Уравнения модели для условий динамики:
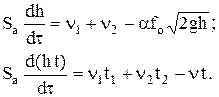(6)
Начальные условия: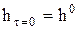 
, 
.
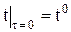Математическая модель для условий статики:
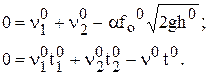(7)
Необходимо линеаризовать модель ХТП как объекта регулирования температуры. В качестве регулирующей переменной принять расход первого потока n1. Получить передаточную функцию по этому каналу (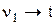
).
Расход первого потока n1 является входной переменной, изменение которой приведет к изменению температуры жидкости на выходе из теплообменника t и уровню жидкости в теплообменнике h. Таким образом, возникают динамические связи: 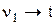и 
.
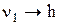Разложим входные и выходные переменные динамических каналов в ряд Тейлора в окрестности стационарной точки, ограничившись линейными членами разложения:
; 
; 
.
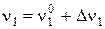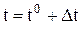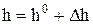Остальные переменные равны значениям в стационарной точке:
; 
; 
; 
.
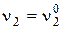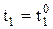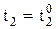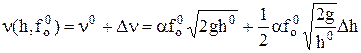Шаг 1. Подставим разложенные функции в уравнения модели:
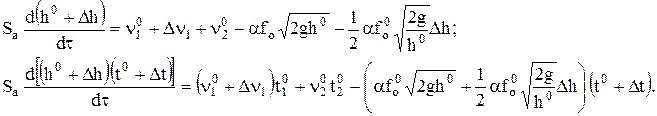
В соответствии с правилами дифференцирования производная от произведения переменных во втором уравнении разложится:
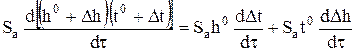. (8)
Выполним алгебраические преобразования, сократим малые величины и заменим второе слагаемое в уравнении (8) на уравнение материального баланса.
Уравнение теплового баланса запишется:
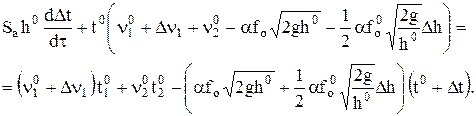
Раскрыв скобки и выполнив необходимые преобразования, получим:
.
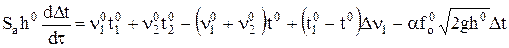Шаг 2. Вычтем соответствующее уравнение статики с учетом, что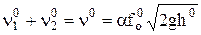 
:
.
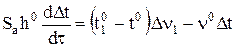Шаг 3. Сгруппируем переменные:
.
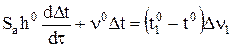Шаг 4. Поделим левые правые части уравнения на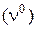 
при Dt. Получим
.
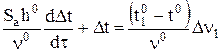Обозначим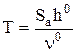 
; 
.
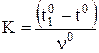Уравнение примет вид:
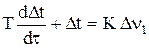. (9)
Начальное условие: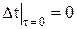 
.
Уравнение (9) представляет собой линеаризованное дифференциальное уравнение в отклонениях, связывающее входную и выходную переменные по каналу регулирования n1®t.
Шаг 5. Преобразуем уравнение (9) по Лапласу:
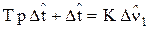или
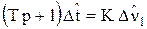, (10)
где р – комплексная переменная;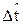 
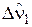, - изображения переменных.
Определим передаточную функцию по каналу n1®t:
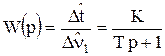. (11)
Полученная передаточная функция соответствует передаточной функции апериодического звена. Параметры звена: коэффициент К – это коэффициент усиления (или передачи); коэффициент Т – это постоянная времени, характеризующая инерционность объекта по данному каналу.