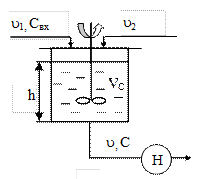
Уравнения математической модели для условий динамики:


Начальные условия: 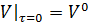 ;
; 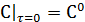 .
.
В соответствии с правилами дифференцирования производная от произведения переменных в уравнении (13) разложится:

Заменим второе слагаемое в уравнении (14) на уравнение материального баланса (12), тогда
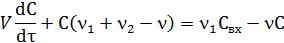
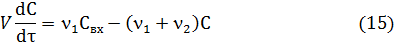
Таким образом, уравнения математической модели для условий динамики - это система уравнений (12, 15).
Соответствующие уравнения статики:
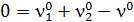 (16)
(16)
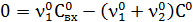 (17)
(17)
Необходимо линеаризовать модель ХТП как объекта регулирования концентрации. В качестве регулирующей переменной принять расход разбавителя n2 (n2→С).
Расход второго потока n2 является входной переменной, изменение которой приведет к изменению концентрации компонента на выходе из смесителя С и уровню жидкости в аппарате h (V). Таким образом, возникают динамические связи: 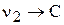 и
и 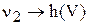 .
.
Так как мы предварительно в уравнении (13) разложили производную и фактически объединили уравнение (13) и (12) в одно уравнение (15), то для линеаризации можно использовать только одно уравнение материального баланса по компоненту (15).
Разложим входную и выходные переменные динамических каналов в ряд Тейлора в окрестности стационарной точки, ограничившись линейными членами разложения:
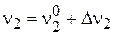 ;
; 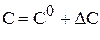 ;
; 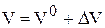 .
.
Шаг 1. Подставим разложенные функции в уравнения модели:
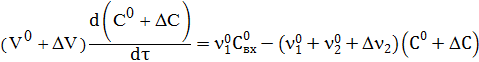
Шаг 2. Выполним алгебраические преобразования, сократим малые величины и вычтем соответствующее уравнение статики (17)
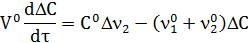
Шаг 3. Сгруппируем переменные:
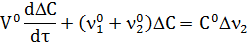
Шаг 4. Поделим левые правые части уравнения на (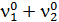 ) при DС. Получим
) при DС. Получим
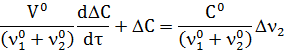
Обозначим 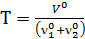 ; K
; K 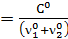 .
.
Уравнение примет вид:
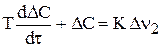 (18)
(18)
Начальное условие: 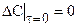 .
.
Уравнение (18) представляет собой линеаризованное дифференциальное уравнение в отклонениях, связывающее входную и выходную переменные по каналу регулирования Dn2®DС.
Шаг 5. Преобразуем уравнение (3) по Лапласу:
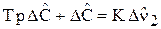 или
или
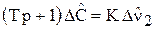 , (19)
, (19)
где р – комплексная переменная; 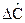 ,
, 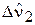 - изображения переменных.
- изображения переменных.
Определим передаточную функцию по каналу n2®С:
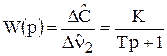 . (20)
. (20)
Пример 4. Рассмотрим предыдущий объект (см Пример 3).
Необходимо линеаризовать модель ХТП как объекта регулирования уровня (или объема). В качестве регулирующей переменной принять расход разбавителя n2 (канал n2→V).
Влияние расхода на объем отражено в общем материальном балансе (ур.12). Кроме этого, расход разбавителя влияет и на концентрацию, но концентрация не влияет на объем. Поэтому для получения передаточной функции по каналу n2→V достаточно линеаризовать только уравнение (12).
Разложим входную и выходную переменные динамического канала в ряд Тейлора в окрестности стационарной точки, ограничившись линейными членами разложения:
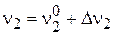 ;
; 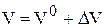 .
.
Шаг 1. Подставим разложенные функции в уравнения модели:
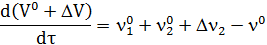
Шаг 2. Выполним алгебраические преобразования и вычтем соответствующее уравнение статики (16)

Уравнение (21) является линеаризованным дифференциальным уравнением в отклонениях, связывающее входную и выходную переменные по каналу регулирования Dn2®DV при соответствующем нулевом начальном условии 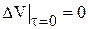 .
.
Преобразуем уравнение (21) по Лапласу
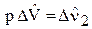 (22)
(22)
Передаточная функция по каналу n2®V:
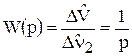 . (22)
. (22)
Полученная передаточная функция соответствует передаточной функции интегрирующего звена.