ЗАДАНИЕ 1.
ЗАДАНИЕ 2.
а) Выполнить действия над комплексными числами в алгебраической форме:
1)  16)
16) 
2) 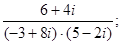 17)
17) 
3)  18)
18) 
4)  19)
19) 
5)  20)
20) 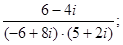
6) 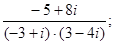 21)
21) 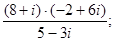
7)  22)
22) 
8)  23)
23) 
9)  24)
24) 
10)  25)
25) 
11)  26)
26) 
12)  27)
27) 
13)  28)
28) 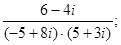
14)  29)
29) 
15)  30)
30) 
б) Выполнить действия над комплексными числами, используя тригонометрическую форму комплексного числа:
1)  16)
16)  ;
;
2)  ; 17)
; 17) 
3)  ; 18)
; 18)  ;
;
4) 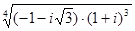 ; 19)
; 19)  ;
;
5)  20)
20) 
6)  ; 21)
; 21) 
7)  ; 22)
; 22) 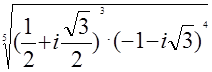 ;
;
8)  ; 23)
; 23) 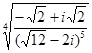
9)  ; 24)
; 24)  ;
;
10)  ; 25)
; 25) 
11)  ; 26)
; 26)  ;
;
12)  27)
27)  ;
;
13) 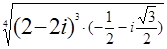 ; 28)
; 28)  ;
;
14) 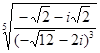 ; 29)
; 29) 
15)  ; 30)
; 30)  ;
;
ЗАДАНИЕ 1. Установить вид формулы логики высказываний:
 |  |
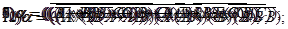 |
 |
ЗАДАНИЕ 4. Дан треугольник АВС. Найти:
а) уравнения сторон треугольника;
б) уравнение высоты, опущенной из вершины А на сторону ВС;
в) уравнение прямой, проходящей через вершину В параллельно стороне АС;
г) расстояние от вершины С до стороны АВ;
д) угол АВС.
Сделать чертеж:
1) А(3,-1), В(-1,7), С(2,5); 20) А(8,6), В(-10,5), С(-8,-7);
2) А(-2,5), В(7,-2), С(5,0); 21) А(-7,3), В(6,-5), С(3,5);
3) А(4,4), В(-10,2), С(2,-8); 22) А(4,-6), В(-10,4), С(9,8);
4) А(6,-4), В(4,10), С(-8,4); 23) А(1,2), В(2,-6), С(-5,4);
5) А(4,6), В(6,-9), С(-2,10); 24) А(1,-8), В(-5,2), С(4,10);
6) А(-6,5), В(9,-4), С(5,9); 25) А(-2,-5), В(7,2), С(-5,0);
7) А(-7,5), В(-9,-4), С(4,5); 26) А(-6,5), В(-4,9), С(6,11);
8) А(3,-5), В(8,7), С(-5,-10); 27) А(4,-9), В(7,4), С(-2,-6);
9) А(-10,4), В(7,-8), С(8,5); 28) А(-4,6), В(6,-9), С(2,10);
10) А(10,-6), В(-2,8), С(6,4); 29) А(4,-2), В(0,7), С(-1,5);
11) А(-8,-2), В(6,9), С(-7,3); 30) А(-4,-2), В(8,7), С(2,-5);
12) А(1,8), В(-5,2), С(4,-10);
13) А(-4,9), В(7,4), С(-2,6);
14) А(1,-2), В(2,-6), С(5,4);
15) А(6,5), В(-4,9), С(6,-11);
16) А(-9,3), В(4,-6), С(9,5);
17) А(5,-6), В(9,4), С(-11,4);
18) А(7,2), В(-5,7), С(3,-1);
19) А(-2,3), В(5,-3), С(7,7);
ЗАДАНИЕ 5. Решить комбинаторные задачи:
1. а) Сколькими способами читатель может выбрать две книги из 60 имеющихся?
б) В цветочном магазине продаются цветы 6 сортов. Сколькими способами можно составить букет из 7 цветов?
2. а) Сколькими способами можно разложить 8 различных писем по восьми конвертам, если в каждый конверт кладется только одно письмо?
б) Сколько пятизначных чисел можно составить из цифр числа 2345?
3. а) Сколько различных пятизначных чисел моно составить из цифр 1, 2, 5, 6, 7, 9, если каждую цифру можно использовать не более одного раза?
б) Номер паспорта содержит 6 цифр. Сколько таких номеров можно составить?
4. а) Каким числом способов можно рассадить 12 гостей на имеющихся 12 различных стульях?
б) На железнодорожной станции имеется 6 светофоров. Сколько может быть дано различных комбинаций сигналов, если каждый светофор имеет три состояния: «красный», «желтый», «зеленый»?
5. а) В отделении 10 солдат. Каким числом способов можно составить наряд из двух человек, если один из них должен быть назначен старшим?
б) Сколько различных чисел можно получить, переставляя цифры числа 1123353?
6. а) Сколькими способами можно составить расписание занятий на понедельник, если должно быть по одному уроку математики, истории, информатики, философии и психологии?
б) Сколькими способами можно составить новогодний подарок, который должен содержать 100 конфет, если в наличии имеется 15 сортов конфет?
7. а) Из 2 математиков и 10 экономистов должна быть составлена комиссия в составе 8 человек. Сколькими способами это можно сделать?
б) Сколько различных слов можно образовать, переставляя буквы слова
«студент»?
8. а) Сколькими способами можно составить наряд из 10 солдат, если в военной части числится 100 солдат?
б) Сколькими способами можно составить набор из 8 ручек, если
имеются ручки 3 цветов?
9. а) Сколькими способами можно составить трехцветный флаг, если имеется материал 5 различных цветов?
б) Сколько можно получить различных пятизначных чисел, вставляя
пропущенные цифры в число 34***9?
10. а) Сколько различных четырехбуквенных слов можно образовать из букв слова «улица», если каждую букву можно использовать не более одного раза?
б) В кондитерскую привезли печенье 6 сортов. Сколько различных
покупок из 2 сортов печенья можно сделать?
11. а) Сколькими способами можно выбрать из букв слова «цветы» 2 согласные буквы?
б) Сколько различных слов можно составить, вставляя пропущенные
буквы в слово «кра***на», если можно использовать 32 буквы русского
алфавита?
12. а) Сколькими способами можно распределить 10 путевок в санаторий между 90 работниками предприятия
б) Сколькими способами можно расставить на восьми клетках первой линии шахматной доски 2 ладьи, 2 коней, 2 слонов, ферзя и короля?
13. а) Из 12 солдат необходимо отправить четырех в разведку. Сколькими способами можно сделать выбор?
б) Номер удостоверения должен состоять из 10 цифр. Сколько таких номеров можно составить?
14. а) Сколько трехзначных чисел можно образовать из нечетных цифр, если каждую цифру моно использовать не более одного раза?
б) Сколькими способами можно купить 4 тетради в киоске, в котором имеется 5 видов тетрадей?
15. а) В книжном киоске продается 20 различных книг. Сколько можно сделать покупок, состоящих из трех книг?
б) Сколькими способами можно расставить на книжной полке в библиотеке 10 книг: 3 одинаковых сборника стихов, 4 одинаковых романа и 3 одинаковых детектива?
16. а) Сколько различных слов можно образовать, переставляя буквы слова «пирог»?
б) В цветочном магазине продаются розы 8 сортов. Сколькими способами можно составить букет из 5 цветов?
17. а) Сколькими способами можно выбрать 2 цифры из цифр числа 67345?
б) Сколько пятизначных чисел можно составить из цифр числа 245?
18. а) В магазине имеется 15 различных видов коробок конфет. Сколько можно сделать покупок, состоящих из трех различных коробок конфет?
б) Номер паспорта содержит 7 цифр. Сколько таких номеров можно составить?
19. а) Сколькими способами можно составить программу концерта, если концерт включает 10 номеров?
б) На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных комбинаций сигналов, если каждый светофор имеет два состояния: «красный» и «зеленый»?
20. а) В видеопрокате имеется 80 видеокассет. Сколькими способами можно взять в видеопрокате 4 видеокассеты?
б) Сколько различных чисел можно получить, переставляя цифры числа 23353?
21. а) Сколько различных трехбуквенных слов можно образовать из букв слова «кот», если каждую букву нельзя использовать более одного раза?
б) Сколькими способами можно составить новогодний подарок, который должен содержать 10 шоколадных фигурок, если в наличии имеются фигурки 15 сортов?
22. а) Сколькими способами можно распределить золотую, серебряную и бронзовую медали между 10 участниками соревнований?
б) Сколько различных слов можно образовать, переставляя буквы слова «банан»?
23. а) Сколькими способами можно составить список 10 факультетов вуза?
б) Сколькими способами можно составить набор из 25 карандашей, если имеются карандаши 10 цветов?
24. а) Сколько различных пятизначных чисел можно составить из цифр числа 987654, если каждую цифру можно использовать не более одного раза?
б) Сколько можно получить различных пятизначных чисел, вставляя пропущенные цифры в число 76**9?
25. а) Сколько различных танцевальных пар можно составить из 10 юношей и 10 девушек?
б) В кондитерскую привезли конфеты 10 сортов. Сколько различных покупок из 3 сортов конфет можно сделать?
26. а) Сколькими способами можно выбрать 3 гласных буквы из букв слова «теория»?
б) Сколько различных слов можно составить, вставляя пропущенные буквы в слово «ро**на», если можно использовать 32 буквы русского алфавита?
27. а) В киоске продаются тетради 7 видов. Сколькими способами можно купить в киоске 5 различных тетрадей?
б) Номер удостоверения должен состоять из 8 цифр. Сколько таких номеров можно составить?
28. а) Сколькими способами можно извлечь 3 фишки из полного набора домино?
б) Сколько различных слов можно составить, переставляя буквы слова «информатика»?
29. а) Сколько различных чисел можно образовать, переставляя цифры числа 5643?
б) Сколькими способами можно купить 5 обложек для книг в магазине, если в нем имеются обложки 3 видов?
30. а) На предприятии работает 30 сотрудников. В командировку необходимо направить 4 человек. Сколькими способами это можно сделать?
б) Сколько различных трехзначных чисел можно составить из цифр числа 567?
ЗАДАНИЕ 6. Решить задачу, используя классическое определение вероятности и формулы комбинаторики:
1. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
2. В коробке 6 красных и 7 синих ручек. Из коробки последовательно одна за другой извлекаются две ручки без возвращения в коробку. Найти вероятность того, что обе ручки окажутся красными.
3. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди взятых наудачу 7 деталей нет ни одной бракованной.
4. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «о», «п», «р», «с», «т», получится слово «спорт»?
5. Из 60 вопросов, включенных в экзамен, студент подготовил 50. Найти вероятность того, что из предложенных ему двух вопросов он знает оба.
6. Имеется 6 билетов в театр, 4 из которых - на места первого ряда. Найти вероятность того, что из трех наудачу взятых билета все окажутся на места первого ряда.
7. В коллекции 200 монет, из которых 25 монет восемнадцатого века. Какова вероятность того, что наудачу выбранные 2 монеты датированы восемнадцатым веком?
8. Телефонный номер состоит из пяти цифр. Найти вероятность того, что все цифры различны.
9. В коробке находится 4 красных и 6 зеленых карандашей. Из нее случайно выпали 3 карандаша. Найти вероятность того, что все они красные.
10. На собрании присутствует 30 женщин и 45 мужчин. По жребию выбирают делегацию из 10 человек. Найти вероятность того, что в составе делегации окажутся только мужчины.
11. Шеститомное собрание сочинений расположено на полке в случайном порядке. Найти вероятность того, что тома стоят в нужном порядке по возрастанию номеров слева направо.
12. Из букв слова «событие», составленного с помощью разрезной азбуки, извлекаются наудачу и складываются друг за другом в порядке их извлечения 3 карточки(буквы). Какова вероятность получить при этом слово «быт»?
13. Из пяти видов открыток, имеющихся в автомате, наудачу выбираются 3 открытки. Какова вероятность того, что все открытки будут разные?
14. Наудачу набирается семизначный номер телефона. Какова вероятность того, что этот номер равен 1234567?
15. В цветочном магазине продаются белые, желтые, розовые и красные розы. Какова вероятность того, что при покупке наудачу 3 роз все они будут белого цвета?
16. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
17. В группе 29 студентов, среди которых 6 спортсменов. По списку наудачу отобраны 6 студентов. Найти вероятность того, что отобраны все спортсмены.
18. В партии из 20 деталей 6 нестандартных. Найти вероятность того, что из взятых наудачу 3 деталей все окажутся нестандартными.
19. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «о», «п», «р», «с», получится слово «спор»?
20. Из 40 вопросов, включенных в экзамен, студент подготовил 30. Найти вероятность того, что из предложенных ему двух вопросов он знает оба.
21. Имеется 10 билетов в театр, 6 из которых - на места первого ряда. Найти вероятность того, что из двух наудачу взятых билета оба окажутся на места первого ряда.
22. В коллекции 100 монет, из которых 15 монет семнадцатого века. Какова вероятность того, что наудачу выбранные 3 монеты датированы семнадцатым веком?
23. Телефонный номер состоит из шести цифр. Найти вероятность того, что все цифры различны.
24. В коробке находится 5 красных и 8 зеленых карандашей. Из нее случайно выпали 4 карандаша. Найти вероятность того, что все они красные.
25. На собрании присутствует 20 женщин и 25 мужчин. По жребию выбирают делегацию из 7 человек. Найти вероятность того, что в составе делегации окажутся только мужчины.
26. Пятитомное собрание сочинений расположено на полке в случайном порядке. Найти вероятность того, что тома стоят в нужном порядке по возрастанию номеров слева направо.
27. Из букв слова «гипотеза», составленного с помощью разрезной азбуки, извлекаются наудачу и складываются друг за другом в порядке их извлечения 3 карточки(буквы). Какова вероятность получить при этом слово «газ»?
28. Из четырех видов открыток, имеющихся в автомате, наудачу выбираются 2 открытки. Какова вероятность того, что все открытки будут разные?
29. Наудачу набирается шестизначный номер телефона. Какова вероятность того, что этот номер равен 123456?
30. В цветочном магазине продаются белые, желтые, розовые и красные розы. Какова вероятность того, что при покупке наудачу 5 роз все они будут красного цвета?
СОДЕРЖАНИЕ
Введение…………………………………………………………………………...3
Требования к выполнению и оформлению контрольной работы……………...4
Литература ………………………………………………………………………..5
Методические рекомендации и разбор типовых задач…………………………6
Тема 1. Элементы теории множеств и математической логики……………6
Тема 2. Элементы аналитической геометрии и линейной алгебры………...8
Тема 3. Комбинаторика………………………………………………………12
Тема 4. Элементы теории вероятностей и математической статистики….14
Задания для контрольной работы………………………………………………17
Содержание………………………………………………………………………30