Чайковский филиал
Федерального государственного бюджетного
Образовательного учреждения высшего профессионального образования
"Пермский национальный исследовательский политехнический университет"
(ЧФ ПНИПУ)
Кафедра автоматизации, информационных и инженерных технологий
Термодинамика
Компьютерная лабораторная работа №3
“Изотермический и адиабатический процессы”
Теоретическая часть
Адиабатический процесс в идеальном газе
Особую роль в термодинамике имеют изотермический и адиабатический процессы.
Изотермический процесс, процесс, происходящий при постоянной температуре, называется изотермическим. Чтобы осуществить изотермический процесс, систему нужно поместить в термостат.
Адиабатический процесс, процесс, происходящий без теплообмена с окружающей средой. Чтобы осуществить адиабатический процесс, систему нужно изолировать адиабатической оболочкой, например, поместив её в термос или сосуд Дюара.
| термос |
| P, V, T |
| термостат |
| P, V, T0 |
| T0 |
| Рис. 1 |
| а) изотермическое сжатие-расширение |
| б) адиабатическое сжатие-расширение |
В случае, изотермического процесса теплообмен с окружающей средой (термостатом) максимален, а в случае адиабатического процесса он равен нулю, потому что термос препятствует этому.
Произведем сравнительный анализ обоих процессов, поместив цилиндр с поршнем в термос и термостат. Проведем мысленный эксперимент.
Эксперимент 1. Пусть поршень не закреплен. В обоих случаях, вследствие давления газа, поршень будет двигаться вверх, приобретая все большую кинетическую энергию. Следовательно, газ совершает работу над поршнем. Объем газа увеличивается, а давление уменьшается.
В случае адиабатического расширения эта работа (рис.1б) совершается за счет уменьшения внутренней энергии газа, поэтому его температура будет уменьшаться. Газ преобразует собственное тепло в работу.
В случае изотермического расширения (рис.1а), термостат не даст уменьшаться температуре газа, передовая ему некоторое количество теплоты. Следовательно, работа будет осуществляться за счет тепла получаемого от термостата, а не за счет внутренней энергии газа. Газ преобразует тепло термостата в работу.
Эксперимент 2. Будем перемещать поршень вниз, прикладывая некоторую силу и, следовательно, совершая работу. При этом в обоих случаях объем газа будет уменьшиться, а его давление расти.
В случае адиабатического сжатия (рис.1б) наша работа будет идти на увеличение внутренней энергии газа. Его температура будет расти.
В случае изотермического сжатия (рис.1а) термостат не даст нагреваться газу, отбирая от него избыточное тепло. Следовательно, совершаемая нами работа целиком будет преобразовано в тепло термостата.
Кроме того, поскольку, энергия термостата в отличие от энергии газа сколь угодно велика, следует ожидать, что при термодинамическом расширении давление будет подать быстрее, чем при его адиабатическом расширении.
Итак, посредствам мысленного эксперимента мы пришли к следующим выводам.
1. При адиабатическом изменении объема изменяется давление и температура газа. При изотермическом изменении объема, – только давление.
2. При адиабатическом расширении внутренняя энергия газа преобразуется в кинетическую энергию поршня посредством совершения работы газа над поршнем. При изотермическом расширении внутренняя энергия термостата преобразуется в кинетическую энергию поршня. Газ совершает работу, за счет энергии термостата.
3. При адиабатическом сжатии кинетическая энергия поршня преобразуется во внутреннюю энергию газа посредствам совершения работы над газом. При изотермическом сжатии кинетическая энергия поршня преобразуется во внутреннюю энергию термостата. Газ осуществляет теплопередачу внутренней энергии термостату.
4. В адиабатическом процесс изменение давления происходит быстрее, чем в изотермическом процессе
Для подтверждения правильности наших выводов нам необходимо: осуществить математическую формализацию обоих процессов, разработать их компьютерные модели и осуществить на них сравнительный эксперимент.
Математическая модель
Состояния идеального газа в обоих случаях выражается уравнением Клайперона – Менделеева
, (1)
где 
- количество молей газа,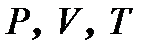 
- его давление, объем и температура газа, 
- газовая постоянная.
Пусть в обоих случаях в начальный момент времени газ имеет одно и тоже значение параметров 
.
Изотермический процесс осуществляется при одной и той же температуре газа равной температуре термостата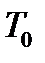 
, поэтому уравнения (1) будет иметь вид
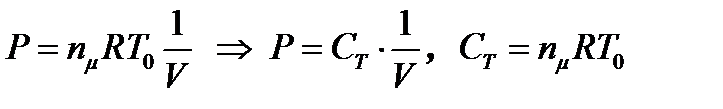. (2)
Уравнение адиабатического процесса
, (3)
где – показатель адиабаты, который для идеального газа равен 
.
Определим константу адиабаты, используя начальные условия. Согласно уравнению состояния (1)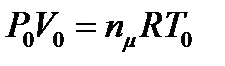 
, тогда
. (4)
Непосредственное вычисление константы представим компьютеру.
Запишем (2) в форме
. (5)
При осуществлении процессов (2) и (5) газ совершает работу, которую нам предстоит вычислить.
Работа, совершаемая идеальным газом
Работу газа в изотермическом и адиабатическом процессе можно вычислить двумя способами: численно интегрируя дифференциальное уравнение работы и используя аналитическое выражение.
Выполним численное интегрирование. Работа газа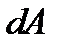 
при элементарном увеличении объема 
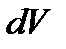равна
, (7)
где 
– давление газа.
При расширении газа от объёма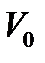 
до объёма 
, газ совершает работу
. (8)
Выражение (6) проинтегрируем численно. Будем передвигать поршень маленькими шажками, увеличивая объём на каждом шаге на величину 
. У нас получится ряд состояний
.
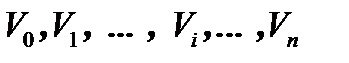На каждом шаге работа равна
, (9)
где 
– давление газа при давлении 
. Полная работа равна сумме работ (9), потому
. (10)
Ряд (10) предоставим считать компьютеру. Чем меньше мы будем брать шаг, тем точнее будет вычисляться интеграл (10).
Запишем выражение численного интегрирования (10) для адиабатического и изотермического процесса. Подставляя (2) и (5) пишем:
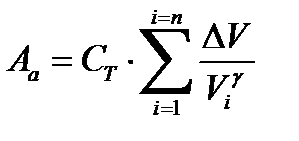– работа при адиабатическом расширении газа;
– работа при изотермическом расширении газа.
Интеграл (8) для адиабатического и изотермического процессов можно сосчитать аналитически, тогда
– работа при адиабатическом расширении газа;
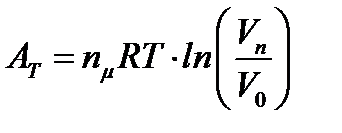– работа при изотермическом расширении газа.
Запишем полную математическую модель сравнительного анализа адиабатического и изотермического расширения газа.
Математическая модель
Практическая часть
Используя полученную математическую модель разработать компьютерную модель сравнительного анализа адиабатического и изотермического расширения-сжатия идеального газа. Начальные условия взять, согласно варианту (Таблица приложения). При этом, все единицы необходимо перевести в систему СИ:
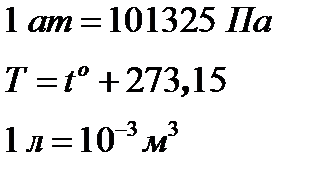
1. Написать программу, реализующую математическую модель (6)
2. Протестировать программу, используя начальные условия
3. Задавая линейное расширение или сжатие газа вывести графики адиабатического и изотермического процесса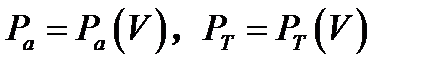 
. Выполнить анализ, накладывая графики, друг на друга.
4. Изменяя начальные значения температуры повторить результата п.3.
5. Дополнить программу операторами вычисления работы процессов численным интегрированием. Протестировать работу программы используя аналитическое выражение для интегралов работы.
6. Задавая линейное расширение или сжатие газа вывести графики работы адиабатического и изотермического процессов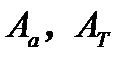 
. Выполнить анализ, накладывая графики, друг на друга.
7. Сделать выводы и написать отчет
8. Подготовится к защите выполненной работы
Вопросы и задания к защите
1. Какой процесс называется адиабатическим и изотермическим?
2. Запишите выражения адиабатического и изотермического процессов.
3. Что такое термостат и термос? Приведите примеры.
4. Вы снимаете показания с приборов регистрирующих протекание изотермического и адиабатического процессов. Как определить где какой процесс протекает
5. Даны графики адиабаты и изотермы одного одной и той же термодинамической системы при одинаковых начальных условиях, как отличить график адиабаты от изотермы.
6. Изобразить качественно графики адиабаты и изотермы одного и того же газа при одинаковых начальных условиях в координатах
, 
, 
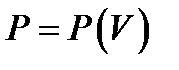7. Какая энергия преобразуется в адиабатическом и изотермическом процессах? Как она преобразуется?
8. Запишите на память аналитическое выражение работы идеального газа
в адиабатическом и изотермическом процессах
Пример выполнения работы
Сравнительный анализ адиабатического и изотермического процессов в идеальном газе
Математическая модель адиабатического и изотермического состояния идеального газа
(1)
(2)
В качестве начальных условий возьмем нормальные условия:
Составит расчетный блок компьютерной модели адиабатного расширения газа на языке Pascal ABC
//Адиабаты и изотермы идеального газа
tt:=0.00001; {шаг счета, равный шагу изменению объема}
{Начальные условия}
Nm:=1; {количество газа, моль}
Tk:=T0; {начальная температура}
V:=V0; {начальный объем}
PA:=P0; {начальное давление адиабатического процесса}
PT:=P0; {начальное давление изотермического процесса}
G:=5/3; {показатель адиабаты}
CA:=Exp(G*Ln(Nm*R0*Tk))/Exp((G-1)*Ln(PA));{константа адиабаты}
CT:=Nm*R0*Tk; {константа изотермы}
For i:=1 to 100000 do
begin
V:=V+tt;
PA:=CA*Exp((-G)*Ln(V));
PT:=CT/V;
SetPixel(X0+round(V*40*MasX),Y0-round(PA*40*MasY), clBlack);
SetPixel(X0+round(V*40*MasX),Y0-round(PT*40*MasY), clNavy);
end;
На рис. 1 приведены графики адиабатического и изотермического расширения газа при выбранных выше начальных условиях. Правильность работы программы тестируется начальными условиями.
Как видно из графиков, при адиабатическом процессе, давление спадает быстрее, чем при изотермическом процессе. Это соответствует результатам мысленного эксперимента.
Для расчета работы при адиабатическом и изотермическом процессе, дополним программу операторами вычисления работы
//Адиабаты и изотермы идеального газа
tt:=0.00001; {шаг счета равный шагу изменения объема}
{Начальные условия}
Nm:=1; {количество газа, моль}
Tk:=T0; {начальная температура}
V:=V0; {начальный объем}
PA:=P0; {начальное давление адиабатического процесса}
PT:=P0; {начальное давление изотермического процесса}
G:=5/3; {показатель адиабаты}
CA:=Exp(G*Ln(Nm*R0*Tk))/Exp((G-1)*Ln(PA));{константа адиабаты}
CT:=Nm*R0*Tk; {константа изотермы}
Aa:=0; {начальное значение работы адиабатического процесса}
At:=0; {начальное значение работы изотермического процесса}
For i:=1 to 100000 do
begin
V:=V+tt;
PA:=CA*Exp((-G)*Ln(V));
Aa:=Aa+PA*tt; {работа адиабатического процесса}
PT:=CT/V;
At:=At+PT*tt; {работа изотермического процесса}
{ SetPixel(X0+round(V*40*MasX),Y0-round(PA*40*MasY), clBlack);}
{ SetPixel(X0+round(V*40*MasX),Y0-round(PT*40*MasY), clNavy); }
SetPixel(X0+round(V*40*MasX1),Y0-round(Aa*40*MasY1), clPurple);
SetPixel(X0+round(V*40*MasX1),Y0-round(At*40*MasY1), clPurple);
end;
Результат работы программы представлен на рис. 2.
Для тестирования программы осуществим аналитическое вычисление работы, используя выражения(2). Поскольку при правильной работе программы графики численного и аналитического вычисления работы будут совпадать друг с другом, для визуального наблюдения сдвинем графики аналитического вычисления на три пиксела вдоль осей X и Y. Запишем программный блок.
For i:=1 to 100000 do
begin
V:=V+tt;
PA:=CA*Exp((-G)*Ln(V));
Aa:=Aa+PA*tt; {работа адиабатического процесса}
{работа адиабатического процесса, аналитическая формула для тестирования}
Aaa:=(Nm*R0*T0/(G-1))*(1-Exp((G-1)*Ln(V0/V)));
PT:=CT/V;
At:=At+PT*tt; {работа изотермического процесса}
{работа изотермического процесса, аналитическая формула для тестирования}
Ata:=Nm*R0*T0*Ln(V/V0);
{ SetPixel(X0+round(V*40*MasX),Y0-round(PA*40*MasY), clBlack);}
{ SetPixel(X0+round(V*40*MasX),Y0-round(PT*40*MasY), clNavy); }
SetPixel(X0+round(V*40*MasX1),Y0-round(Aa*40*MasY1), clPurple);
SetPixel(X0+round(V*40*MasX1),Y0-round(At*40*MasY1), clPurple);
{графики тестирования, сдвинуты на три пиксела}
SetPixel(X0+round(V*40*MasX1+3),Y0-round(Aaa*40*MasY1+3), clRed);
SetPixel(X0+round(V*40*MasX1),Y0-round(Ata*40*MasY1), clRed);
end;
Результат тестирования программы представлен на рис. 3. Таким образом, при отсутствии сдвига, вычисленные и тестирующие графики совпадают друг с другом.
Сводная картина графиков обоих процессов приведена на рис. 4.
| Рис. 1. |
| Рис. 2. |
| Рис.3. |
| Рис.4. |