Всякий непериодический сигнал можно рассматривать как периодический, период изменения которого равен бесконечности.
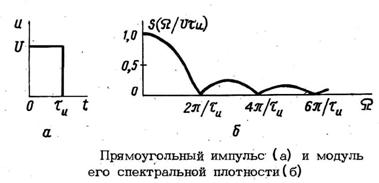
При увеличении периода следования сигнала и постоянной длительности импульса появляются новые спектральные составляющие (спектральные линии становятся гуще), амплитуды всех гармоник уменьшаются, а ширина лепестков остается постоянной. И при Т ®¥, непериодическое колебание можно рассматривать как сумму бесконечно большого числа бесконечно малых по амплитуде гармонических колебаний, частоты которых расположены бесконечно близко друг к другу и заполняют в общем случае всю шкалу частот. Другими словами, в любой бесконечно узкой полосе частот имеется гармоническое колебание бесконечно малой амплитуды.
Таким образом, спектр непериодического сигнала является непрерывным или сплошным и описывается интегралом Фурье.
Поскольку речь идет о бесконечно малых амплитудах, понятие спектра амплитуд для непериодического сигнала лишено смысла и заменяется понятием спектральной плотности амплитуд размерностью [ амплитуда/Гц ], которая указывает на удельный вес бесконечно малой амплитуды колебания в любой бесконечно узкой полосе частот.
Для построения графика спектральной плотности амплитуд непериодического сигнала теперь необходимо откладывать на спектральных диаграммах не сами амплитуды спектральных составляющих, а их относительные значения, определяемые как отношение амплитуды соответствующей гармоники к постоянной составляющей или к амплитуде первой гармоники, если постоянная составляющая отсутствует.
Если непериодическая функция удовлетворяет условиям Дирихле и абсолютно интегрируема, т. е.:
то она может быть представлена интегралами Фурье:
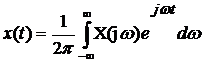, (8)
(9)
где: 
Функция Х (jw) – есть энергия сигнала, приходящаяся на 1 Гц при текущей частоте w. Иными словами Х (jw) является спектральной плотностью энергии сигнала х (t).
Формулы (8) и (9) описывают соответственно обратное и прямое преобразования Фурье непериодического сигнала и позволяют найти сигнал х (t), если задана спектральная плотность, или найти спектральную плотность, соответствующую сигналу х (t).
Из сравнения формул (6) и (9) следует, что огибающая сплошного спектра непериодического сигнала и огибающая линейчатого спектра такого же, но периодического сигнала совпадают по форме и отличаются только масштабом:
(10)
Таким образом, для вычисления амплитуды любой гармоники периодического сигнала достаточно вычислить амплитудную характеристику Х(jω) исходного сигнала, взять ее значение на частоте искомой гармоники 
и умножить на 2/Т.
Для непериодического сигнала х (t) интеграл:
определяет энергию, выделяемую этим сигналом на сопротивлении величиной в 1 Ом. Энергия связана со спектральной плотностью следующим соотношением:
(11)
Функция 
есть энергия сигнала, приходящаяся на 1 Гц при текущей частоте ω. Иными словами, является спектральной плотностью энергии сигнала х (t). Вид этой функции позволяет судить о распределении энергии в спектре непериодического колебания и поэтому формула (11) может быть использована для выбора полосы пропускания электрической цепи, обеспечивающей достаточно полное использование энергии сигнала.