Уравнения состояния линейных систем. Управляемость и наблюдаемость. Идентификаторы (наблюдатели) состояния.
Тема 7. Нелинейные системы автоматического регулирования
Виды и особенности нелинейных схем. Автоколебания, методы точечных преобразований и припасовывания. Методы гармонического баланса. Устойчивость нелинейных систем.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 1
Дифференциальные уравнения, передаточные функции и характеристики элементов и систем автоматического регулирования. Устойчивость непрерывных линейных систем автоматического регулирования.
3.1. Построить частотные характеристики элементарных звеньев для соответствующего варианта, заданных передаточной функцией:
| Передаточная функция | Вариант | Вариант | ||
| № | Данные | № | Данные | |
| T =0.25 c | T =0.05 c | ||
| k = 2; T = 0.5c; x=0.1 | k = 10; T = 0.2c; x=1 | ||
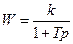
| k = 5; T = 0.6c | k = 20; T = 0.08c | ||
| k = 20; T = 0.25c; x=0.2 | k = 10; T = 0.4c; x=0.5 | ||
| k = 15 | k = 12 | ||
| k = 4; T = 0.1c; x=0.3 | k =16; T = 0.75c; x=0.4 | ||
| k = 10; T = 0.5c | k = 18 T = 0.25c |
| Передаточная функция | Вариант | Вариант | ||
| № | Данные | № | Данные | |
| k = 14; T = 0.8c | k = 20; T = 2.5c | ||
| k = 25; W=5c-1 | k = 12; W=10c-1 | ||
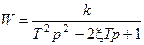
| k = 12; T = 0.25c; x=0.4 | k = 25; T = 1c; x=0.05 | ||
| k = 8; T = 0.07c | k = 16; T = 0.05c | ||
| k = 15 | k = 25 | ||
| k = 12; T = 0.15c; x=0.6 | k = 6; T = 0.25c; x=0.4 | ||
| k = 25 | k = 4 |
3.2. Построить логарифмические амплитудную 
и фазовую 
характеристики звена, заданного передаточной функцией
.
Характеристики строятся для двух пар параметров, т.е. для случая К=К1, Т=Т1 и К=К2, Т=Т2 в соответствии с вариантом. Данные представлены в табл.1.1, 1.2.
Таблица 1.1
| № | |||||||||||||
| К1, с-1 | |||||||||||||
| Т1, мс | 2,5 | 0,2 | |||||||||||
| К2, с-1 | |||||||||||||
| Т2, мс |
Таблица 1.2
| № | |||||||||||||
| К1, с-1 | |||||||||||||
| Т1, мс | 2,5 | 0,2 | |||||||||||
| К2, с-1 | |||||||||||||
| Т2, мс |
3.3. Определить, используя критерий Гурвица, устойчивость замкнутой системы автоматического регулирования по передаточной функции разомкнутой системы регулирования W(p) в соответствии с вариантом:
| Передаточная функция | Вариант | Вариант | ||
| № | Данные | № | Данные | |
| k = 25; T1 = 10 мc; T2 = 5 мc | k = 10; T1 = 8 мc; T2 = 4 мc | ||
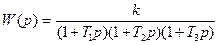
| k = 35; T1 = 8 мc; T2 = 10 мc; T3 = 4 мc | k = 25; T1 = 18 мc; T2 = 10 мc; T3 = 6 мc | ||
|  ,  , 
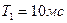| k = 40; T1 = 25 мc; T2 = 2 мc | ||
| k = 24; T1 = 7 мc; T2 = 15 мc; T3 = 4 мc | k = 20; T1 = 6 мc; T2 = 10 мc; T3 = 2 мc | ||
|  ,  , 
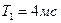| k = 25; T 1= 1 мc; x=0.05 | ||
|
|  ,  , 
| k = 16; T1 = 20 мc; T2 = 4 мc | ||
|
|  ,  , 
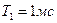| k = 10; T1 = 2 мc; T2 = 4 мc; T3 = 50 мc | ||
|  ,  , 
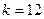| k = 20; T 1= 10мc; x=0.1 | ||
| ,  , 
| k = 25; T1 = 10мc; T2 = 5мc | ||
|
|  ,  , 
| k = 10; T1 = 15мc; T2 = 8мc | ||
|
| k = 30; T 1= 8мc; x=0.25 | k = 20; T 1= 10мc; x=0.08 | ||
|
| k = 35; T1 = 25мc; T2 = 5мc | k = 24; T1 = 16мc; T2 = 8мc | ||
|
| k = 15; T1 = 8мc; T2 = 12мc; T3 = 40мc | k = 50; T1 = 20мc; T2 = 40мc; T3 = 5мc | ||
| k = 28; T1 = 25мc; T2 = 10мc | k = 15; T1 = 12мc; T2 = 25мc |
3.4. Исследовать устойчивость одноконтурной системы автоматического регулирования с помощью логарифмических амплитудных и фазовых частотных характеристик, если передаточная функция разомкнутой системы
,
где K, Т1, Т2, Т3, Т4 определены в табл.2 для соответствующих вариантов.
Таблица 2
| № | |||||||||||||
| К | |||||||||||||
| Т1, с | 1,1 | 1,5 | 1,2 | 0,9 | 1,6 | 1,4 | 1,9 | 2,2 | 0,5 | 0,4 | 2,5 | ||
| Т2, с | 0,06 | 0,05 | 0,08 | 0,07 | 0,01 | 0,02 | 0,06 | 0,01 | 0,06 | 0,03 | 0,05 | 0,8 | 0,06 |
| Т3, с | 0,01 | 0,01 | 0,02 | 0,03 | 0,02 | 0,9 | 0,9 | 1,1 | 0,09 | 0,01 | 0,08 | 0,04 | 0,07 |
| Т4, с | 0,9 | 0,3 | 0,5 | 0,8 | 0,7 | 0,01 | 0,08 | 0,07 | 0,08 | 0,09 | 0,01 | 0,05 | 0,2 |
| № | |||||||||||||
| К | |||||||||||||
| Т1, с | 0,1 | 0,3 | 1,5 | 0,12 | 0,09 | 1,6 | 0,25 | 0,2 | 2,0 | 0,5 | 0,6 | 2,5 | 0,1 |
| Т2, с | 0,6 | 0,5 | 0,8 | 0,07 | 0,1 | 0,2 | 0,6 | 0,1 | 0,06 | 0,3 | 0,15 | 0,08 | 0,05 |
| Т3, с | 0,01 | 0,01 | 0,08 | 0,3 | 0,02 | 0,09 | 0,8 | 0,01 | 0,6 | 0,05 | 0,8 | 0,4 | 0,7 |
| Т4, с | 0,09 | 0,03 | 0,05 | 0,08 | 0,07 | 0,1 | 0,08 | 0,04 | 0,05 | 0,08 | 0,25 | 0,5 | 0,09 |
КОНТРОЛЬНОЕ ЗАДАНИЕ №2
Области устойчивости. Исследование динамической точности систем автоматического регулирования.
4.1. Построить область устойчивости по параметрам Т1 и К1, пользуясь критерием устойчивости Гурвица. Задана передаточная функция разомкнутой системы
,
Т2 и Т3 определены в соответствии с вариантом в табл.3.
Таблица 3
| № | |||||||||||||
| Т1, с | 1,1 | 1,5 | 1,2 | 0,9 | 1,6 | 1,4 | 1,9 | 2,2 | 0,5 | 0,4 | 2,5 | ||
| Т2, с | 0,06 | 0,05 | 0,08 | 0,07 | 0,01 | 0,02 | 0,06 | 0,01 | 0,06 | 0,03 | 0,05 | 0,8 | 0,06 |
| № | |||||||||||||
| Т1, с | 0,1 | 0,3 | 1,5 | 0,12 | 0,09 | 1,6 | 0,25 | 0,2 | 2,0 | 0,5 | 0,6 | 2,5 | 0,1 |
| Т2, с | 0,6 | 0,5 | 0,8 | 0,07 | 0,1 | 0,2 | 0,6 | 0,1 | 0,06 | 0,3 | 0,15 | 0,08 | 0,05 |
4.2. Определить по передаточной функции разомкнутой системы автоматического регулирования в установившемся состоянии коэффициенты ошибок С0, С1, С2, С3 в соответствии с вариантом (табл. 4):
Таблица 4
1)  ;
| 14)  ;
|
2)  ;
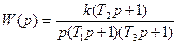| 15)  ;
|
3)  ;
| 16)  ;
|
4)  ;
| 17)  ;
|
5)  ;
| 18)  ;
|
6)  ;
| 19)  .
|
7)  ;
| 20)  ;
|
8)  ;
| 21)  ;
|
9)  ;
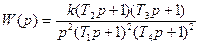| 22)  ;
|
10)  .
| 23) ;
|
11)  ;
| 24)  ;
|
| 12) ;
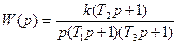| 25) ;
|
| 13) ;
| 26)  ;
|
4.3. Найти закон движения для замкнутой следящей системы с передаточной функцией Ф(р) при задающем воздействии в виде ступенчатой функции g0(t) и при начальных условиях y(0)=y0 и y`(0)=0 в соответствии с вариантом (табл.6)
Таблица 6
1)  ;
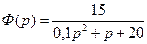| 14)  ;
|
2)  ;
| 15)  ;
|
3)  ;
| 16)  ;
|
4)  ;
| 17)  ;
|
5)  ;
| 18) ;
|
6)  ;
| 19)  ;
|
7)  ;
| 20)  ;
|
8)  ;
| 21) ;
|
9)  ;
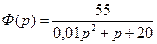| 22)  ;
|
10)  .
| 23)  .
|
| 11)
| 24)
|
12)  ;
| 25)  ;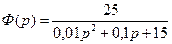
|
| 13) ;
| 126) ;
|
КОНТРОЛЬНОЕ ЗАДАНИЕ № 3
Метод фазовой плоскости. Метод гармонической линеаризации. Метод функции Ляпунова.
5.1. Построить фазовый портрет линейной системы, имеющей передаточную функцию для соответствующего варианта:
1) 
, Т1>0, T2>0;
2) , Т1>0, T2<0;
3) , Т1<0, T2<0;
4) 
;
5) 
, корни комплексные с отрицательной вещественной частью;
6) , корни комплексные с положительной вещественной частью;
7) 
, Т>0;
8) 
, Т<0;
9) , Т1<0, T2>0;
10) , Т1>0, T2>0;
Для построения фазового портрета использовать метод изоклин.
5.2. Построить траекторию изображающей точки на фазовой плоскости для системы, схема которой представлена на рис.3, с нелинейностью F(x), изображенной на рис.4, в соответствии с вариантом.
g x y
F(x) 
 |
Рис.3. Структурная схема системы
5.3. Определить коэффициенты гармонической линеаризации следующих нелинейных звеньев в соответствии с вариантом на рис.5.
5.4. Найти параметры автоколебаний и оценить их устойчивость для системы, структурная схема которой изображена на рис.6. Данные представлены в табл.7.
| № | ||||||||||||
| Т1, с | 0,1 | 0,2 | 0,5 | 0,3 | 0,6 | 0,2 | 0,5 | 0,4 | 0,7 | 0,8 | 0,06 | 0,02 |
| Т2, с | 0,03 | 0,1 | 0,09 | 0,05 | 0,1 | 0,7 | 0,08 | 0,3 | 0,1 | 0,2 | 0,01 | 0,07 |
| k | ||||||||||||
| b | ||||||||||||
| c |
Таблица 7
| № | ||||||||||||
| Т1, с | 0,01 | 0,2 | 0,05 | 0,3 | 0,06 | 0,2 | 0,05 | 0,4 | 0,07 | 0,8 | 0,01 | 0,2 |
| Т2, с | 0,03 | 0,01 | 0,09 | 0,5 | 0,1 | 0,07 | 0,08 | 0,03 | 0,1 | 0,02 | 0,3 | 0,1 |
| k | ||||||||||||
| b | ||||||||||||
| c |
Нелинейные алгебраические уравнения решать с использованием приближенных методов.
F(x) F(x)
a
-b
x b x
-a
4.1 4.2
F(x) F(x)
a a
b b
-b x -b x
-a -a
4.3 4.4
F(x) F(x)
a 2b
-b
2b x x
-a
4.5 4.6
F(x) F(x)
a a
b x b x
-a
4.7 4.8
F(x) F(x)
a
-2b
b x b x
-a
4.9 4.10
Рис.4. Статические характеристики нелинейных звеньев
F(x) F(x)
a a
-b
x b x
-a -a
5.1 5.2
F(x) F(x)
a
b
-b x x
-a
5.3 5.4
F(x) F(x)
x x
5.5 5.6
F(x) F(x)
x x
5.7 5.8
F(x) F(x)
x x
5.9 5.10
Рис.5. Статические характеристики нелинейных звеньев
ЛИТЕРАТУРА
1. Бесекерский В.А., Попов Е.П. Теория системы автоматического регулирования. – 2-е изд., перераб. и доп. – М.: Наука, 1972. – 768с.
2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1978. – 256с.
3. Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. Ч.1.Теория линейных систем автоматического управления /Н.А, Бабанов, А.А. Воронов, А.А. Воронова и др.; Под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1986. – 367с.
4. Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. Ч.П. Теория нелинейных и специальных систем автоматического управления /А.А. Воронов, О.П. Ким, В.М. Лохим и др.; Под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1986. – 504с.
5. Попов Е.В. Теория нелинейных систем автоматического регулирования и управления. – М.: Наука, 1979. – 256с.
6. Юревич Е.И. Теория автоматического регулирования: Учебник для студентов высш. техн. учебн. заведений. 2-е изд., перераб. и доп. – Л.: Энергия, 1975. – 416с.
7. Топчеев Ю.И., Цыпляков А.П. Задачник по теории автоматического регулирования: Учебное пособие для вузов. – М.: Машиностроение, 1977. – 592с.
8. Сборник задач по теории автоматического регулирования и управления /Под ред. В.А. Бесекерского. – 5-е изд., перераб. и доп. – М.: Наука, 1978. – 512с.
9. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – 2-е изд., перераб. и доп. – М.: Машиностроение, 1982. – 504с.
10. Математические основы теории автоматического регулирования. В
2-х ч. Ч.1. /Под ред. Б.К. Чемоданова. 2-е изд., доп. – М.: Высшая школа, 1977. – 366с.
11. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). – М.: Наука, 1978. – 832с.
12. Теория автоматического управления: Учеб. пособие для вузов /Под ред. А.С. Шаталова. – М.: Высшая школа, 1977. – 448с.