Точечные оценки
Приближенное, случайное значение параметров распределения называют статистической оценкой.
Точечной называют оценку, которая определяется одним числом.
Точечной оценкой математического ожидания служит выборочная средняя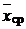 
, которой называют среднее арифметическое значений выборки.
Если все значения выборки различны, то
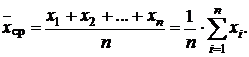
Для статистического ряда
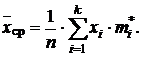
Для интервального статистического ряда
где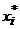 
− середина интервала; k − количество интервалов.
Для характеристики рассеивания выборочных значений относительно выборочного среднего, т.е. для оценки дисперсии, вводится понятие выборочной дисперсии.
Выборочной дисперсией D в называется среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего.
Если все значения выборки различны, то
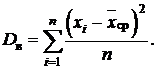
Если значения выборки имеют соответствующие частоты, то
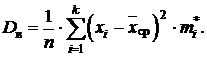
Если выборка представлена интервальным статистическим рядом, то
Выборочным средним квадратичным отклонением называют арифметический квадратный корень из выборочной дисперсии:
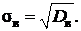
Коэффициент вариации n это значение, являющееся мерой относительной изменчивости случайной величины, вычисляют по формуле
или в процентах
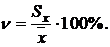
Та из выборок имеет большее рассеяние, у которой вариация больше.
Состоятельнойоценка ã называется статистическая оценка, если вероятность того, что отклонение оценки ã от истинного значения параметра a, будет меньше ε, равна единице, т.е. P (| ã – a|< ε) = 1при n→∞.
Несмещеннойоценкой ã называетсяоценка, для которой математическое ожидание оценки совпадает с ее истинным значением:
M [ ã ] = a.
Эффективнойоценкой ã называется, если она при одних и тех же объемах выборки обладает наименьшей дисперсией: D [ ã ]минимальна.
На практике не всегда удается удовлетворить этим требованиям.
Выборочная средняя 
является несмещенной оценкой, а выборочная дисперсия D в – смещенной оценкой. Чтобы «исправить» выборочную дисперсию, ее следует умножить на дробь 
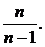
На практике используют более удобную формулу для вычисления несмещенной выборочной дисперсии для статистического ряда:
Для интервального статистического ряда:
Здесь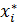 
- середина каждого интервала.
Несмещенное выборочное среднее квадратичное отклонение: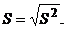 
Интервальные оценки
Доверительной вероятностью (надежностью) оценки ã параметра a называется вероятность β, с которой оценивается неравенство | a − ã |<ε.
Доверительную вероятность β назначают достаточно большой (0,9; 0,95; 0,99) такой, чтобы событие с вероятностью β можно считать практически достоверным. Затем находят такое значение ε, для которого
P (| a − ã |<ε)= β.
В этом случае диапазон возможных значений ошибки, возникающих при замене параметра a на оценку ã, будет ±ε.Большие по абсолютной величине ошибки будут появляться только с малой вероятностью α = 1 − β, которую называют вероятностью риска или уровнем значимости.
Неравенство | a − ã |<εможно записать в виде
− ε <a − ã < εили ã − ε <a< ã + ε.
Доверительным интервалом называется интервал (ã − ε; ã + ε), в который попадает неизвестный параметр a с заданной надежностью β. Доверительный интервал также можно рассматривать как интервал значений параметра a, совместимых с опытными данными и не противоречащих им.
Доверительный интервал для оценки математического ожидания нормального распределения
Пусть по результатам эксперимента получена оценка математического ожидания 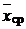. При нормальном распределении величины X случайная величина
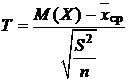(5.10.1)
подчиняется распределению Стьюдента. Значения этого распределения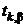 
зависят от числа степеней свободы k =n – 1и доверительной вероятности βи находятся по таблицам.
Выбираютинтервал симметричный относительно оценки 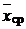. Половину длины интервала обозначим 
. Величину следует подбирать так, чтобы выполнялось условие
(5.10.2)
Пользуясь обозначением (5.10.1) и проводя определенные преобразования, перейдем к двойному неравенству:
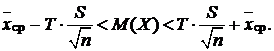
Таким образом, если выбрать конкретное значение величины распределения Стьюдента 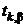, то доверительный интервал для математического ожидания принимает вид:
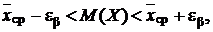(5.10.3)
где 