Задания для самостоятельной работы
Задача 1. В корзине лежат 5 кубиков разного цвета. Сколько цветовых комбинаций можно из них составить, если кубики выкладывать в одну линию?
Ответ: 120.
Решение:
Количество перестановок Рn=N!
N! Факториал – функция натурального числа, которая равна произведению всех натуральных чисел от 1 до N
N!=1*2*3*4*….*N
3!=1*2*3
10!=1*2*3*4*5*6*7*8*9*10
Для данного случая количество перестановок (т.е. различных последовательностей из 5 разных цветов Р=5!=1*2*3*4*5=120
Задача 2. Сколько существует перестановок из букв слова «фонарь», в которых буква «р» на первом месте, а буква «о» - в конце слова?
Ответ: 24.
Решение:
В данном случае первая и последняя буква остаются на месте, следовательно переставляем только 4 средних буквы. Количество перестановок З=4!=1*2*3*4=24
Задача 3. Сколько 3- буквенных «слов» можно составить из букв слова «ВОЛАН»? Словом считается любая последовательность букв.
Ответ: 60.
Решение: в данном случае нам нужно найти число размещений из 5 по 3.
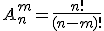
Т.е число размещений из n=5 по m=3
n!=5!=1*2*3*4*5=120
(n-m)!=(5-3)!=2!=1*2=2
А=120/2=60
Задача 4. В ящике 2 шара белого цвета, 2 шара синего цвета и 1 шар желтого цвета. Сколькими способами можно выбрать 3 шара?
Ответ: 10.
Решение. Мне почему-то кажется что существует только 5 способов выбрать 3 шара:
2 белых, 1 синий
2 белых, 1 желтый
1 белый, 1 синий, 1 желтый
1 белый, 2 синих
2 синих, 1 желтый
Может быть я ошибаюсь.
Для решения задач 5-7 достаточно знать следующее (хотя мне кажется, это понятно и без всякой теории):
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Случайные события А и В называется несовместными, если при данном испытании появление одного из них исключает появление другого события. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, студент одновременно едет на занятие и сдает экзамен, число иррациональное и четное.
Задача 5. Являются ли события А и В совместными, если событие
А – «Выбивание менее 4 очков при стрельбе по мишени», событие В – «Выбивание нечетного числа очков при стрельбе по мишени»?
Ответ: да.
Задача 6. Являются ли события А и В совместными, если событие
А – «Появление 6 очков при бросании игральной кости», событие В – «Появление четного числа при бросании игральной кости»
Ответ: да.
Задача 7. Являются ли события А и В совместными, если событие
А – «Выбор на экзамене билета с номером 13», событие В – «Выбор на экзамене билета с четным номером»
Ответ: нет.
Вероятностью события А называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех элементарных исходов:
 .
|
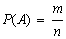Задача 8. В ящике лежит 10 шаров. Из них 3 белых шара, 5 желтых шаров и 2 красных шара. Какова вероятность вынуть из урны красный шар?
Ответ: 1/5=0,2.
Решение: вероятность для данной ситуации равна 2/10=1/5
Задача 9. В коробке лежит 10 конфет. Из них 3 карамели, 5 конфет «Мишка на севере» и 2 конфеты «Трюфель». Какова вероятность наугад вынуть из коробки шоколадную конфету?
Ответ: 7/10=0,7
Решение: вероятность для данной ситуации равна 7/10
Задача 10. В коробке лежит 10 конфет. Из них 3 карамели, 5 конфет «Мишка на севере» и 2 конфеты «Трюфель». Какова вероятность наугад вынуть из коробки две шоколадные конфеты?
Ответ: 7/15
Задача 11. В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
Ответ: р=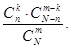 
Решение: Наше событие заключается в следующем: выбрали К стандартных деталей из m возможных (т.е. m всего стандартных деталей) и выбрали (m-k) (это оставшаяся часть деталей из m деталей k стандартных и (m-k) нестандартных). Общее количество нестандартных деталей (N-n)
вероятность данного события равна: вероятность того, что из n стандартных деталей выберут именно k Сnk её мы умножаем, на вероятность того, что среди
Делим на число сочетаний из N по m. Т.к. таких сочетаний может быть определенное количество, соответственно и вероятность уменьшается в это количество раз.
Задача 13. В группе 15 студентов, среди которых 6 отличников. По списку наудачу отобраны 10 студентов. Найти вероятность того, что среди отобранных студентов 4 отличника.
Ответ: 60/143=0,42.
Решение; р=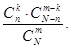
Задача аналогична всего N=15, отличников n=6, отобрано m=10 человек. Какова вероятность, что среди отобранных студентов именно k=4 отличника.
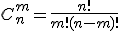формула числа сочетаний
Задача 14. Подбрасывается два игральных кубика, отмечается число очков на верхней грани каждого кубика. Найти вероятность того, что на обоих кубиках выпало число очков, большее двух.
Ответ: 4/9=0,444.
Решение:
Вероятность того что на одном кубике будет число очков больше 2х. У кубика всего 6 граней, и 6 чисел может оказаться на верхней грани, т.е. возможных исходов – 6. благоприятных исходов – 4. Т.е. четыре числа больше 2х.
Р=4/6=2/3
Вероятность того, что на обоих кубиках будет такое число равно произведению вероятностей. Т.к. эти события независимые. Т.е вероятности второго события и первого не связаны. Поэтому находим произведение вероятностей
(2/3) *(2/3) = 4/9
Задача 15. Игральный кубик бросают два раза. Какова вероятность того, что на верхней грани два раза выпадет четное число очков, большее 2?
Ответ: 1/9
Два независимых события. Вероятность равна произведению вероятностей. Вероятность того, что на верхней грани выпадет четное число больше 2х 2/6=1/3
Вероятность двух событий (1/2)*(1/3)=1/9
Задача 16. Стрелок стреляет по мишени дважды. Вероятность попадания в мишень 0,7. Какова вероятность того, что стрелок хотя бы один раз попал в мишень?
Ответ: 0,91.
События независимы. Вероятность появления хотя бы одного из двух независимых событий в совокупности равна разности между единицей и произведением вероятностей противоположных событий. (Противоположное событие – не попал в мишень)
Вероятность того, что он не попал в мишень =1-0,7=0,3
Вероятность того, что он дважды не попал в мишень 0,3*0,3=0,09
Равна произведению вероятностей, т.к. эти события независимы.
Вероятность того, что он хотя бы раз попал равна 1-вероятность того, что он ни разу не попал.
1-0,09=0,91