Отчет
По индивидуальному заданию
по дисциплине
«Теория принятия решений»
Вариант № 2
Выполнил:
студент группы Ктбо3-3
Асадов В.В.
______________________
«____» __________ 2017 г.
Проверил:
к.т.н., доцент кафедры МОП ЭВМ
Родзин С.И.
______________________
«____» __________ 2017 г.
Оценка:
Таганрог 2017
СОДЕРЖАНИЕ
ЦЕЛЬ РАБОТЫ.. 2
1 Часть первая. 3
1.1 Задача принятия решения методами теории игр. 3
1.2 Листинг для решения игры путём сведения игровой задачи к паре двойственных задач линейного программирования. 10
1.3 Задача принятия решения методами теории статистических решений 22
2 Часть вторая. Задача принятия решения методами анализа иерархии, свертки критериев. 28
3 Часть третья. Задача группового принятия решения. 39
ЗАКЛЮЧЕНИЕ. 45
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.. 47
Цель индивидуальной работы:
Целью данной индивидуальной работы является закрепление теоретических и практических знаний, полученных на занятиях по дисциплине «теория принятия решений», а именно методы теории игр, статистических решений, анализ иерархий, свёртки критериев, процедуры решения задач группового принятия решений.
Часть первая
Индивидуальное задание состоит из 3 частей и программной реализации.
В первой части будут рассмотрены задачи принятия решения методами теории игр и методами статистических решений. Они служат для поиска оптимальной стратегии или стратегий в игре двух лиц. В методе статистических решений вторым лицом выступает природа.
Решение задачи методами теории игр.
Постановка задачи:
Задана платёжная матрица выигрыша игрока в антагонистической игре двух лиц с нулевой суммой (таблица 1).
| 
| 
| 
| 
| |
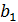
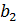
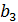
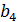
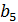
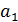
| -3 | ||||
| |||||
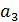
| -3 | ||||
| |||||
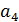
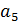
| -1 | -4 | |||
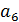
| -3 | ||||
|
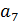
Таблица 1. Матрица выигрыша первого игрока.
Найти:
а) нижнюю и верхнюю чистую цену игры;
б)решение игры методом последовательных приближений. Определить, являются ли оптимальными полученные в приближенном решении стратегии игроков;
в) решение игры (цену игры и оптимальные стратегии игроков) точным методом – путём сведения игровой задачи к паре двойственных задач линейного программирования (для решения составить программу);
г) попробовать упростить задачу путём исключения доминируемых стратегий обоих игроков. Если хотя бы у одного из игроков останется 2 активных стратегии, то решить задачу графическим методом.
Решение:
а) Найти нижнюю и верхнюю чистую цену игры:
Защитная чистая стратегия первого игрока выбирается по максиминному критерию, при этом его максимальный гарантированный выигрыш равен нижней цене игры:
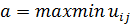
Нижняя цена игры a — это максимальный выигрыш, который может гарантировать себе первый игрок, в игре против разумного противника, если на протяжении всей игры будет использовать одну и только одну стратегию.
Найдем в каждой строке платежной матрицы минимальный элемент и запишем его в дополнительный столбец α (Таблица 2). Затем найдем максимальный элемент столбца α (отмечен звездочкой). Это и будет нижняя цена игры.
Защитная чистая стратегия второго игрока выбирается по минимаксному критерию, при этом его минимальный проигрыш равен верхней цене игры:
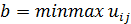
Верхняя цена игры b — это минимальный проигрыш, который может гарантировать себе второй игрок, в игре против разумного противника, если на протяжении всей игры он будет использовать одну и только одну стратегию.
Найдем в каждом столбце платежной матрицы максимальный элемент и запишем его в дополнительную строку β снизу (Таблица 2). Затем найдем минимальный элемент строки β (отмечен звездочкой). Это и будет верхняя цена игры.
|
|
|
|
|
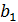
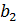
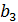
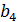
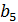
| α | |
|
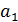
| -3 | -3 | ||||
|
| ||||||
|
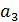
| -3 | -3 | ||||
|
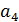
| 3* | |||||
|
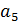
| -1 | -4 | -4 | |||
|
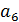
| -3 | -3 | ||||
|
| ||||||
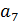
| β | 4* | 4* | 4* | 4* | 4* |
Таблица 2. Максимин и минимакс.
Таким образом, нижняя цена игры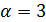 
, а верхняя цена игры 
.
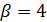Ситуация, когда каждый из игроков, подозревая о том, что его противник будет применять защитную стратегию, испытывает соблазн отойти от своей защитной стратегии, называется неуравновешенностью защитных стратегий [2].
Пара защитных стратегий будет уравновешенной тогда, когда нижняя и верхняя цена игры равны. Тогда если один из игроков использует стратегию уравновешенной пары, то второму ничего не остается, как также воспользоваться второй стратегией из этой пары, чтобы получить наименьший гарантированный проигрыш. Такая ситуация называется седловой точкой: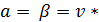 
. В задаче седловых точек не наблюдается, так как равенство не выполняется.
б) найти решение игры методом последовательных приближений. Определить оптимальность полученных в приближенном решении стратегий игроков:
Для анализа антагонистической игры с некоторой платежной матрицей этим методом строится итерационный процесс (Таблица 3), каждый шаг которого - розыгрыш игры. В первом розыгрыше у игроков ещё нет никакой информации, поэтому первый игрок выбирает стратегию произвольно. Далее каждый игрок выбирает такую чистую стратегию, которая является наилучшей с учетом всех предыдущих ходов противника, рассматриваемых как некоторая «смешанная» стратегия, т.е. последовательно, при каждом розыгрыше выбирается та стратегия, которая первому игроку дает максимальный средний выигрыш, а второму - минимальный средний проигрыш. После каждого розыгрыша вычисляется среднее значение выигрыша первого игрока, проигрыша второго игрока, и их среднее арифметическое принимается за приближенное значение цены игры. После завершения итерационного процесса вычисляются частоты использования игроками своих стратегий, которые являются приближенными значениями вероятностей в оптимальных смешанных стратегиях игроков[1].
Обозначения:
N - номер розыгрыша (итерации);
i(N) – номер чистой стратегии 1-го игрока, выбранной в партии N;
Lj(N) – общий выигрыш 1-го игрока после N партий, если 2-й игрок все время применяет стратегию yj;
v1^(N) =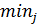 
(Lj(N))/N – наименьший средний выигрыш 1-го игрока за N ходов;
j(N) – номер чистой стратегии 2-го игрока в партии N;
Ui(N) – общий выигрыш 1-го игрока после N партий, если он все время использует стратегию xi;
v2^(N) =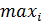 
(Ui(N))/N – наибольший средний выигрыш 1-го игрока за N ходов;
ν = (ν1+ ν2)/2 - приближенное значение цены игры.
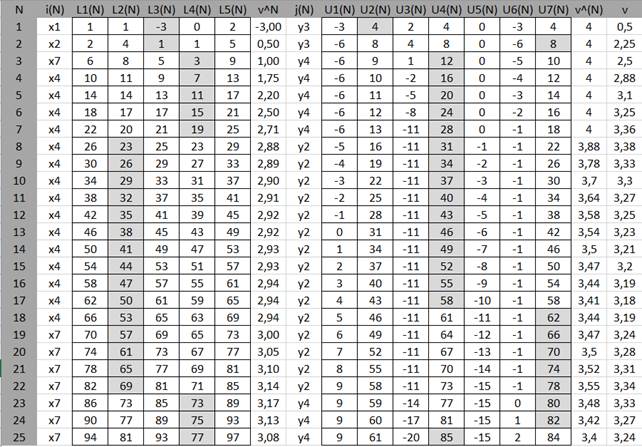
Таблица 3. Итерационный процесс.
Выполнив 25 итераций, можно найти приближённое решение игры: цена игры приравнивается к цене игры последней итерации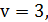 
24; вероятности использования первым и вторым игроками определённых стратегий соответственно равны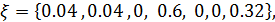 
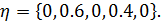
Определим, являются ли оптимальными полученные в приближенном решении стратегии игроков. Для этого определим величину среднего выигрыша:
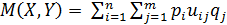= 3.29
Проверим, выполняется ли для всех строк соотношение
.
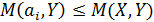При проверке стратегии a4 не выполняется данное условие:
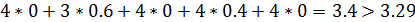
Таким образом, данный план не оптимален.
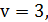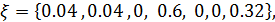
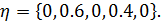Ответ: 24; План не оптимален.
б) найти решение игры точным методом – путём сведения игровой задачи к паре двойственных задач линейного программирования (для решения составить программу):
Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок (если только тот не выходит за пределы своих активных стратегий), оптимальная стратегия 1-го игрока X* гарантирует ему выигрыш не меньше ν*, независимо от стратегии, выбранной 2-м игроком[2], поэтому:
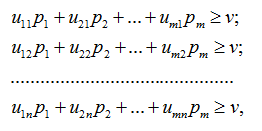
Где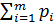 
=1,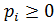 
;
Сделаем подстановку:
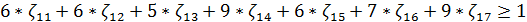
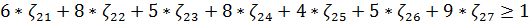
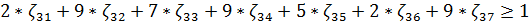
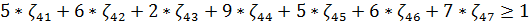
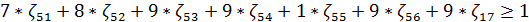
Поскольку игрок I стремится максимизировать цену игры ν, то
величина обратная 1/ν будет минимизироваться.
Решим симплекс методом, выполним подстановку и получим ответ для первого игрока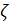 
(0,0,0,2/3,0,0,1/3).
Аналогичным образом выглядит прямая задача ЛП для второго игрока:
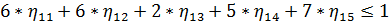
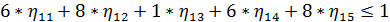
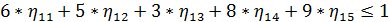
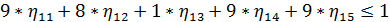
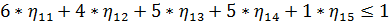
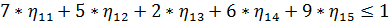
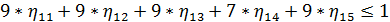
Сама функция максимизируется:
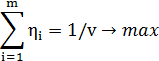
Решим симплекс методом, выполним подстановку и получим ответ для второго игрока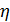 
(0,2/3,0,1/3,0)
Таким образом, с помощью симплекс метода можно получить точное решение задачи.
Ответ: 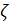(0,0,0,2/3,0,0,1/3), 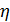(0,2/3,0,1/3,0), V=3.33.
1.2 Листинг программного кода для решения игры путём сведения игровой задачи к паре двойственных задач линейного программирования:
Решение системы на максимизацию функции
class Simplex
{
public:
Simplex(vector<vector<double> > & source)
{
m = source.size();
n = source[0].size();
table.resize(m, vector<double>(n + m - 1));
for (int i = 0; i < m; i++)
{
for (int j = 0; j < table[i].size(); j++)
{
if (j < n)
table[i][j] = source[i][j];
else
table[i][j] = 0;
}
//выставляем коэффициент 1 перед базисной переменной в строке
if ((n + i) < table[i].size())
{
table[i][n + i] = 1;
basis.push_back(n + i);
}
}
coef = table[table.size() - 1];
for (int i = 0; i < coef.size(); ++i)
coef[i] = fabs(coef[i]);
n = table[0].size();
}
//result - в этот массив будут записаны полученные значения X
vector<vector<double> > Calculate(vector<double> & result)
{
int mainCol, mainRow; //ведущие столбец и строка
while (!IsItEnd())
{
mainCol = findMainCol();
mainRow = findMainRow(mainCol);
basis[mainRow] = mainCol;
vector<vector<double> > new_table(m, vector<double>(n));
for (int j = 0; j < n; j++)
new_table[mainRow][j] = table[mainRow][j] / table[mainRow][mainCol];
for (int i = 0; i < m; i++)
{
if (i == mainRow)
continue;
for (int j = 0; j < n; j++)
new_table[i][j] = table[i][j] - table[i][mainCol] * new_table[mainRow][j];
}
table = new_table;
}
//заносим в result найденные значения X
for (int i = 0; i < result.size(); i++)
{
int k = IndexOf(basis, i + 1);
if (k!= -1)
result[i] = table[k][0];
else
result[i] = 0;
}
return table;
}
double Len(const vector<double> & result)
{
double F = 0;
for (int i = 0; i < result.size(); i++)
{
F += coef[i] * result[i];
}
return F;
}
private:
int IndexOf(const vector<int> & basis, int value)
{
for (int i = 0; i < basis.size(); ++i)
{
if (basis[i] == value) return i;
}
return -1;
}
bool IsItEnd()
{
bool flag = true;
for (int j = 1; j < n; j++)
{
if (table[m - 1][j] < 0)
{
flag = false;
break;
}
}
return flag;
}
int findMainCol()
{
int mainCol = 1;
for (int j = 2; j < n; j++)
if (table[m - 1][j] < table[m - 1][mainCol])
mainCol = j;
return mainCol;
}
int findMainRow(int mainCol)
{
int mainRow = 0;
for (int i = 0; i < m - 1; i++)
if (table[i][mainCol] > 0)
{
mainRow = i;
break;
}
for (int i = mainRow + 1; i < m - 1; i++)
if ((table[i][mainCol] > 0) && ((table[i][0] / table[i][mainCol]) <= (table[mainRow][0] / table[mainRow][mainCol])))
mainRow = i;
return mainRow;
}
//source - симплекс таблица без базисных переменных
vector<vector<double> > table; //симплекс таблица
int m, n;
vector<double> coef;
vector<int> basis; //список базисных переменных
};
Решение системы на минимум
class SimplexMin
{
public:
SimplexMin(vector<vector<double> > & source)
{
m = source.size();
n = source[0].size();
table.resize(m, vector<double>(n + m - 1));
for (int i = 0; i < m; i++)
{
for (int j = 0; j < table[i].size(); j++)
{
if (j < n)
table[i][j] = source[i][j];
else
table[i][j] = 0;
}
//выставляем коэффициент 1 перед базисной переменной в строке
if ((n + i) < table[i].size())
{
table[i][n + i] = 1;
basis.push_back(n + i);
}
}
for (int j = 1; j < n; ++j)
{
coef.push_back(table[table.size() - 1][j]);
}
n = table[0].size();
}
//result - в этот массив будут записаны полученные значения X
vector<vector<double> > Calculate(vector<double> & result)
{
int mainCol, mainRow; //ведущие столбец и строка
while (!IsItEnd())
{
mainRow = findMainRow();
mainCol = findMainCol(mainRow);
basis[mainRow] = mainCol;
vector<vector<double> > new_table(m, vector<double>(n));
for (int j = 0; j < n; j++)
new_table[mainRow][j] = table[mainRow][j] / table[mainRow][mainCol];
for (int i = 0; i < m; i++)
{
if (i == mainRow)
continue;
for (int j = 0; j < n; j++)
new_table[i][j] = table[i][j] - table[i][mainCol] * new_table[mainRow][j];
}
table = new_table;
}
//заносим в result найденные значения X
for (int i = 0; i < result.size(); i++)
{
int k = IndexOf(basis, i + 1);
if (k!= -1)
result[i] = table[k][0];
else
result[i] = 0;
}
return table;
}
double Len(const vector<double> & result)
{
double F = 0;
for (int i = 0; i < result.size(); i++)
{
F += coef[i] * result[i];
}
return F;
}
private:
int IndexOf(const vector<int> & basis, int value)
{
for (int i = 0; i < basis.size(); ++i)
{
if (basis[i] == value) return i;
}
return -1;
}
bool IsItEnd()
{
bool flag = true;
for (int i = 0; i < m - 1; i++)
{
if (table[i][0] < 0)
{
flag = false;
break;
}
}
return flag;
}
int findMainCol(int mainRow)
{
int mainCol = 1;
double mmin = 1e9;
for (int j = 1; j < table[0].size(); j++)
if (table[mainRow][j] < mmin)
mainCol = j, mmin = table[mainRow][j];
return mainCol;
}
int findMainRow()
{
int mainRow = 0;
for (int i = 0; i < table.size() - 1; ++i)
if (table[i][0]!= 0) mainRow = i;
double mmin = 1e9;
for (int i = 0; i < table.size() - 1; ++i)
{
if (table[i][0] <= mmin && table[i][0]!= 0)
mainRow = i, mmin = table[i][0];
}
return mainRow;
}
//source - симплекс таблица без базисных переменных
vector<vector<double> > table; //симплекс таблица
int m, n;
vector<double> coef;
vector<int> basis; //список базисных переменных
};
Класс взаимодействия с пользователем
class MainIntecator
{
public:
MainIntecator(){}
void InputTable()
{
cout << "input n, m" << endl;
cin >> _n >> _m;
table.resize(_n, vector<double>(_m));
_delta = 0;
for (int i = 0; i < _n; ++i)
for (int j = 0; j < _m; ++j)
{
cin >> table[i][j];
_delta = min(_delta, table[i][j]);
}
MakeItPositive();
}
void Run()
{
if (UpperAndLowerBounds()) cout << _upperLowerBounds.first << endl;
else
{
SetTableMax();
SetTableMin();
vector<double> resultMin(_n), resultMax(_m);
Simplex Smax(tableMax);
Smax.Calculate(resultMax);
SimplexMin Smin(tableMin);
Smin.Calculate(resultMin);
double v = 0;
for (int i = 0; i < resultMax.size(); ++i)
v += resultMax[i];
v = 1 / v;
cout << "prise = " << v - _delta << endl;
for (int i = 0; i < resultMin.size(); ++i)
{
cout << "ei = " << resultMin[i] << " ";
}
cout << endl;
for (int i = 0; i < resultMax.size(); ++i)
{
cout << "ni = " << resultMax[i]<< " ";
}
cout << endl;
}
}
private:
void SetTableMin()
{
tableMin.resize(tableMax[0].size(), vector<double>(tableMax.size(), -1));
for (int i = 1; i < tableMin[0].size(); ++i)// заполнили последнюю строку
tableMin[_m][i] = 1;
for (int i = 0; i < _m; ++i)
{
tableMin[i][0] = -1;
for (int j = 1; j <= _n; ++j)
{
tableMin[i][j] = table[j - 1][i] * -1;
}
}
}
void SetTableMax()
{
tableMax.resize(_n + 1);
for (int i = 0; i < _n; ++i)
{
tableMax[i].push_back(1);
for (int j = 0; j < table[i].size(); ++j)
tableMax[i].push_back(table[i][j]);
}
tableMax[_n].push_back(0);
for (int i = 0; i < table[0].size(); ++i)
tableMax[_n].push_back(-1);
}
bool UpperAndLowerBounds()// true если верхняя и нижняя цены игры равны, то есть если есть седло
{
vector<int> mmin, mmax;
for (int i = 0; i < _n; ++i)
mmin.push_back(*min_element(table[i].begin(), table[i].end()));
_upperLowerBounds.first = *max_element(mmin.begin(), mmin.end());
for (int j = 0; j < _m; ++j)
{
double localMax = -1e9;
for (int i = 0; i < _n; ++i)
{
localMax = max(localMax, table[i][j]);
}
mmax.push_back(localMax);
}
_upperLowerBounds.second = *min_element(mmax.begin(), mmax.end());
return _upperLowerBounds.first == _upperLowerBounds.second;
}
void MakeItPositive()
{
if (_delta == 0) return;
_delta = -1 * _delta + 1;
for (int i = 0; i < _n; ++i)
for (int j = 0; j < _m; ++j)
table[i][j] += _delta;
}
vector<vector<double> > table; // исходная таблица игры
vector<vector<double> > tableMin;// матрица для симплекса первого игрока
vector<vector<double> > tableMax;// матрица симплекса второго(прямая матрица с поменянным первым столбцом и отрицаетльным Z
double _delta; // сдвиг для преобразования матрицы в положительную
int _n, _m;
pair<double, double> _upperLowerBounds;
};
г) попробовать упростить задачу путём исключения доминируемых стратегий обоих игроков. Если хотя бы у одного из игроков останется 2 активных стратегии, то решить задачу графическим методом:
Проверим матрицу выигрыша (Таблица 1) на дублирующийся стратегии: таких нет.
Проверим на доминируемые и доминирующие стратегии:
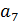доминирует над 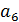, удалим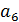
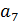доминирует над 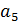, удалим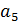
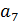доминирует над 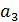, удалим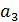
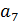доминирует над , удалим
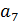доминирует над 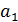, удалим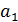
Теперь матрица примет вид (таблица 4).
|
|
|
|
|
| |
|
| |||||
|
|
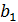
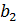
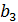
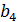
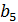
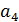
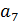
Таблица 4. Матрица выигрыша, упрощённая по строкам.
Проверим теперь столбцы:
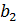доминирует над 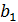, удалим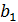
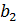доминирует над 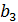, удалим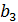
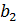доминирует над 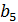, удалим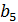
Теперь матрица примет вид (таблица 5).
|
|
| |
|
| ||
|
|
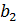
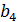
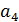
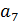
Таблица 5. Матрица выигрыша, упрощённая по строкам и столбцам.
Для игры с матрицей выигрыша 2*2 можно получить решение графическим методом.
Для первого игрока решение будет иметь вид (Рисунок 1) 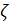(0,0,0,2/3,0,0,1/3).
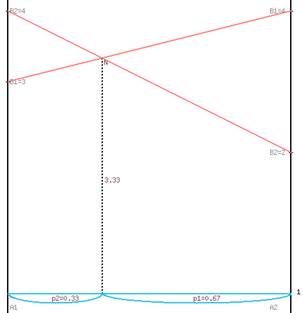
Рисунок 1. Графическое представление решения для первого игрока.
Для второго игрока решение будет иметь вид (Рисунок 2) 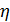(0,2/3,0,1/3,0).
Рисунок 2. Графическое представление решения для второго игрока.
Так как получилась матрица 2*2, воспользуемся формулами для проверки.
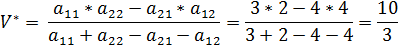
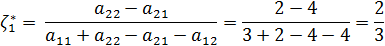
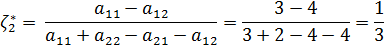
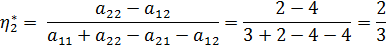
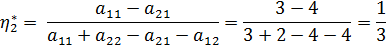
Таким образом, полученное в графическом методе решение с достаточной долей достоверности соответствует точному решению, полученному с помощью формул.
Ответ: 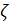(0,0,0,2/3,0,0,1/3), 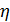(0,2/3,0,1/3,0), V=3.33;