Постановка задачи:
Планируется выпуск новой продукции, для чего необходимо закупить технологическое оборудование. Система оптовой торговли может поставить не более N комплектов технологического оборудования. При этом каждая партия поставки составляет 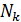 штук, а минимальный объем поставок
штук, а минимальный объем поставок  штук. Соответственно, вектор решений об объёме поставок
штук. Соответственно, вектор решений об объёме поставок
 (1)
(1)
Ежегодный доход от продукции, снимаемой с одного технологического оборудования, составляет A тыс. руб. Оптовая цена одной единицы технологического оборудования B тыс. руб., эксплуатационные расходы R тыс. руб., затраты на подготовку производства P тыс. руб., причём они не зависят от числа единиц технологического оборудования и объема выпуска. Пусть спрос пропорционален количеству продукции, снимаемой с m работающих единиц технологического оборудования, и для простоты ограничимся вектором состояний спроса
 (2)
(2)
– как вектором возможных условий среды. Если решающее правило сформулировать как «доход минус издержки», то планово- экономический отдел предприятия предлагает рассчитывать элементы матрицы решений (как матрицы выигрышей) по формуле:
 (3)
(3)
Исходные параметры задачи: N=70; 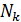 =10;
=10;  = 20; A=437; B=52; R=13; P=110.
= 20; A=437; B=52; R=13; P=110.
Распределение вероятностей условий среды:  =0,05;
=0,05;  =0,1;
=0,1;  =0,15;
=0,15;  =0,2;
=0,2; 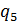 =0,3;
=0,3;  =0,05;
=0,05;  =0,15.
=0,15.
Необходимо к построенной выше матрице решений применить классические (MM-,BL-, S-) и производные (HW-, HL, G-, P-) критерии принятия решения.
При этом:
- при принятии решения с помощью HW- и HL-критериев первоначально положить параметры c = v = 0,5. Определить для этих критериев значения параметров (с точностью до второго знака после запятой), при которых найденное оптимальное решение изменяется;
- сравнить результаты.
Построить сводную таблицу критериев, в которой отразить использованные критерии и оптимальные для них альтернативы с условиями, при которых они оптимальны. Привести сравнение полученных оптимальных альтернатив при разных критериях. Сделать вывод – рекомендуемые в итоге оптимальные альтернативы с их обоснованием – сравнить значения критериев.
Решение:
Матрица, описывающая поведение игрока и природы представлена в таблице 6.
| -1150 | ||||||
| -1670 | ||||||
| -2190 | ||||||
| -2710 | ||||||
| -3230 | ||||||
| -3750 |
Таблица 6. Матрица выигрыша первого игрока в игре с природой.
| Критерий | Оптимальные альтернативы | Условия оптимальности |
| ММ | 
| о возможности появления внешних состояний Fj ничего не известно; приходится считаться с появлением различных внешних состояний Fj; решение реализуется однократно или небольшое число раз; необходимо исключить какой бы то ни было риск. |
| Сэвиджа(S) | 
| Аналогично ММ |
| Произведений(P) | 
| вероятности появления состояний Fj неизвестны; с появлением всех состояний необходимо считаться; допускается некоторый риск; критерий применим и при малом числе реализаций. |
| Байеса-Лапласса(BL) | 
| вероятности появления состояний Fj известны и не зависят от времени; решение реализуется многократно; для малого числа реализаций решения допускается некоторый риск. |
| Ходжа-Лемана (HL) | 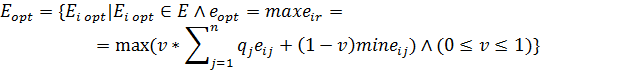
| точные вероятности появления состояний Fj неизвестны, но некоторые предположения о распределениях вероятностей возможны; принятое решение теоретически допускает бесконечно много реализаций; при малых числах реализаций допускается некоторый риск. |
| Гермейера(G) | 
| вероятности появления состояний Fj известны; с появлением тех или иных состояний необходимо считаться; допускается некоторый риск; решение может реализоваться один или много раз. |
| Критерий Гурвица (HW) | 
| о вероятностях появления состояний Fj ничего не известно; с появлением состояний Fj необходимо считаться; ситуация принятия решения реализуется малое число раз; допускается некоторый риск (при уменьшении значения c). |
Таблица 7. Сводная таблица критериев.
| MM | BL | S | HW | HL | G | P | |
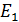
| + | 0.378 | |||||

| |||||||
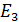
| |||||||

| V = 0.168 | 0.5 | + | + | |||

| |||||||

| + | + | V=0.5 |
Таблица 8. Сводная таблица применения критериев принятия решения к задаче.
Вывод: следует предпочесть вариант Е4, поскольку большинство критериев отдает предпочтение именно этому варианту. Метод Ходжа-Лемана ( HL) с нейтральной степенью доверия, так же указывает на 4 стратегию, это значит, что данный метод показал, на мой взгляд, рациональное решение, находящееся между полным пессимизмом и методом Байеса-Лапласса (BL), допускающему некоторый риск при однократном использовании. Метод Гурвица (HW) с множителем 0,168 показывает стратегию с риском, то есть частично азартного игрока. Критерии Гермейера (G) и произведений (P) так же применимы для малого числа реализаций и в данных критериях не известны вероятности состояний природы.
Часть вторая
Во второй части будет рассмотрен метод анализа иерархии и свертки критериев. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Свертка критериев применяется, когда необходимо принять единственное возможное решение.
Постановка задачи:
Руководство вуза в качестве эксперимента организовало конкурс среди преподавателей вуза на право проведения занятий по дисциплине «Проектирование информационных систем». В конкурсную комиссию поступило 7 заявок – В1-В7. Необходимо из них выбрать наилучшую. При этом каждая заявка имеет оценки по шести критериям (Таблица 9): К1 – качество имеющихся учебно-методических разработок преподавателя (оценивается от 0 до 10 баллов); К2 – количество авторских учебно-методических разработок по данной или аналогичной дисциплине за последние 5лет; К3 –срок последнего повышения квалификации по дисциплине (лет назад – чем меньше, тем лучше); К4 – количество студентов, которым преподавалась данная или аналогичная дисциплина за последние 5лет; К5 – научные показатели преподавателя (оценивается от 0 до 10 баллов); К6 – опыт практической деятельности преподавателя, связанный с преподаваемой или аналогичной дисциплиной (оценивается от 0 до 100 баллов).
| K1 | K2 | K3 | K4 | K5 | K6 | |
| B1 | 7.5 | |||||
| B2 | 7.5 | |||||
| B3 | ||||||
| B4 | 5.6 | |||||
| B5 | ||||||
| B6 | 9.1 | |||||
| B7 | 8.3 |
Таблица 9. Оценки участников по критериям.
1 Построить иерархию задачи и решить ее с помощью метода анализа иерархии (МАИ). Все матрицы парных сравнений должны быть согласованными – с ОС < 0,2. Вычисление собственного вектора матриц выполнить по формуле среднего геометрического.
2 Осуществить выявление наилучшей альтернативы, используя свёртки: мультипликативная (вес в показателе степени), агрегирования (cp=10), свертка на основе идеальной точки с метрикой Хемминга, Гермейера. Вычисления выполнить в Excel. Здесь и далее при необходимости использовать веса.
3 Сравнить полученные в п. 1, 2 наилучшие альтернативы, сделать выводы. Сформулировать рекомендации для ЛПР по принятию итогового решения.
Решение:
1. Составим иерархию.

Рисунок 3. Иерархия задачи.
Пусть предпочтения ЛПР выражены в следующем упорядочении критериев:

Построим матрицу парных сравнений критериев (таблица 10).
Вычислим для каждой матрицы индекс согласованности.
| К1 | К2 | К3 | К4 | К5 | К6 | вектор приоритетов | |
| К1 | 0,33 | 0,50 | 3,00 | 0,20 | 0,20 | 0,063542478 | |
| К2 | 2,00 | 4,00 | 0,33 | 0,50 | 0,153662943 | ||
| К3 | 0,5 | 4,00 | 0,25 | 0,25 | 0,096801588 | ||
| К4 | 0,33 | 0,25 | 0,25 | 0,14 | 0,14 | 0,033444106 | |
| К5 | 2,00 | 0,374632712 | |||||
| К6 | 0,5 | 0,277916173 |
Таблица 10. Матрица парных сравнений критериев.
Вычисление индексов согласованности (ИС) и отношений согласованности (ОС) ИС вычисляется следующим образом:
а) суммируются элементы каждого столбца соответствующей матрицы парных сравнений размером n*n;
б) сумма j -гo столбца умножается на j -й элемент нормализованного вектора локальных приоритетов этой матрицы;
в) все полученные таким образом n чисел суммируются, и эта сумма равна 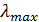 ;
;
г) окончательно получаем:
ИС = 

Рисунок 4. Экспериментально полученные значения случайной согласованности.
Таким образом ОС = 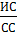

| 6,179673 |
| ис | 0,035935 |
| ос | 0,02898 |
Таблица 11. Значения для матрицы парных сравнений критериев.
Построим матрицы парных сравнений альтернатив по каждому из критериев:
Для каждой заполненной матрицы парных сравнений формируется вектор локальных приоритетов, выражающий относительную важность («ценность») каждого отдельного элемента этой матрицы (критерия или альтернативы) относительно других элементов.
| K1 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | вектор приоритетов |
| B1 | 0,25 | 1,00 | 0,33 | 3,00 | 0,17 | 0,17 | 0,042662144 | |
| B2 | 0,17 | 4,00 | 8,00 | 1,00 | 1,00 | 0,162659541 | ||
| B3 | 0,33 | 3,00 | 0,17 | 0,17 | 0,072456588 | |||
| B4 | 0,25 | 5,00 | 0,25 | 0,25 | 0,092103298 | |||
| B5 | 0,333333 | 0,125 | 0,333333 | 0,2 | 0,13 | 0,13 | 0,018310042 | |
| B6 | 0,316236385 | |||||||
| B7 | 0,295572002 |
Таблица 12. Матрица парных сравнений альтернатив по критерию К1.

| 7,803918 |
| ис | 0,133986 |
| ос | 0,101505 |
Таблица 13. Значения для матрицы парных сравнений по критерию К1.
| K2 | вектор приоритетов | |||||||
| 0,17 | 1,00 | 0,33 | 0,17 | 0,50 | 0,14 | 0,027377291 | ||
| 6,00 | 3,00 | 1,00 | 5,00 | 0,50 | 0,235799603 | |||
| 0,166667 | 0,33 | 0,17 | 0,50 | 0,14 | 0,027377291 | |||
| 0,333333 | 0,33 | 2,00 | 0,25 | 0,082631209 | ||||
| 5,00 | 0,50 | 0,235799603 | ||||||
| 0,2 | 0,5 | 0,2 | 0,17 | 0,045165369 | ||||
| 0,345849633 |
Таблица 14. Матрица парных сравнений альтернатив по критерию К2.

| 6,479875 |
| ис | 0,086688 |
| ос | 0,065672 |
Таблица 15. Значения для матрицы парных сравнений по критерию К2.
| K3 | вектор приоритетов | |||||||
| 0,13 | 0,50 | 0,50 | 0,13 | 0,25 | 0,25 | 0,024743824 | ||
| 6,00 | 6,00 | 1,00 | 4,00 | 4,00 | 0,40374971 | |||
| 0,166667 | 1,00 | 0,17 | 0,50 | 0,50 | 0,048525654 | |||
| 0,166667 | 0,17 | 0,50 | 0,50 | 0,048525654 | ||||
| 0,25 | 0,25 | 0,160228179 | ||||||
| 0,25 | 1,00 | 0,15711349 | ||||||
| 0,25 | 0,15711349 |
Таблица 16. Матрица парных сравнений альтернатив по критерию К3.

| 7,739868 |
| ис | 0,123311 |
| ос | 0,093418 |
Таблица 17. Значения для матрицы парных сравнений по критерию К3.
| K4 | вектор приоритетов | |||||||
| 0,14 | 0,17 | 0,11 | 2,00 | 0,33 | 0,20 | 0,021347551 | ||
| 3,00 | 0,25 | 8,00 | 4,00 | 5,00 | 0,246691079 | |||
| 0,333333 | 0,17 | 6,00 | 0,50 | 0,33 | 0,066873392 | |||
| 9,00 | 6,00 | 5,00 | 0,500122603 | |||||
| 0,5 | 0,125 | 0,166667 | 0,111111 | 0,17 | 0,13 | 0,013650474 | ||
| 0,25 | 0,166667 | 0,33 | 0,071548725 | |||||
| 0,2 | 0,2 | 0,2 | 0,079766175 |
Таблица 18. Матрица парных сравнений альтернатив по критерию К4.

| 6,582172 |
| ис | 0,069638 |
| ос | 0,052756 |
Таблица 19. Значения для матрицы парных сравнений по критерию К4.
| K5 | вектор приоритетов | |||||||
| 1,00 | 0,33 | 3,00 | 0,50 | 0,33 | 0,50 | 0,070167091 | ||
| 0,33 | 3,00 | 0,50 | 0,33 | 0,50 | 0,070167091 | |||
| 4,00 | 3,00 | 0,50 | 2,00 | 0,231686631 | ||||
| 0,333333 | 0,333333 | 0,25 | 0,33 | 0,20 | 0,25 | 0,029529407 | ||
| 0,333333 | 0,50 | 0,50 | 0,106168826 | |||||
| 0,50 | 0,224752277 | |||||||
| 0,267528677 |
Таблица 20. Матрица парных сравнений альтернатив по критерию К5.

| 7,810608 |
| ис | 0,135101 |
| ос | 0,10235 |
Таблица21. Значения для матрицы парных сравнений по критерию К5.
| K6 | вектор приоритетов | |||||||
| 0,33 | 0,50 | 2,00 | 0,25 | 0,33 | 0,25 | 0,047846172 | ||
| 2,00 | 4,00 | 0,50 | 2,00 | 1,00 | 0,186041352 | |||
| 0,5 | 0,33 | 0,33 | 1,00 | 0,50 | 0,067664706 | |||
| 0,5 | 0,25 | 0,20 | 0,33 | 0,25 | 0,047013323 | |||
| 3,00 | 2,00 | 0,327941489 | ||||||
| 0,5 | 0,333333 | 0,50 | 0,104412179 | |||||
| 0,5 | 0,219080779 |
Таблица 22. Матрица парных сравнений альтернатив по критерию К6.

| 7,002448 |
| ис | 0,000408 |
| ос | 0,000309 |
Таблица 23. Значения для матрицы парных сравнений по критерию К6.
Все матрицы парных сравнений являются согласованными ос <0,2.
Для того чтобы получить результирующий набор, перемножим вектор-столбец локальных приоритетов с матрицей попарных сравнений критериев:
| 0,063542478 | 0,042662144 | 0,027377 | 0,024744 | 0,021348 | 0,070167 | 0,047846 | 0,049611037 | ||
| 0,153662943 | 0,162659541 | 0,2358 | 0,40375 | 0,246691 | 0,070167 | 0,186041 | 0,171894215 | ||
| 0,096801588 | * | 0,072456588 | 0,027377 | 0,048526 | 0,066873 | 0,231687 | 0,067665 | = | 0,121347334 |
| 0,033444106 | 0,092103298 | 0,082631 | 0,048526 | 0,500123 | 0,029529 | 0,047013 | 0,064101785 | ||
| 0,374632712 | 0,018310042 | 0,2358 | 0,160228 | 0,01365 | 0,106169 | 0,327941 | 0,184278555 | ||
| 0,277916173 | 0,316236385 | 0,045165 | 0,157113 | 0,071549 | 0,224752 | 0,104412 | 0,157853794 | ||
| 0,295572002 | 0,34585 | 0,157113 | 0,079766 | 0,267529 | 0,219081 | 0,250913279 |
Таблица 24. Получение вектора глобальных приоритетов.
Ответ: 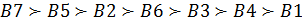
2. Решение задачи с помощью свёрток (Таблица 25):
| Название свертки | Особенности расчета |
| мультипликативная | 
|
| агрегирования (cp=10) | 
|
| свертка на основе идеальной точки с метрикой Хемминга | 
|
| Гермейера | 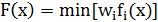
|
Таблица 25. Используемые свертки.
Так как исходная таблица не нормирована, нормируем ее по формуле

Так как критерий – срок последнего повышения квалификации по дисциплине (лет назад – чем меньше, тем лучше), необходимо минимизировать, приведем его к задаче максимизации.
Тогда матрица примет вид (таблица 26).
| k1 | k2 | k3 | k4 | k5 | k6 | max | |
| b1 | 0,285714 | 0,129973 | 0,542857 | 0,255319 | 0,542857 | ||
| b2 | 0,857143 | 0,649867 | 0,542857 | 0,787234 | |||
| b3 | 0,285714 | 0,25 | 0,35809 | 0,971429 | 0,617021 | 0,971429 | |
| b4 | 0,571429 | 0,428571 | 0,25 | ||||
| b5 | 0,857143 | 0,685714 | |||||
| b6 | 0,142857 | 0,5 | 0,506631 | 0,617021 | |||
| b7 | 0,5 | 0,32626 | 0,771429 | 0,808511 |
Таблица 26. Нормированная матрица.
Выполним мультипликативную свертку (Таблица 27). Вообще, для нее не нужна нормализация, но критерии, на мой взгляд, невероятно различны.
Используем веса (важности) критериев, полученные методом МАИ.
| 0,716445 |
| 0,592713 |
| 0,770394 |
Таблица 27. Результат мультипликативной свертки.
Свертка агрегирования или осреднения (Таблица 28).
| 0,203372587 |
| 0,227658452 |
| 0,363948548 |
| 0,065880412 |
| 0,288554979 |
| 0,374647834 |
| 0,2913032 |
Таблица 28. Результат осреднения.
Свертка Гермейера (Таблица 31).
Осуществим нормирование критериев, но приведем все критерии к минимизации (для исходной задачи это означает приведение всех, кроме 3 критерия).
| k1 | k2 | k3 | k4 | k5 | k6 | |
| b1 | -3 | -2 | -128 | -7,5 | -55 | |
| b2 | -8 | -8 | -324 | -7,5 | -80 | |
| b3 | -3 | -2 | -214 | -9 | -72 | |
| b4 | -5 | -5 | -456 | -5,6 | -43 | |
| b5 | -1 | -8 | -79 | -8 | -90 | |
| b6 | -8 | -3 | -270 | -9,1 | -72 | |
| b7 | -8 | -9 | -202 | -8,3 | -81 | |
| max | -1 | -2 | -79 | -5,6 | -43 | |
| min | -8 | -9 | -456 | -9,1 | -90 |
Таблица 29. Таблица, приведённая к минимизации.
| k1 | k2 | k3 | k4 | k5 | k6 | max | |
| b1 | 0,714286 | 0,870027 | 0,457143 | 0,744681 | |||
| b2 | 0,142857 | 0,350133 | 0,457143 | 0,212766 | 0,457143 | ||
| b3 | 0,714286 | 0,75 | 0,64191 | 0,028571 | 0,382979 | ||
| b4 | 0,428571 | 0,571429 | 0,75 | ||||
| b5 | 0,142857 | 0,314286 | |||||
| b6 | 0,857143 | 0,5 | 0,493369 | 0,382979 | 0,857143 | ||
| b7 | 0,5 | 0,67374 | 0,228571 | 0,191489 | 0,67374 |
Таблица 30. Нормированная таблица.
| 0,029097 | 1,220243 |
| 0,010704 | 0,076265 |
Таблица 31. Результат свертки Гермейера.
Свертка на основе идеальной точки.
Осуществим нормирование критериев, но с учетом их исходного направления оптимизации. Идеальной точкой будет вектор (1, 1, 0, 1, 1, 1)
Нормированная таблица примет вид (таблица 32)
| k1 | k2 | k3 | k4 | k5 | k6 | max | |
| b1 | 0,285714 | 0,129973 | 0,542857 | 0,255319 | |||
| b2 | 0,857143 | 0,649867 | 0,542857 | 0,787234 | |||
| b3 | 0,285714 | 0,75 | 0,35809 | 0,971429 | 0,617021 | 0,971429 | |
| b4 | 0,571429 | 0,428571 | 0,75 | ||||
| b5 | 0,857143 | 0,685714 | |||||
| b6 | 0,142857 | 0,5 | 0,506631 | 0,617021 | |||
| b7 | 0,5 | 0,32626 | 0,771429 | 0,808511 | |||
Таблица 32. Нормированная таблица.
Тогда результат по метрике Хэмминга:
| 0,703169 |
| 0,264053 |
| 0,410259 |
| 0,84019 |
| 0,23668 |
| 0,303048 |
| 0,209782 |
Таблица 33. Результат по метрике Хэмминга.
Сравнение полученных альтернатив представлено в таблице 34.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
| метрика Хэмминга | |||||||
| Гермейер | + | + | + | + | |||
| агрегирования | |||||||
| Мультипликативная | |||||||
| МАИ |
Таблица 34. Сравнение альтернатив с учётом всех используемых метрик.
Вывод: из-за того, что каждая свертка допускает некоторые уступки, будь то сглаживание уровней частных критериев за счет неравнозначных первоначальных значений частных критериев, требуют значительных личных предпочтений экспертов, то для того, чтобы принять решение, можно усреднить результаты, полученные в сводной таблице, если каждому кандидату присвоить баллы, равные сумме его мест в каждом из критериев, то необходимо выбрать кандидата с минимальными баллами. Таковым является кандидат 6.
Часть третья.
В третьей части будет рассматриваться задача группового принятия решения.
Постановка задачи:
1 Найти наилучшую альтернативу (Таблица 35), используя модифицированную процедуру Борда, процедуры Кондорсе, Доджсона, процедуры Кумбса, Фишберна.
2 Сравнить полученные результаты, сделать выводы. Сформулировать рекомендации ГПР по итоговому решению.
| Число голосов | Варианты упорядочивания проектов |
| A®B®C®D | |
| A®B®D®C | |
| A®C®B®D | |
| A®C®D®B | |
| A®D®B®C | |
| B®A®D®C | |
| B®C®D®A | |
| B®D®A®C | |
| B®D®C®A | |
| C®B®A®D | |
| C®D®A®B | |
| D®A®C®B | |
| D®B®A®C | |
| D®C®A®B | |
| D®C®B®A |
Таблица 35. Условия задачи группового принятия решений.
Решение модифицированным методом Борда.
Строим парные сравнения (Таблица 36).
| AB | |
| AC | |
| AD | |
| BA | |
| BC | |
| BD | |
| CA | |
| CB | |
| CD | |
| DA | |
| DB | |
| DC |
Таблица 36. Таблица парных сравнений.
Вычислим функцию Борда:
A = 8
B = -102
C = -40
D = 134
Отсортируем по убыванию, и получим результат:

Процедура Кондорce
Воспользуемся матрицей парных сравнений, полученной в методе Борда (Таблица 36).
Запишем таблицу в удобной для восприятия форме.
Восстановим последовательность:

Процедура Доджсона
Для парных сравнений строим матрицу Джонсона (Таблица 37)
| A | B | C | D | |
| A | 158/142 | 161/139 | 135/165=0.8181 | |
| B | 142/158 = 0.898 | 129/171=0.75 | 128/172=0.726 | |
| C | 139/1610=0.844 | 172/129 | 120/180=0.66 | |
| D | 165/135 | 172/128 | 180/120 |
Таблица 37. Матрица Джонсона.
Вычисляем функции Доджсона для альтернатив A1/2 = 300/2 = 150
в матрице Доджсона нет элементов, принадлежащих множеству A1/2, поэтому кандидат D является безусловным победителем – он при всех попарных сравнениях имеет более голосов.
Предпочтения по остальным кандидатам определяется минимальным значением функции Доджсона

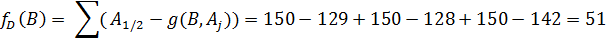

Отсюда имеем итоговое упорядочение

Процедура Кумбса.
Посчитаем для каждой итерации худших кандидатов:
| Номер итерации | Результаты | Исключенный кандидат |
| A 62 B 94 C 97 D 47 | C | |
| A 108 B 72 D 82 | A | |
| B 75 D 78 | D | |
| B 59 | B |
Таблица 38. Итерированный процесс исключения кандидатов.
Результирующий набор имеет вид

Процедура Фишберна.
Построим матрицу парных сравнений кандидатов, и определим в скольких случаях каждый из них доминирует (по простому числу голосов) над другими (Таблица 39).
| кандидат | Значение функции Фишберна |
| A | |
| B | |
| C | |
| D |
Таблица 39. Результат применения функции Фишберна.
Отсортируем кандидатов по убыванию значения функции Фишберна.
Тогда заключительный вариант примет вид:

Сравним полученные результаты (Таблица 40).
| метод | результат |
| Процедура Борда | 
|
| Процедура Кондорсе | 
|
| Процедура Доджсона | 
|
| Процедура Кумбса. | 
|
| Процедура Фишберна | 
|
Таблица 40. Сравнение результатов.
По правилу относительного большинства и Борда победителем окажется также D. По правилу Кумбса победитель — B. Как выяснилось в большинстве случаев, разные процедуры голосования дают одинаковый результат, но существуют исключительные случаи: в нашем примере — коллективное решение, полученное процедурой Кумбса.
ЗАКЛЮЧЕНИЕ
В результате проделанной работы были закреплены знания по задачам принятия решений методами теории игр, методами статистических решений. Освоены методы анализа иерархии и свертки критериев, получен опыт решения задач группового принятия решений.
В первой части решена задача принятия решения методами теории игр и методами статистических решений, которые разработаны для поиска оптимальной стратегии или стратегий в игре двух лиц. Безусловно, в первую очередь имеет смысл упрощение исходной матрицы выигрыша. В этом случае можно свести задачу к графическому методу, который является одним из самых быстрых и простых. В случае же неудачи следует свести игровую задачу к паре двойственных задач линейного программирования и решать точным методом. Это позволит узнать точный ответ, но займёт много времени. Решение задачи методом последовательных приближений не желательно, так как требуется немалое количество итераций, чтобы приблизиться к точному ответу. В методе статистических решений вторым лицом выступает природа, она не действует злонамерено, поэтому точно определить решение невозможно, но можно выбрать альтернативу, подходящую под определенные условия. Необходимо внимательно изучить все возможные альтернативы и варианты и с полной ответственностью принять решение.
Во второй части был реализован метод анализа иерархии и свертки критериев. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Свертка критериев применяется, когда необходимо принять единственное возможное решение. Несмотря на возможность сверки, необходимо ответственно выбирать метод, который наилучшим образом подходит к цели задачи.
В третьей части разобрана задача группового принятия решения. Стоит отметить, что не является лишним решение задачи комплексом методов, так как в методах наблюдаются расхождения и разумнее делать выводы по большинству похожих результатов.
Программная реализация выполнена на языке высокого уровня С++ в среде разработки Microsoft Visual Studio 2015. Состоит из трех классов, два из которых реализуют прямой и обратный симплекс метод и еще один класс - взаимодействие с пользователем, и подготовка входных матриц к симплекс методу, а именно, произвести прибавление к каждому элементу матрицы положительно числа таким образом, чтобы элементы матрицы стали неотрицательными. Благодаря теореме, которая гласит, что каждая сведенная игровая задача имеет решение, можно не искать зацикливание.
При любом принятии решения следует помнить, что компромисс между мнениями экспертов, методами и здравым смыслом является залогом успешного решения проблемы.