Термодинамические основы гомогенного зародышеобразования (по Гиббсу – Фольмеру)
Возникновение дисперсной системы в результате образования (и последующего роста) зародышевых частиц новой стабильной фазы возможно в любой метастабильной системе. Метастабильность, связанная с удалением от состояния устойчивого равновесия системы, может быть вызвана как отклонением в химическом составе фаз, так и вследствие физико-химических воздействий на систему.
При образовании частицы (зародыша) радиусом r возникает поверхность раздела старой и новой фаз, равная 4πr2, с которой связана поверхностная энергия 4πr2σ. Образование частицы связано с переходом вещества в более стабильное состояние, что сопровождается снижением его химического потенциала от значения μст в старой фазе до более низкого значения μн в новой фазе.
Работа образования зародыша новой фазы W может быть записана в виде:
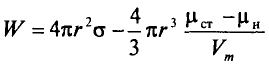

Размер частицы rc равен:
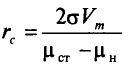
Частица радиусом rc, соответствующему максимуму кривой W(r), называется критическим зародышем новой фазы. Она находится в неустойчивом равновесии со старой фазой.
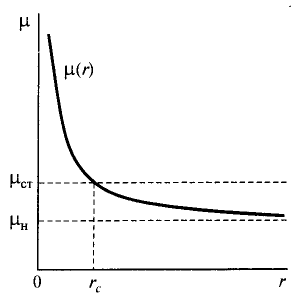
Рисунок 1 – Условия равновесия критического зародыша и старой фазы
Подставим уравнение (2) в уравнение (1) и получим:
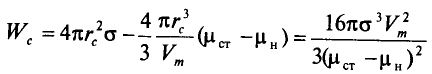
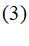
Гетерогенное образование новой фазы
Гомогенное зародышеобразование наблюдается только тогда, когда в системе нет поверхностей, на которых может с достаточной скоростью происходить образование и рост зародышей новой фазы. Если же такие поверхности имеются (например, стенки сосуда и особенно поверхности посторонних включений), то в зависимости от их природы может стать значительно более вероятным гетерогенное образование зародышей новой фазы на этих поверхностях. Если в систему введены затравки самого вещества новой фазы (или вещества, близкого ему по строению и свойствам), то выделение новой фазы идет на поверхности этих затравок.
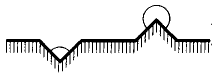
Рисунок 2 – Образование зародышей новой фазы на разных участках шероховатой поверхности
Таким образом, наличие поверхностей, особенно шероховатых, избирательно смачиваемых новой фазой, существенно способствует ее выделению, снижая работу образования критических зародышей, и тем больше, чем лучше смачивание. Поэтому наблюдение чисто гомогенного образования зародышей новой фазы возможно лишь при отсутствии в системе посторонних включений и полном избирательном смачивании стенок сосуда.
Молекулярно-кинетические свойства дисперсных систем
Молекулярно-кинетическая теория изучает законы самопроизвольного движения молекул. Некоторые свойства растворов обусловлены именно этим движением, т. е. определяются не химическим составом, а числом кинетических единиц – молекул в единице объема или массы. К таким коллигативным свойствам относятся: осмотическое давление, диффузия, изменения давления пара и температур замерзания и кипения, поверхностное давление.
Броуновское движение
В 1828 году ботаник Броун при наблюдении в микроскопе взвешенных в воде частиц цветочной пыльцы и спор обнаружил, что они находятся в непрерывном беспорядочном движении, не затухающем во времени. Вначале это явление связывалось с жизненными процессами, но уже сам Броун установил, что оно свойственно любым мельчайшим частицам как органического, так и неорганического происхождения, и проявляется тем интенсивнее, чем выше температура и чем меньше масса частицы и вязкость среды.
Тщательными исследованиями было установлено, что какие бы меры ни принимались для соблюдения точного механического и термического равновесия, движение проявляется всегда одинаковым образом, оно безостановочно, неизменно во времени, вечно. Крупные частицы смещаются незначительно, для более мелких характерно поступательное, беспорядочное по своему направлению движение по весьма сложным траекториям.
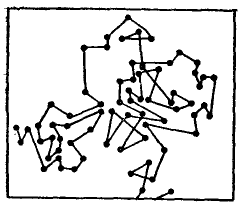
Рисунок 1 – Броуновское движение частицы размером ≈ 1 мкм
Иными словами, движение вызвано столкновениями молекул среды (жидкости или газа) со взвешенными в ней частицами.
Хаотическое движение частицы охватывает определенный объем пространства, возрастающий во времени. В отличие от реального пути частицы, изменяющего направление до 1020 раз в 1 с, усредненная величина Δх2 при совершенной беспорядочности движения может быть точно вычислена на основании статистических законов. Для сферической частицы радиусом r она прямо пропорциональна абсолютной температуре Т и времени наблюдения t и обратно пропорциональна коэффициенту гидродинамического (вязкостного) сопротивления среды ω = 6πηr (где η – коэффициент вязкости):
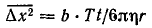
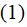
Для коэффициента пропорциональности теория Эйзенштейна дает выражение
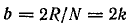
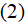
где R – газовая постоянная, N – число Авогадро.
Следовательно:
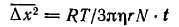
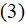
Статистическая теория, приводящая к уравнению (3), получила многочисленные и неоспоримые экспериментальные доказательства.
Осмос
При разделении двух растворов различной концентрации (или раствора и чистого растворителя) полупроницаемой мембраной возникает поток растворителя от меньшей концентрации к большей, выравнивающий концентрации. В дальнейшем поток уравновешивается возникающим встречным градиентом давления. Этот процесс обусловлен, в термодинамической трактовке, ростом энтропии смешения системы, а в кинетической, - избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора.
Для идеальных растворов известно следующее выражение закона Вант-Гоффа
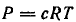
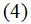
где Р – осмотическое давление; с – молярная концентрация.
Расчет по этому уравнению показывает, что если с = 1М, то Р = 22,4 атм (2,27 МПа).
Концентрации коллоидных растворов обычно очень малы по сравнению с растворами молекулярными.
Практическое отсутствие осмотического давления коллоидных растворов объясняется чрезвычайно малыми значениями частичной концентрации или, иными словами, чрезвычайно большими значениями частичной массы коллоидных частиц по сравнению с молекулярной.
Таким образом, в отношении осмоса не обнаруживается никаких принципиальных качественных различий между коллоидными и молекулярными растворами; основные закономерности едины, но значительные различия концентраций приводят к слабому проявлению осмоса в коллоидных системах.
Диффузия
Диффузией называют процесс самопроизвольного выравнивания концентраций в системе, приводящий к установлению одинакового химического потенциала каждого компонента во всех элементах объема системы.
Для нахождения количественных закономерностей процесса диффузии рассмотрим распределение вещества в пространстве и во времени. Пусть раствор (молекулярный или коллоидный) с концентрацией «с» отделен перегородкой от чистого растворителя (дисперсионной среды). Представим себе далее, что мы вынимаем перегородку без перемешивания в момент времени t = 0 и ведем наблюдение за изменением концентрации в процессе диффузии растворенного вещества слева направо в направлении х. Кривые с = f(x), представленные на рис. 2, показывают распределение вещества в системе в различные моменты времени. Опыт свидетельствует, что эти концентрационные профили 1-5 пересекаются в одной точке и симметричны. Наибольшие изменения концентрации во времени (как это следует из сравнения кривых для различных значений t) происходят там, где наблюдаются наибольшие ее градиенты dc/dx, а именно - вблизи начальной границы раздела АВ.
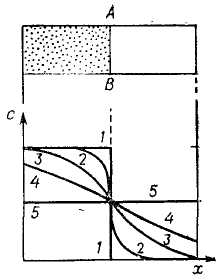
Рисунок 2 – Изменения концентрационных профилей в процессе диффузии за время от t = 0 (1) до t = ∞ (5)
Первый закон Фика
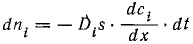
показывает, что количество вещества, переносимое через сечение, нормальное к потоку, пропорционально параметрам s, t и grad c. Физический смысл фактора пропорциональности D, называемого коэффициентом диффузии, определяется формально из уравнения (5), как количество вещества, переносимое через 1 см2 за 1 с при единичном grad c. Величина D является, таким образом, количественной мерой диффузии в стандартных условиях.
Значения D могут быть найдены экспериментально по уравнению (5) путем измерения количества вещества, диффундирующего с известным dc/dx в условиях, исключающих конвекцию. Порядок значений D, найденных из таких опытов для различных систем, составляет 10-5 для обычных молекул и ионов и 10-7 – 10-9 см2/с для коллоидных частиц, т. е. отличается на 2-4 порядка.
Для коллоидных частиц, характеризующихся значением D = 5*10-9 см2/с, время прохождения 1 см составит около трех лет, тогда как для молекул – несколько часов.
Таким образом, для коллоидных систем характерна весьма медленная, но все же измеримая диффузия, позволяющая определить размеры диффундирующих частиц.
Несмотря на все качественное своеобразие, коллоидные системы, в отношении молекулярно-кинетических свойств, принципиально не отличаются от молекулярных растворов. Это не удивительно, так как все особенности коллоидных систем обусловлены изменением доли особенных молекул и всех свойств с ростом дисперсности, а молекулярно-кинетические свойства зависят именно от числа кинетических единиц, которое увеличивается с ростом дисперсности системы.
Таким образом, молекулярно-кинетические свойства коллоидных систем:
- описываются закономерностями, общими для молекулярных и коллоидных растворов;
- выражены значительно слабее, чем в молекулярных растворах, вследствие малых величин частичной концентрации;
- позволяют экспериментально определить важнейшую характеристику коллоидной системы – ее дисперсность (через параметры r, m или Md).