По определению:  , следовательно, существование производной в точке
, следовательно, существование производной в точке  тесно связано с существованием предела
тесно связано с существованием предела  в данной точке.
в данной точке.
В определении производной ВАЖНЕЙШИМ является тот факт, что приращение аргумента  задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее!!!!). Изобразите координатные оси, примерно такой же график функции
задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее!!!!). Изобразите координатные оси, примерно такой же график функции  и точки
и точки  .
.
Отложите на чертеже небольшой отрезок  слева от точки
слева от точки  . При этом точка
. При этом точка  расположится левее точки
расположится левее точки  , а точка
, а точка  – ниже точки
– ниже точки  . Теперь проведите секущую графика функции
. Теперь проведите секущую графика функции  и начните мысленно уменьшать приращение
и начните мысленно уменьшать приращение  вправо к точке
вправо к точке  . В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!
. В результате данная секущая будет стремиться занять положение той же самой «зелёной» касательной!
Примечание: приращение с левой стороны осуществляется «против оси абсцисс» и поэтому отрицательно:  . Заметьте, что всё остаётся корректным, так, в нашем случае соответвующее приращение
. Заметьте, что всё остаётся корректным, так, в нашем случае соответвующее приращение  тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным
тоже меньше нуля, и по этой причине левосторонний предел таки будет положительным  , корректно показывая (как и его правосторонний коллега) рост функции в точке
, корректно показывая (как и его правосторонний коллега) рост функции в точке  . Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.
. Односторонние пределы конечны и совпадают, что говорит о существовании общего предела, производной и единой касательной.
Таким образом, существование производной в точке геометрически очень удобно ассоциировать с существованием ОБЩЕЙ КАСАТЕЛЬНОЙ в данной точке.
Очевидно, что функция не дифференцируема в точках разрыва. Во-первых, она может быть не определена в такой точке, следовательно, приращение  задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела
задать невозможно (на нет и суда нет). А во-вторых, практически всегда попросту не существует общего предела 
Вывод: из дифференцируемости функции в точке  необходимо (обязательно) следует её непрерывность в данной точке.
необходимо (обязательно) следует её непрерывность в данной точке.
Однако обратное утверждение в общем случае неверно, то есть из непрерывности функции дифференцируемость следует далеко не всегда!.
Для нахождения производной от данной функции  необходимо провести следующие действия:
необходимо провести следующие действия:
1) дать аргументу x приращение  , вычислить наращенное значение функции
, вычислить наращенное значение функции 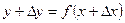 ;
;
2)найти соответствующее приращение функции:  ;
;
3) составить отношение приращения функции к приращению аргумента:  ;
;
4) найти предел данного отношения при 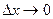 .
.
Таблица производных
1. Производная постоянной равна нулю, т.е. если y=C, где C=const, то  .
.
док-во: y=C, следовательно, при любом значении x 

Доказывая аналогичными способами можно вывести производные всех элементарных функций.
Таблица производных элементарных функций:
1.  6.
6. 
2.  7.
7. 

3. 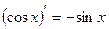
4. 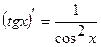 8.
8. 
5.  9.
9. 
Правила дифференцирования.
Теорема 1. Постоянный множитель выносится за знак производной.
Доказательство:

ч.т.д.
Теорема 2.
Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций.

Теорема 3.
Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную от второй,т.е. если

Теорема 4.
Производная частного равна дроби, у которой знаменатель есть квадрат знаменателя исходной дроби,а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателю, т.е.
если  , то
, то  .
.
Пример 1. 

Пример 2.


Пример 3.

Пример 4.

Пример 5.

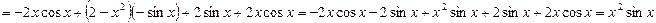
Пример 6.

Д/З Для того, чтобы находить производную функций надо
- Прочитать материал и разобраться, что такое производная функции
- Выучить таблицу производных
- Выучить правила дифференцирования;
- Найдите производные

|

|

|

|

|

|

|
