Ищем приближающую функцию в виде:
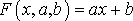
. (11)
Находим частные производные
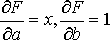
. (12)
Составляем систему вида (8)
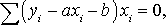
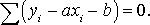
Здесь и далее сумма ведется по переменной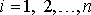 
.
Далее имеем
,
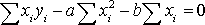
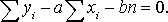
(13)
Разделив каждое уравнение (13) на n, получаем
,
.
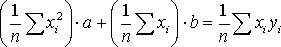
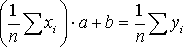
Введем обозначения
.
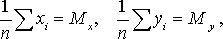
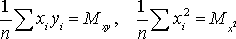
Тогда последняя система будет иметь вид
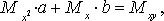
или в матричной форме
.
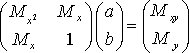
Откуда
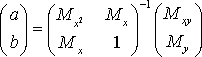
. (14)
Вычислив значения параметров a, b в соответствие с (14), получаем конкретные значения и, следовательно, конкретный вид линейной функции (11).
В случае нахождения приближающей функции в форме квадратного трехчлена имеем:
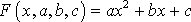
. (15)
Находим частные производные:
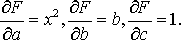
Составляем систему вида (8)
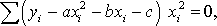
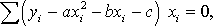
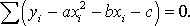
Далее имеем
,
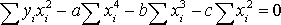
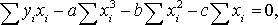
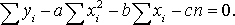
Разделив каждое уравнение на n и перенеся члены, не содержащие неизвестные параметры в правую часть получаем:
,
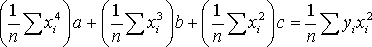
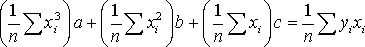
, (16)
.
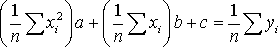
Решив систему (16) относительно неизвестных a, b, c, находим значения параметров приближающей функции.
Найти решение рассмотренной выше задачи регрессии в пакете MATLAB можно другим способом. Для этого следует использовать тот факт, что коэффициенты искомой функции, минимизирующей сумму квадратов отклонений, являются решением переопределенной системы уравнений. Для случая интерполяции полиномом второй степени данных, приведенных выше, система уравнений имеет вид:
.
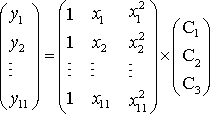
Решение данной системы уравнений, удовлетворяющее методу наименьших квадратов, находится с помощью оператора \:
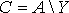
где
, 
.
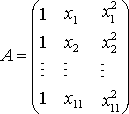
Таким образом, альтернативный подход к нахождению коэффициентов аппроксимирующего полинома реализуются выполнением следующей последовательности команд:
A=[ones(size(X')) X' X'.^2]
A =
1 0 0
1 1 1
1 2 4
1 3 9
1 4 16
1 5 25
1 6 36
1 7 49
1 8 64
1 9 81
1 10 100
C=A\Y'
C =
2.1050e+000
-1.0714e+000
2.0482e-001
Нахождение приближающей функции в виде других элементарных функций
Покажем, что задача нахождение приближающей функции, зависящей от двух параметров, может быть сведена к нахождению параметров линейной функции.
Степенная функция (геометрическая регрессия)
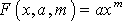
. (17)
Предполагая, что в табл. 1 все значения аргумента и значения функции положительны, прологарифмируем (17), при условии, что a > 0:
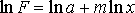
. (18)
Так как функция F является приближающей для функции f, функция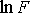 
будет приближающей для функции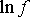 
. Введем новую переменную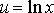 
, тогда, как следует из (18), 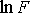будет функцией от u: 
.
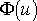
Обозначим
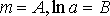
, (19)
тогда (18) принимает вид
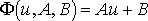
, (20)
т.е. задача свелась к отысканию приближающей функции в виде линейной.
На практике для нахождения приближающей функции в виде степенной используют следующий алгоритм:
1) составляют по заданной табл. 1. новую таблицу, прологарифмировав значения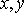 
в исходной таблице;
2) находят по новой таблице параметры A и B приближающей функции вида (20);
3) находят в соответствие с (19) значения параметров a, m.
Показательная функция
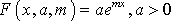
. (21)
Прологарифмировав равенство (21), получим
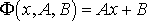
. (22)
Таким образом, задача сведена к предыдущей.
Дробно-линейная функция
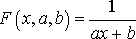
(23)
Перепишем (23) следующим образом:
.
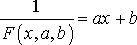
Из последнего равенства следует, что надо составить новую таблицу, заменив в ней значения функции обратными числами. Используя новую таблицу найти a, b и подставить найденные значения параметров в (23).
Логарифмическая функция
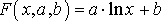
. (24)
Из (24) видно, что для перехода к линейной функции достаточно сделать подстановку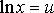 
. Следовательно, для нахождения значений a, b нужно прологарифмировать значения аргумента в исходной таблице (табл. 1) и, рассматривая полученные значения в совокупности с исходными значениями функции, найти для новой таблицы приближающую функцию в виде линейной. Коэффициенты a, b найденной функции подставить в (24).
Гипербола
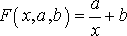
. (25)
Для перехода к линейной функции достаточно сделать подстановку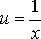 
:
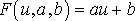
. (26)
Далее заменить значения аргумента обратными числами и найти для новой таблицы приближающую функцию линейного вида (26). Полученные значения параметров подставить в (25).