св-ва бинарных отношений: рефлексивность, симметричность, интисимметричность, транзитивность.
Свойства:
1. R – рефлексивно, если "а: (а;а)ÎR
Тогда в матрице отношения R на главной диагонали стоят только единицы: "i cii=1
2. R – не рефлексивно, если $а: (а;а)ÏR
На главной диагонали матрицы есть хотя бы один ноль.
3. R – антирефлексивно, если "а: (а;а)ÏR
Тогда на главной диагонали матрицы стоят только нули: "i cii=0.
4. R – симметрично, если "а,b: (a;b)ÎR Þ (b;a)ÎR.
 Тогда в матрице отношения "i,j: cij=сji=1. Значит, матрица симметрична относительно главной диагонали. Тогда в матрице отношения "i,j: cij=сji=1. Значит, матрица симметрична относительно главной диагонали.
5. R – не симметрично, если $a,b: (a;b)ÎR и (b;a)ÏR
6. R – антисимметрично, если "a¹b. (a;b)ÎR Þ (b;a)ÏR, т.е. ни для каких различных a и b (a¹b) не выполняется одновременно (a;b)ÎR и (b;a)ÎR. Если же (a;b)ÎR и (b;a)ÎR, то a=b. Тогда в соответствующей матрице отношения ни для каких i,j: i¹j не выполняется Cij=Cji=1. Таким образом, отсутствуют единицы, симметричные относительно главной диагонали.
7. R – транзитивно, если того, что "a,b,c: (a,b)ÎR и (b,c)ÎR следует, что (a,c)ÎR.
В матрице такого отношения должно выполняться след условие: если cij=1 и cjk=1 "i, j, k
Говорят, что в М задано бинарное отношение Т, если М´М есть декартово произведение и в М´М выделено произвольное подмн-во Т. Таким образом, произвольное подмн-во ТÌМ´М есть бинарное отношение.
Мы будем говорить, что эл-т a находится в отношении Т к эл-ту b в том и только в том случае, когда пара (а,b) принадлежит мн-ву Т. Для этого возможны два равносильных способа обозначения: аТb или (а,b)ÎТ.
| 21. Понятие подграфа. Реберно-порожденный подграф. Основные операции над графами.
 Подграфом G1=(V1, А1) графа G =(V, А) наз часть графа, кот сама явл графом. G =(V, А). Пусть V1Ì V и А1Ì А; G1=(V1, А1). G1 явл подграфомóдля " (Xi, Xj)ÎА1 $ верш, инцид ему и Î V1
Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1.
Операции над графами: Подграфом G1=(V1, А1) графа G =(V, А) наз часть графа, кот сама явл графом. G =(V, А). Пусть V1Ì V и А1Ì А; G1=(V1, А1). G1 явл подграфомóдля " (Xi, Xj)ÎА1 $ верш, инцид ему и Î V1
Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1.
Операции над графами:
1) Объединение двух графов G1=(V1, A1) и G2=(V2, A2) есть граф S=(V1ÈV1,A1ÈA2).На рисунке 1 показано объединение двух графов.

| 2) Пересеч. двух графов G1=(V1, A1) и G2=(V2,A2) есть граф S=(V1∩V2,A1∩A2). 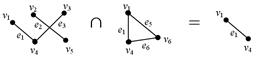
| 3) Кольцевая сумма двух графов G1ÅG2 есть граф, не имеющий изолированных вершин и состоящий только из ребер, присутствующих либо в G1, либо в G2, но не в обоих графах одновременно. Т.о. это Е1ÅЕ2 реберно-порожденный граф. G1ÅG2=(G1 \ G2)È(G2 \ G1)

| 4) Разностью графов G1=(V1, А1) и G2=(V2, А2) наз-ся граф G =(V, А) где А=А1 А2 и
G явл реберно-порожд. подграфом графа G1.
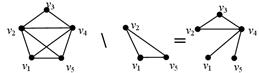
| | 5) Дополнение графа G наз-ся граф G1 с теми же вершинами, что и граф G и с ребрами, кот-е надо добавить к графу G чтобы получить полный граф. Полный граф – все его вершины смежны между собой.
|
|
9. Отношение эквивалентности, определения, примеры. Теоремы о связи разбиения множества и отношением эквивалентности на нем
Бинарное отношение ТÌМ´М называется отношением эквивалентности, заданном на мн-ве М, тогда и только тогда, когда оно удовлетворяет следующим трем усл-виям:
"a, aÎM Þ (a,a)ÎT, т.е. отношение Т удовлетворяет усл-вию рефлексивности
"a"b, aÎM, bÎM если (a,b)ÎT, то (b,a)ÎT, т.е. отношение Т удовлетворяет усл-вию симметричности
"a"b"c, aÎM, bÎM, cÎM если (a,b)ÎT и (b,c)ÎT, то (a,c)ÎT, т.е. отношение Т удовлетворяет усл-вию транзитивности
Таким образом, эквивалентность есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, симметричности и транзитивности.
Отношение равенства чисел есть отношение эквивалентности, т.к. является рефлексивным, симметричным и транзитивным.
А бинарное отношение «<» для чисел не явл отношением эквивалентности, т.к. оно не удовлетворяет условию симетричности.
Разбиение множества. Пусть А — произвольное множество. Семейство 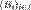 непустых и попарно не пересекающихся множеств называют разбиением множества А, если объединение множеств семейства непустых и попарно не пересекающихся множеств называют разбиением множества А, если объединение множеств семейства 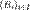 равно А, то есть равно А, то есть 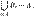 Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.
отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [X]p и [Y]p имеют общий элемент
Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.
отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [X]p и [Y]p имеют общий элемент 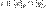 . Тогда . Тогда 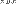 и и 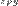 . В силу симметричности отношения P имеем . В силу симметричности отношения P имеем 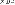 , и тогда , и тогда 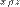 и и 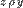 . В силу транзитивности отношения P получим X P Y. Пусть . В силу транзитивности отношения P получим X P Y. Пусть 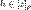 , тогда , тогда 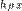 . Так как . Так как 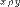 , то , то 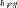 и, следовательно, и, следовательно, 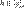 .
Обратно, если .
Обратно, если 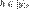 , то в силу симметричности , то в силу симметричности 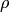 получим получим 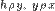 и в силу транзитивности — и в силу транзитивности — 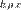 , то есть , то есть 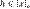 . Таким образом, . Таким образом, 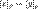 .
Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого .
Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого 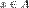 справедливо справедливо 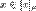 (поскольку (поскольку 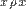 ), т.е. каждый элемент множества A принадлежит некоторому классу эквивалентности по отношению P, то множество всех классов эквивалентности по отношению P образует разбиение исходного множества A. Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.
Теперь пусть ), т.е. каждый элемент множества A принадлежит некоторому классу эквивалентности по отношению P, то множество всех классов эквивалентности по отношению P образует разбиение исходного множества A. Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.
Теперь пусть 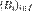 — некоторое разбиение множества — некоторое разбиение множества  . Рассмотрим отношение P, такое, что . Рассмотрим отношение P, такое, что 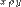 имеет место тогда и только тогда, когда X и Yпринадлежат одному и тому же элементу имеет место тогда и только тогда, когда X и Yпринадлежат одному и тому же элементу 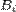 данного разбиения: данного разбиения: 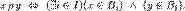 Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых
Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых 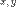 и и  имеет место имеет место 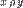 и и 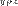 , то , то 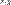 и и  в силу определения отношения в силу определения отношения  принадлежат одному и тому же элементу принадлежат одному и тому же элементу  разбиения. Следовательно, разбиения. Следовательно, 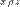 и отношение P транзитивно. Таким образом, P — эквивалентность на A.
31Отношения нестрогого порядка, определения, примеры.
Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "а, аÎМ Þ (а,а)ÎТ, т.е. отношение Т удовлетворяет условию рефлексивности
2) "a"b, aÎМ, bÎМ, если (a,b)ÎТ и (b,a)ÎТ, то a=b, т.е. отношение Т удовлетворяет условию антисимметричности
3) "a"b"c, aÎМ, bÎМ, cÎМ, если (a,b)ÎТ и (b,c)ÎТ, то (a,c)ÎТ, т.е. отношение Т удовлетворяет условию транзитивности
Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности.
Пример 1. Отношение «£» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: а£а; если а£b и b£a, то a=b; если a£b и b£c, то a£c.
Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АÌВ и ВÌА, то А=В, и, наконец, если АÌВ и ВÌС, то АÌС.
Отношения строгого порядка, определения, примеры.
Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "a, aÎM Þ (a,a)ÏT, т.е. отношение Т удовлетворяет усл-вию антирефлексивности
2) "a"b, (a,b) и (b,a) не могут принадлежать Т одновременно, т.е. отношение Т удовлетворяет усл-вию несимметричности
3) "a"b"c, aÎM, bÎM, cÎM если (a,b)ÎT и (b,c)ÎT, то (a,c)ÎT, т.е. отношение Т удовлетворяет усл-вию транзитивности
Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности.
Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a<a, для любых 2х действит чисел a,b либо a<b, либо b<a, и значит, они не могут иметь место одновременно. А для любых 3х чисел: если a<b и b<c, то a<c.
Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка. и отношение P транзитивно. Таким образом, P — эквивалентность на A.
31Отношения нестрогого порядка, определения, примеры.
Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "а, аÎМ Þ (а,а)ÎТ, т.е. отношение Т удовлетворяет условию рефлексивности
2) "a"b, aÎМ, bÎМ, если (a,b)ÎТ и (b,a)ÎТ, то a=b, т.е. отношение Т удовлетворяет условию антисимметричности
3) "a"b"c, aÎМ, bÎМ, cÎМ, если (a,b)ÎТ и (b,c)ÎТ, то (a,c)ÎТ, т.е. отношение Т удовлетворяет условию транзитивности
Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности.
Пример 1. Отношение «£» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: а£а; если а£b и b£a, то a=b; если a£b и b£c, то a£c.
Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АÌВ и ВÌА, то А=В, и, наконец, если АÌВ и ВÌС, то АÌС.
Отношения строгого порядка, определения, примеры.
Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "a, aÎM Þ (a,a)ÏT, т.е. отношение Т удовлетворяет усл-вию антирефлексивности
2) "a"b, (a,b) и (b,a) не могут принадлежать Т одновременно, т.е. отношение Т удовлетворяет усл-вию несимметричности
3) "a"b"c, aÎM, bÎM, cÎM если (a,b)ÎT и (b,c)ÎT, то (a,c)ÎT, т.е. отношение Т удовлетворяет усл-вию транзитивности
Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности.
Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a<a, для любых 2х действит чисел a,b либо a<b, либо b<a, и значит, они не могут иметь место одновременно. А для любых 3х чисел: если a<b и b<c, то a<c.
Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка.
| 22. Числовые характеристики графа: цикломатическое число, хроматическое число. Раскраска графов.
Цикломатическим числом ν(G) графа G наз. наименьшее число ребер, удаление которых приводит к графу без циклов; ν(G) =m-n+k. где т - число ребер, n - число вершин, k - число компонент связности графа G.
Хроматическим числом χ(G) наз. наименьшее количество цветов, которыми можно раскрасить вершины графа G так, чтобы любые смежные вершины были окрашены разными цветами.
Правила раскраски графов:
1) Раскрашиваем вершины графа
2) 2 смежные вершины – разного цвета
3) Экономим краски.
4) Начинаем раскрашивать с….
|
| 10. Упорядоченные мн-ва, определения, примеры.
Два эл-та aÎM и bÎM являются сравнимыми в данном порядке TÌM´M, если про них можно сказать, что (a,b)ÎT или (b,a)ÎT, или a=b.
Мн-во М с введенным порядком Т является упорядоченным (линейно упорядоченным), если любые два эл-та этого мн-ва являются сравнимыми.
Про мн-во М, на котором просто введен некоторый порядок Т, т.е. в котором существуют сравнимые эл-ты, говорят, что оно частично упорядоченно.
Св-вом упорядоченности обладает мн-во всех точек на действительной числовой прямой R, т.к. любые два действительных числа можно сравнить между собой.
Для отношения «быть собственным подмн-вом» это св-во не имеет места, т.к. по отношению включения можно сравнить далеко не все подмн-ва. Например, числовой интервал (-2,5) нельзя сравнить с отр-ком [0,7] по отношению включения. Таким образом, это мн-во является частично упорядоченным.
Среди линейно упорядоченных мн-в выделяют вполне упорядоченные мн-ва. Для его определения введем определение усл-вия минимальности.
Говорят, что мн-во М удовлетворяет усл-вию миним-ти для некот отн-ния порядка Т, если в люб его непуст подмн-ве XÌM существует такой эл-т a, что "x xÎX, имеет место: аТх.
Итак, мн-во назыв вполне упоряд-ым, если оно явл лин упоряд-ым и удовлетворяет усл-вию миним-ти. Например, мн-во натур чисел явл вполне упоряд-ым, а мн-во действит чисел не явл вполне упорядоченным, т.к. для интервалов не сущ-ет минимального эл-та.
Обратим внимание на то, что одно и то же мн-во может быть линейно упорядоченным относительно одного порядка и лишь частично упорядоченным относительно другого. Например, мн-во людей с введенным отн-ем старшинства явл лин упоряд-ным (роль рав-ва играет отн-ние «быть ровесниками»), а это же мн-во с отн-нием «быть предком» не явл лин упоряд-ным, т.к. про любых 2х людей нельзя сказать, что один явл-ся предком другого.
| 34 Операции над бинарными отношениями
Так как отношения на Х задаются подмножествами rНXґY, для них определимы те же операции, что и над множествами:
1. Объединение r1Иr2: r1Иr2={(х, у)| (х, у)Оr1 или (х, у)Оr2}.
2. Пересечение r1Зr2: r1Зr2={(х, у)| (х, у)Оr1 и (х, у)Оr2}.
3. Разность r1\r2: r1\r2={(х, у)| (х, у)Оr1 и (х, у)П r2}.
4. Дополнение 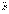 : : 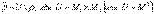 .
5. Обратное отношение r -1: х r -1 у тогда и только тогда, когда уrх, r -1={(x, y)| (y, x)Оr}.
Пример 13.
Если r - «быть моложе», то r -1 – «быть старше».
6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2.
7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b.
Пример 14.
Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии». .
5. Обратное отношение r -1: х r -1 у тогда и только тогда, когда уrх, r -1={(x, y)| (y, x)Оr}.
Пример 13.
Если r - «быть моложе», то r -1 – «быть старше».
6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2.
7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b.
Пример 14.
Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии».
|
11. Деревья, лексикографический порядок, определения, примеры.
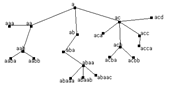
Имеем некот алфавит. Заметим, что его мощность должна быть не меньше, чем макс число ветвлений в некот вершине дерева. Не ограничивая области, возьмем латин алфавит. Дерево в мате-ке строится сверху вниз. Пусть корень (начальная вершина) дерева назыв a. Тогда в 1ом ярусе самая лев вер-на есть аа, след – ab, затем – ac и т.д., во 2ом ярусе вер-ны, выход из вер-ны aa, имеют названия aaa, aab, aac и т.д., вер-ны, выход из вер-ны ab, имеют названия aba, аbb, аbc и т.д. Таким образом, вер-на, находящаяся в n-м ярусе, имеет названия длины n. Если из вер-ны не выходит ни одной ветви, то она называется концевой.
Пример. В дереве естественным образом устанавливается отн-ние предшествования: одна вер-на предшествует др, если ее имя явл префиксом имени 2ой вер-ны. Так, вершина aa предшествует вер-не aabab. В этом порядке сравнимые вер-ны на 1ой ветви: та, которая находится выше, предшеств той, кот находится ниже. Такой порядок графич иллюстрирует соотн-ние между людьми «быть предком»; вер-ны, располож выше, изображают предка, а вер-ны, располож ниже, - потомков. Если рассматривать дерево на рис как генеал-кое, то аа есть прадед aabab. Разумеется, в этом порядке вер-ны дерева не представляют собой упоряд мн-ва, а лишь частич упоряд мн-во, т.к. вер-ны aaa и ababb не сравнимы.
1) если имя 1ой является префиксом имени 2ой.
2)  Если все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab.
В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным».
Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
1) если имя первой явл префиксом имени 2ой
2) выделяется макс общ префикс 2х имен и далее, если след за макс общ префиксом буква имени 1ой вер-ны расположена раньше, чем такая же буква имени 2ой вершины.
Этот порядок называется лексикографическим, алфавитным или словарным. Если все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab.
В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным».
Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
1) если имя первой явл префиксом имени 2ой
2) выделяется макс общ префикс 2х имен и далее, если след за макс общ префиксом буква имени 1ой вер-ны расположена раньше, чем такая же буква имени 2ой вершины.
Этот порядок называется лексикографическим, алфавитным или словарным.
| 23. Задачи о кратчайших путях: путь с наим. числом дуг, (путь кратчайшей длины).
Путь наз кратчайшим, если он содержит наименьшее число дуг из всех возможных.
Алгоритм построения наименьшего пути от верш а к верш b.
1. Присвоить верш а метку 0
2. Если вершина Х ≠ а и верш Х – смежна с а, то присвоить верш Х метку 1.
3. Пусть V(m) – мн-во верш, им-х метку m. Тогда V(m+1) – мн-во верш
{x | $ y, y Î V(m)} где х и у смежны.
4. Процесс присвоения прекратить, как только метку получила вершина b.
5. Рассм послед-ть вершин от верш b {Xi1ÎV(n); Xi2 смежн с Х i1 и Xi2ÎV(n-1);…а=Хim}, Þ {a=Хim, Х(im-1)… Хi1=b} – путь из вершины а в вершину b
|
| 12. Св-ва отображения, ф-ции графики. Ф-ции как част случай бинар отношений.
Функцией называется функциональное соответствие. Если функция ¦ устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип А®В (обозначается ¦: А®В). Каждому элементу а из области определения функция ¦ ставит в соответствие элемент b из области значений. Это обозначается ¦(а)=b. Элемент а – аргумент функции, элемент b – значение функции на а.
Отображением. А в называется всюду определённая функция. __ А®В.
Отображением А на В называется всюду определённое и при этом сюръективное функциональное соответствие ¦: А®В.
Отображением типа А®А часто называют преобразованием множества А. Функция типа А®А, являющаяся отображением А на А, называется перестановкой на А.
Функции ¦ и g равны, если:
- Их области определения – одно и то же множество А
- Для любого аÎА ¦(а)=g(а).
Функция типа ¦:А1´А2´…´Аn®B назывется n-местной. В этом случае принято считать, что функция имеет n аргументов: ¦(а1……аn)=b, где а1ÎА1,……..,аnÎAn, bÎB.
Если соответствие, обратное к функции ¦: А®В, является функциональным, то оно называется функцией, обратной к ¦ (обозначается ¦-1). Для функции ¦: А®В обратная функция существует тогда и только тогда, когда ¦ является взаимно однозначным соответствием между своими областями определения и значений.
Способы задания функции:
- Графиком
- Таблицей
- Формулой, описывающей функцию, как суперпозициюдругих (исходных) функций.
- Рекурсивной вычислительной процедурой. Например, функция ¦(х)=1*2*3….*(х – 1)*х=х! Описывается рекурсивной вычислительной процедурой, задаваемой следующими правилами: ¦(0)=1; ¦(х+1)= ¦(х)*(х+1)
Если элемент а принадлежит множеству М, то соответствующий ему элемент d=¦(a) называется его образом. Каждый элемент а может иметь единственный образ, при этом для b может существовать не один элемент из М, образом котрого он является.
Совокупност всех тех эл-тов а из М, образом которых является данный элемент b из N, называется прообразом или полным прообразом элемента b и обозначается ¦-1(b).
| 24. Теорема об эйлеровом цикле.
Эйлеров цикл – сод-т все ребра графа и ни по одному нельзя пройти 2-ды.
Теоp.Эйлеров цикл в связном графе $ ó когда все вершины имеют четную степень.
Док-во. Необход-ть условия очевидна, так как при каждом прохожд цикла через к-либо вершину использ. 2 ребра - по 1 из них маршрут входит в верш, по др вых-т из нее (это относ. и к старт верш - в ней ведь маршрут должен закон-ся). Достаточность.
Пусть G - связн граф, в кот-м > 1 верш и степени всех вершин четны. Значит, степень каждой вершины >= 2, поэтому по теореме (критер прост цикла) в графе G имеется цикл Z1. Если удалить все ребра этого цикла из графа G, то пол-ся граф G1, в кот-м степени вершин также четны. Если в G1 нет ни одного ребра, то Z1- эйлеров цикл. В прот случае, применяя ту же теорему к графу, получ из G1 удалением всех изолир-х верш, заключаем, что в G1 имеется цикл Z2. Удалив из G1 все ребра цикла Z2, получим граф G2. Продолжая действовать т. о., пока не придем к пустому графу, получим в итоге систему циклов Z1….Zk, причем каждое ребро графа Î в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов Z1…Zk-1 имеет общую вершину с Zk. Допустим, для определенности, что таков цикл Zk-1. Пусть 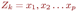 , , 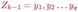 , и Xi =Yj для некоторых i и j. Тогда посл-ть вершин , и Xi =Yj для некоторых i и j. Тогда посл-ть вершин 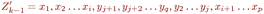 очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности Î одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым. очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности Î одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым.
|
| 13. Свойства функций: инъективность, сюрьективность, биективность.
1.Функция f называется инъективной(или, коротко, инъекция), если разным элементам множества X сопоставлены разные элементы множества Y. Более формально, функция f инъективна, если для любых двух элементов X1, X2 Î X таких, что f(x1) = f(x2), непременно выполняется x1 = x2.
Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть, при инъекции не бывает так, чтобы два или больше разных элементов X отображались в один и тот же элемент Y. А при сюръекции не бывает так, чтобы какой-то элемент Y не имел прообраза.
2.Функция f называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция fсюръективна, если образ множества X при отображении совпадает с множеством Y: f[X] = Y.
Такое отображение называется ещё отображением на.
Если условие сюръективности нарушается, то такое отображение называют отображением в.
3.Если функция является и сюръективной, и инъективной, то такую функцию называют биективной или взаимно однозначной.
| 24 Алгоритм построения эйлерова цикла.
Цикл называется эйлеровым, если ему принадлежат все ребра (и ни по одному ребру нельзя пройти дважды)
выбрать произвол вел-ну а
выбрать произвольно некоторое ребро, инцидентное а, и присвоить ему №1
каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего ребра
находясь в некоторой вер-не х, не выбирать ребра, инцидентного а, если есть возможность другого выбора
находясь в вер-не х, не выбирать мостов
После того, как все ребра занумерованы m={1,2,…,n} – есть путь, образующий эйлеров цикл.
|
 Тогда в матрице отношения "i,j: cij=сji=1. Значит, матрица симметрична относительно главной диагонали.
Тогда в матрице отношения "i,j: cij=сji=1. Значит, матрица симметрична относительно главной диагонали. Подграфом G1=(V1, А1) графа G =(V, А) наз часть графа, кот сама явл графом. G =(V, А). Пусть V1Ì V и А1Ì А; G1=(V1, А1). G1 явл подграфомóдля " (Xi, Xj)ÎА1 $ верш, инцид ему и Î V1
Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1.
Операции над графами:
Подграфом G1=(V1, А1) графа G =(V, А) наз часть графа, кот сама явл графом. G =(V, А). Пусть V1Ì V и А1Ì А; G1=(V1, А1). G1 явл подграфомóдля " (Xi, Xj)ÎА1 $ верш, инцид ему и Î V1
Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1.
Операции над графами:




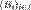 непустых и попарно не пересекающихся множеств называют разбиением множества А, если объединение множеств семейства
непустых и попарно не пересекающихся множеств называют разбиением множества А, если объединение множеств семейства 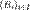 равно А, то есть
равно А, то есть 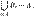 Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.
отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [X]p и [Y]p имеют общий элемент
Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.
отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [X]p и [Y]p имеют общий элемент 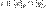 . Тогда
. Тогда 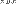 и
и 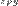 . В силу симметричности отношения P имеем
. В силу симметричности отношения P имеем 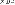 , и тогда
, и тогда 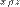 и
и 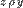 . В силу транзитивности отношения P получим X P Y. Пусть
. В силу транзитивности отношения P получим X P Y. Пусть 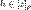 , тогда
, тогда 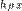 . Так как
. Так как 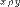 , то
, то 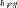 и, следовательно,
и, следовательно, 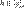 .
Обратно, если
.
Обратно, если 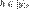 , то в силу симметричности
, то в силу симметричности 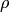 получим
получим 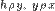 и в силу транзитивности —
и в силу транзитивности — 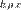 , то есть
, то есть 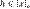 . Таким образом,
. Таким образом, 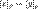 .
Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого
.
Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого 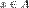 справедливо
справедливо 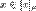 (поскольку
(поскольку 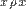 ), т.е. каждый элемент множества A принадлежит некоторому классу эквивалентности по отношению P, то множество всех классов эквивалентности по отношению P образует разбиение исходного множества A. Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.
Теперь пусть
), т.е. каждый элемент множества A принадлежит некоторому классу эквивалентности по отношению P, то множество всех классов эквивалентности по отношению P образует разбиение исходного множества A. Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.
Теперь пусть 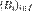 — некоторое разбиение множества
— некоторое разбиение множества  . Рассмотрим отношение P, такое, что
. Рассмотрим отношение P, такое, что 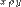 имеет место тогда и только тогда, когда X и Yпринадлежат одному и тому же элементу
имеет место тогда и только тогда, когда X и Yпринадлежат одному и тому же элементу 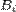 данного разбиения:
данного разбиения: 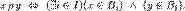 Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых
Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых 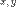 и
и  имеет место
имеет место 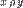 и
и 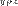 , то
, то 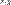 и
и  в силу определения отношения
в силу определения отношения  принадлежат одному и тому же элементу
принадлежат одному и тому же элементу  разбиения. Следовательно,
разбиения. Следовательно, 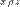 и отношение P транзитивно. Таким образом, P — эквивалентность на A.
31Отношения нестрогого порядка, определения, примеры.
Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "а, аÎМ Þ (а,а)ÎТ, т.е. отношение Т удовлетворяет условию рефлексивности
2) "a"b, aÎМ, bÎМ, если (a,b)ÎТ и (b,a)ÎТ, то a=b, т.е. отношение Т удовлетворяет условию антисимметричности
3) "a"b"c, aÎМ, bÎМ, cÎМ, если (a,b)ÎТ и (b,c)ÎТ, то (a,c)ÎТ, т.е. отношение Т удовлетворяет условию транзитивности
Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности.
Пример 1. Отношение «£» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: а£а; если а£b и b£a, то a=b; если a£b и b£c, то a£c.
Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АÌВ и ВÌА, то А=В, и, наконец, если АÌВ и ВÌС, то АÌС.
Отношения строгого порядка, определения, примеры.
Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "a, aÎM Þ (a,a)ÏT, т.е. отношение Т удовлетворяет усл-вию антирефлексивности
2) "a"b, (a,b) и (b,a) не могут принадлежать Т одновременно, т.е. отношение Т удовлетворяет усл-вию несимметричности
3) "a"b"c, aÎM, bÎM, cÎM если (a,b)ÎT и (b,c)ÎT, то (a,c)ÎT, т.е. отношение Т удовлетворяет усл-вию транзитивности
Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности.
Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a<a, для любых 2х действит чисел a,b либо a<b, либо b<a, и значит, они не могут иметь место одновременно. А для любых 3х чисел: если a<b и b<c, то a<c.
Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка.
и отношение P транзитивно. Таким образом, P — эквивалентность на A.
31Отношения нестрогого порядка, определения, примеры.
Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "а, аÎМ Þ (а,а)ÎТ, т.е. отношение Т удовлетворяет условию рефлексивности
2) "a"b, aÎМ, bÎМ, если (a,b)ÎТ и (b,a)ÎТ, то a=b, т.е. отношение Т удовлетворяет условию антисимметричности
3) "a"b"c, aÎМ, bÎМ, cÎМ, если (a,b)ÎТ и (b,c)ÎТ, то (a,c)ÎТ, т.е. отношение Т удовлетворяет условию транзитивности
Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности.
Пример 1. Отношение «£» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: а£а; если а£b и b£a, то a=b; если a£b и b£c, то a£c.
Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АÌВ и ВÌА, то А=В, и, наконец, если АÌВ и ВÌС, то АÌС.
Отношения строгого порядка, определения, примеры.
Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:
1) "a, aÎM Þ (a,a)ÏT, т.е. отношение Т удовлетворяет усл-вию антирефлексивности
2) "a"b, (a,b) и (b,a) не могут принадлежать Т одновременно, т.е. отношение Т удовлетворяет усл-вию несимметричности
3) "a"b"c, aÎM, bÎM, cÎM если (a,b)ÎT и (b,c)ÎT, то (a,c)ÎT, т.е. отношение Т удовлетворяет усл-вию транзитивности
Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности.
Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a<a, для любых 2х действит чисел a,b либо a<b, либо b<a, и значит, они не могут иметь место одновременно. А для любых 3х чисел: если a<b и b<c, то a<c.
Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка.
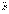 :
: 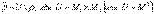 .
5. Обратное отношение r -1: х r -1 у тогда и только тогда, когда уrх, r -1={(x, y)| (y, x)Оr}.
Пример 13.
Если r - «быть моложе», то r -1 – «быть старше».
6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2.
7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b.
Пример 14.
Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии».
.
5. Обратное отношение r -1: х r -1 у тогда и только тогда, когда уrх, r -1={(x, y)| (y, x)Оr}.
Пример 13.
Если r - «быть моложе», то r -1 – «быть старше».
6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2.
7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b.
Пример 14.
Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии».
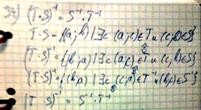
 Если все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab.
В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным».
Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
1) если имя первой явл префиксом имени 2ой
2) выделяется макс общ префикс 2х имен и далее, если след за макс общ префиксом буква имени 1ой вер-ны расположена раньше, чем такая же буква имени 2ой вершины.
Этот порядок называется лексикографическим, алфавитным или словарным.
Если все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab.
В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным».
Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
1) если имя первой явл префиксом имени 2ой
2) выделяется макс общ префикс 2х имен и далее, если след за макс общ префиксом буква имени 1ой вер-ны расположена раньше, чем такая же буква имени 2ой вершины.
Этот порядок называется лексикографическим, алфавитным или словарным.
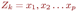 ,
, 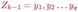 , и Xi =Yj для некоторых i и j. Тогда посл-ть вершин
, и Xi =Yj для некоторых i и j. Тогда посл-ть вершин 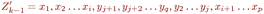 очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности Î одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым.
очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности Î одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым.