Раздел V. УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ И МЕТОДЫИХ РЕШЕНИЯ
Лекция 4. ИССЛЕДОВАНИЕ УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ.
Пусть задана непрерывная функция f (x) и требуется найти все или некоторые корни уравнения
f (x) = 0.
Эта задача распадается на несколько задач. Во-первых, надо исследовать количество, характер и расположение корней. Во-вторых, найти приближенные значения корней. В-третьих, выбрать из них интересующие нас корни и вычислить их с требуемой точностью.
Первая и вторая задачи решаются аналитическими и графическими методами. Например, многочлен

имеет n комплексных корней, не обязательно различных, и все корни лежат внутри круга

Правда, эта оценка не оптимальная; модули всех корней могут быть много меньше правой части неравенства, в чем легко убедиться на примере многочлена

Когда ищутся только действительные корни уравнения полезно составить таблицу значений f (x). Если в двух соседних узлах таблицы функция имеет разные знаки, то между этими узлами лежит нечетное число корней уравнения (по крайней мере, один). Если эти узлы близки, то, скорее всего, корень между ними только один. Но выявить по таблице корни четной кратности сложно.
По таблице можно построить график функции у = f (x) и графически найти точки его пересечения с осью абсцисс. Этот способ более нагляден и дает неплохие приближенные значения корней.
Во многих задачах техники такая точность уже достаточна. В технике еще популярны графические методы решения уравнений (номография). Построение графика зачастую позволяет выявить даже корни четной кратности.
Для того чтобы графически определить корни иногда удается заменить уравнение f (x) = 0 эквивалентным ему уравнением  , в котором функции
, в котором функции  и
и  имеют несложные графики. Например, уравнение
имеют несложные графики. Например, уравнение  удобно преобразовать к виду
удобно преобразовать к виду  Абсциссы точек пересечения этих графиков будут корнями исходного уравнения.
Абсциссы точек пересечения этих графиков будут корнями исходного уравнения.
Приближенные значения корней уточняются различными итерационными методами. Рассмотрим наиболее эффективные из них.
Дихотомия (деление пополам)
Пусть мы нашли такие точки х 0, х 1, что 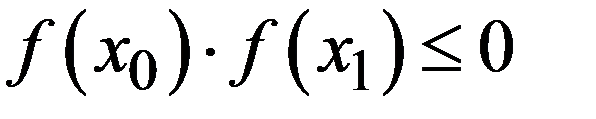 , т.е. нашли отрезок
, т.е. нашли отрезок 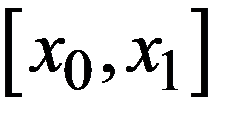 , на котором лежит не менее одного корня уравнения. Найдем середину отрезка х 2 = (х 0 + х 1)/2 и вычислим f (x 2). Из двух половин отрезка выберем ту, для которой
, на котором лежит не менее одного корня уравнения. Найдем середину отрезка х 2 = (х 0 + х 1)/2 и вычислим f (x 2). Из двух половин отрезка выберем ту, для которой  , ибо один из корней лежит на этой половине.
, ибо один из корней лежит на этой половине.
| q (x) |
| q (x) |
| х 1 |
| х 4 |
| х 0 |
| х 2 |
| х 3 |
| Рис. 16.1 |
 х х |
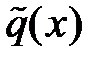 х х
|

|
| х |
| Рис. 16.2 |
Затем новый отрезок опять делим пополам и выберем ту половину, на концах которой функция имеет разные знаки и т.д. (рис. 16.1).
Если требуется найти корень с точностью 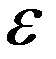 , то продолжаем деление пополам до тех пор, пока длина отрезка даст значение корня с требуемой точностью.
, то продолжаем деление пополам до тех пор, пока длина отрезка даст значение корня с требуемой точностью.
Дихотомия проста и очень надежна: к простому корню она сходится для любых непрерывных функций  , в том числе недифференцируемых, при этом она устойчива к ошибкам округления. Скорость сходимости невелика: за одну итерацию точность увеличивается примерно вдвое, т.е. уточнение трех цифр требует 10 итераций. Зато точность ответа гарантируется.
, в том числе недифференцируемых, при этом она устойчива к ошибкам округления. Скорость сходимости невелика: за одну итерацию точность увеличивается примерно вдвое, т.е. уточнение трех цифр требует 10 итераций. Зато точность ответа гарантируется.
Перечислим недостатки метода. Для начала расчета надо найти отрезок, на котором функция меняет знак. Если в этом отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс (хотя к одному из них сойдется). Метод неприменим к корням четной кратности. Наконец, на системы уравнений дихотомия не обобщается.
Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна.
Удаление корней
Один из недостатков дихотомии – сходимость неизвестно к какому корню, имеется почти у всех итерационных методов. Его можно устранить удалением уже найденного корня.
Если  есть простой корень уравнения
есть простой корень уравнения  и функция
и функция  Липшиц – непрерывна, то вспомогательная функция
Липшиц – непрерывна, то вспомогательная функция  непрерывна, причем все нули функций
непрерывна, причем все нули функций  и
и  совпадают, за исключением
совпадают, за исключением  , ибо (
, ибо (
 . Если же
. Если же 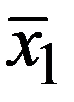 - кратный корень уравнения
- кратный корень уравнения  , то он будет нулем
, то он будет нулем  кратности на единицу меньше; остальные нули обеих функций по-прежнему будут одинаковы. Поэтому найденный корень можно удалить, т.е. перейти к функции
кратности на единицу меньше; остальные нули обеих функций по-прежнему будут одинаковы. Поэтому найденный корень можно удалить, т.е. перейти к функции  . Тогда нахождение остальных нулей функции
. Тогда нахождение остальных нулей функции  сведется к нахождению нулей функции
сведется к нахождению нулей функции  . Когда мы найдем какой-нибудь корень
. Когда мы найдем какой-нибудь корень  функции
функции  , то этот корень тоже можно удалить, вводя новую вспомогательную функцию
, то этот корень тоже можно удалить, вводя новую вспомогательную функцию
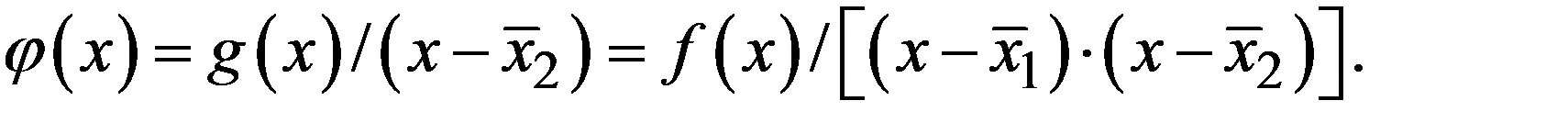 Так можно последовательно найти все корни
Так можно последовательно найти все корни  .
.
Метод простых итераций
Заменим уравнение  эквивалентным ему уравнением
эквивалентным ему уравнением  . Это можно сделать многими способами, например, положив
. Это можно сделать многими способами, например, положив  где
где  - произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение
- произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение  и вычислим дальнейшие приближения по формулам:
и вычислим дальнейшие приближения по формулам:
 .
.
Для преобразования уравнения  к виду
к виду  можно воспользоваться следующей процедурой. Используя нулевое приближение
можно воспользоваться следующей процедурой. Используя нулевое приближение  , найденное, например, графическим путем, заменим уравнение
, найденное, например, графическим путем, заменим уравнение  эквивалентным ему уравнением
эквивалентным ему уравнением 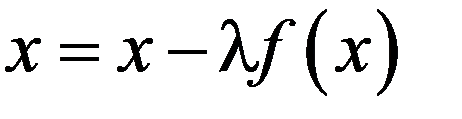 , где число
, где число 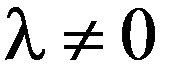 выбирается так, чтобы функция
выбирается так, чтобы функция  была малой по абсолютной величине в окрестности точки
была малой по абсолютной величине в окрестности точки  . Например, можно положить
. Например, можно положить  .
.
Очевидно, если  стремится к некоторому пределу
стремится к некоторому пределу  , то этот предел есть корень исходного уравнения.
, то этот предел есть корень исходного уравнения.
Исследуем условия сходимости. Если  имеет непрерывную производную, тогда
имеет непрерывную производную, тогда  где точка
где точка 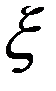 лежит между точками
лежит между точками  и
и  . Поэтому если всюду
. Поэтому если всюду  то отрезки
то отрезки  убывают не медленней членов геометрической прогрессии со знаменателем q <1 и последовательность
убывают не медленней членов геометрической прогрессии со знаменателем q <1 и последовательность  сходится при любом нулевом приближении.
сходится при любом нулевом приближении.
Если 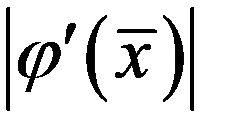 > 1, то в силу непрерывности
> 1, то в силу непрерывности  больше единицы и в некоторой окрестности корня; в этом случае итерации не могут сходиться. Если
больше единицы и в некоторой окрестности корня; в этом случае итерации не могут сходиться. Если  < 1, но вдали от корня
< 1, но вдали от корня  > 1, то итерации сходятся, если нулевое приближение выбрано достаточно близко к корню; при произвольном нулевом приближении сходимости может не быть.
> 1, то итерации сходятся, если нулевое приближение выбрано достаточно близко к корню; при произвольном нулевом приближении сходимости может не быть.
Очевидно, что чем меньше q, тем быстрее сходимость. Вблизи корня асимптотическая сходимость определяется величиной  и будет особенно быстрой при
и будет особенно быстрой при  .
.
Значит успех метода зависит от того, насколько удачно выбрано  . Например, для извлечения квадратного корня, т.е. решения уравнения
. Например, для извлечения квадратного корня, т.е. решения уравнения 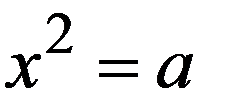 , можно положить
, можно положить  , или
, или 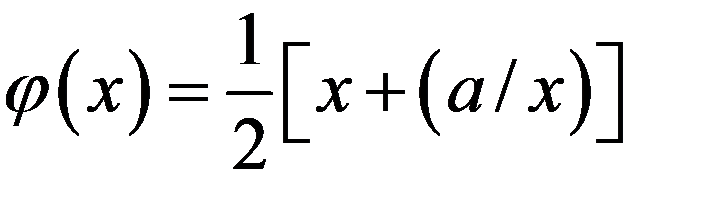 и соответственно написать такие итерационные процессы:
и соответственно написать такие итерационные процессы:  или
или 
Первый процесс вообще не сходится, а второй сходится при любом  ; сходится он очень быстро, ибо
; сходится он очень быстро, ибо  Действительно
Действительно
 но
но 
Второй процесс используют при извлечении корня на клавишных машинах.
Каков практический критерий сходимости, т.е. когда надо прекращать итерации. Из  видно, что если
видно, что если  , то итерации попеременно оказываются то с одной то с другой стороны корня, так что корень заключён в интервале
, то итерации попеременно оказываются то с одной то с другой стороны корня, так что корень заключён в интервале  . Это надёжная, хотя и несколько грубая оценка, но она неприменима при
. Это надёжная, хотя и несколько грубая оценка, но она неприменима при  когда итерации сходятся к корню монотонно, т.е. с одной стороны.
когда итерации сходятся к корню монотонно, т.е. с одной стороны.
Вблизи корня итерации сходятся примерно как геометрическая прогрессия со знаменателем  Чтобы сумма дальнейших ее членов не превосходила
Чтобы сумма дальнейших ее членов не превосходила  , должен выполнятся критерий сходимости
, должен выполнятся критерий сходимости

При выполнении этого условия итерации можно прекращать.
Метод простых итераций и почти все другие итерационные методы имеют важное достоинство: в них не накапливаются ошибки вычислений. Ошибка вычислений эквивалентна некоторому ухудшению очередного приближения. Но это отразится только на числе итераций, а не на точности окончательного результата.