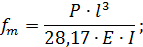
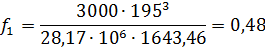
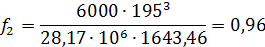
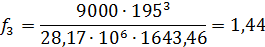
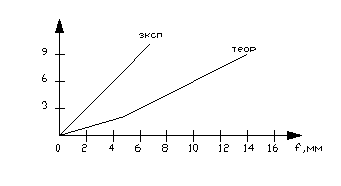
Рис.4. График прогибов балки
ВЫВОД: Экспериментальная величина прогиба значительно меньше расчетной величины вследствие в рассматриваемых конструкциях создается запас прочности (Кзапаса=0,9).
Контрольные вопросы
1. Что такое клей?
2. Назовите основные требования к клеям, применяемым в несущих строительных конструкциях?
3. Какие клеи следует применять в несущих конструкциях?
4. Что вызывает внутренние напряжения в клеевых швах?
5. Какие размеры по ширине и толщине досок рекомендуются при изготовлении клеедощатых конструкций?
6. Какая максимальная влажность древесины допускается при склеивании досок?
7. Почему ограничиваются размеры досок и влажность древесины при изготовлении клеедощатых конструкций?
8. Как определяется несущая способность двутавровой клееной балки?
9. Как определяются теоретические значения напряжений в поперечном сечении балки?
10. Для чего в лабораторной работе используется индикатор часового
типа?
11. Для чего в лабораторной работе используются тензодатчики?
12. Что такое коэффициент безопасности?
13. Что такое разрушающая нагрузка?
14. Почему нагрузка на образец прикладывается в виде двух сосредоточенных сил?
15. Как определяются экспериментальные значения напряжений в поперечном сечении балки?
16. Какой метод принят для расчета деревянных конструкций, его сущность?
17. Как определить модуль упругости клееной древесины при изгибе?
18. Как экспериментально определяются нормальные напряжения в балке при изгибе?
19. Какие формы разрушения могут быть в клеедощатой балке?
20. Почему экспериментальные данные отличаются от теоретических?
Т.к. древесина анизотропная и имеет пороки, а теоретические данные получены для идеализированного материала.
|
|
Лабораторная работа 4
МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ ДЕРЕВЯННЫХ БАЛОК
ЦЕЛЬНОГО И СОСТАВНОГО СЕЧЕНИЯ
Цель работы -определение несущей способности и деформативности деревянных балок цельного и составного сечения при статическом поперечном изгибе.
1. Основные понятия
В изгибаемом элементе от нагрузок, действующих поперек его про-
дольной оси, возникает изгибающий момент и поперечная сила. При этом в сечениях элемента возникают деформации и напряжения изгиба.
Изгибаемые элементы рассчитываются по несущей способности - прочности на действие изгибающего момента и поперечной силы от расчетных нагрузок и по прогибам от нормативных нагрузок. Прочность и жесткость изгибаемых элементов (балок) зависит от размеров и форм поперечных сечений, определяющих их геометрические характеристики: момент инерции I, момент сопротивления W и статический момент S. Прочность изгибаемых элементов рассчитывают по формуле:
(1)
где Wp - расчетный момент сопротивления; М - максимальный изгибающий момент; Rи - расчетное сопротивление древесины изгибу.
Расчет изгибаемого элемента по прогибам заключается в определении его наибольшего прогиба от нормативных нагрузок и сравнении его значения с предельным, допустимым нормами проектирования, т.е.
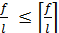пред. (2)
Приборы и принадлежности: нагрузочное рычажное устройство; ин-дикатор часового типа с ценой деления 0,01 мм; штангенциркуль с точно-стью измерения до 0,1 мм; образцы - балки составного и цельного сечения; штатив для индикатора; грузы.
|
|
3. Подготовительные работы
Для проведения механических испытаний на статический изгиб используют балки цельного и составного сечения (рис.1, 2). Правильность и точность подготовленных к испытанию образцов проверяют угольником и измерительной линейкой.
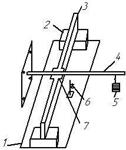
Рис.1. Схема испытания балок на изгиб:
1 – стол; 2 – опорная подушка; 3 – испытуемая балка; 4 – рычаг; 5 – грузы; 6 – индикатор, установленный на штативе; 7 – центрируемая балка
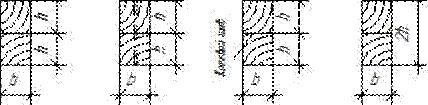
а б в г
Рис.2. Типы составных балок для испытания на изгиб:
а – без связей; б – на гвоздях; в – на клею; г – цельного сечения
Механические испытания балок цельного и составного сечения производят на стенде по схеме (см.рис.3 а, б).
а б
Рис.3. Схемы испытания древесины на статический изгиб:
а- при нагружении в одной точке посредине расстояния между опорами;
б- при нагружении в двух точках на одной трети расстояния от опор
Нагрузочным устройством служит рычаг с отношением плеч 1:6, что позволяет небольшими грузами 41,6 Н создавать ступени нагружения по 250 Н. Измерение прогибов балок выполняют индикаторами часового типа с ценой деления 0,01 мм. Испытывают четыре типа балок цельного и составного сечений. Полученные данные эксперимента сравнивают с результатами теоретического расчета.
4. Экспериментальная часть
Порядок выполнения работы. Механические испытания балокцельного и составного сечения проводят в два этапа.
Этап 1. К балке через рычаг прикладывают нагрузку ступенями по 250 Н. Первой ступенью нагрузки является сам рычаг,от веса которого на балкудействует нагрузка 250 Н. Нагрузку прикладывают плавно без рывков. Перед тем как начать загружение балки, устанавливают индикатор к балке, а стрелку индикатора совмещают с нулевым делением шкалы. Перед загружением каждого этапа показание индикатора заносят в графу 3 табл. 1.
|
|
На каждом этапе загружения получают упругие деформации fупр и оста-точные деформации focm, которые заносят соответственно в графы 6 и 7 табл. 1. Полные деформации f = fупр + focm заносят в графу 8 табл.1. После приложения расчетной нагрузки Р определяют сумму деформаций упругих, остаточных и полных. В результате снятия нагрузки и подъема рычага, снимают отсчет по индикатору в течение 2-3 сек. Затем выдержка (в это время снимают грузы с рычага) до полного затухания деформаций (до 3-х минут) и берут отсчет, который должен быть близким к отсчету до загружения балки. Таким образом испытывают четыре типа балок.
Таблица 1
Сравнительная таблица работы цельного и составного сечения
| Величина | |||||||||||||
| Ступени загружения | Величина ступени загружения | Величина | прогиба, оп- | ||||||||||
| Показания индикатора, в мм | прогиба fупр, | ределенная | |||||||||||
| мм | теоретически, | ||||||||||||
| в мм f | |||||||||||||
| после начала | после выдержки | ||||||||||||
| до начала | загружения | на данной сту- | |||||||||||
| ступени | пени загружения | ||||||||||||
| ступени | fупр | focm | fполн | ||||||||||
| через 2-3 | в течение 3-5 | ||||||||||||
| загружения | |||||||||||||
| секунды | мин до прекра- | ||||||||||||
| щения роста | |||||||||||||
Этап 2. На рычаг навешивают грузы до расчетного значения силы Р (с учетом веса рычага). Стрелку индикатора выводят на нулевое положение. Затем плавно опускают рычаг с полным грузом Р на балку и снимают отсчет в течение 2-3 секунд. Результаты фиксируют в табл. 1 (fупр). Эту нагрузку выдерживают до полного прекращения роста прогиба и снова снимают показание индикатора (f = fупр + focm). Затем поднимают рычаг с грузом (балка разгружена) и в течение 2-3 секунд снимают отсчет, который фиксируют в табл. 1.После прекращения измерения прогиба (выдержка до 3-х минут) снимают последний отсчет и заносят в табл.1. Этап 2 выполняется только для балки типа (г).
5.Обработка результатов эксперимента
1.Определение величины расчетной нагрузки, приложенной в середине пролета балки.
Для балки (рис. 4) изгибающий момент определяют по формулам:
;
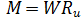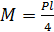; (3)
Откуда Р = 4∙ М / l, где Rи -расчетное сопротивление древесины изгибу (СНиП 11-25-80); l - пролет балки; W - момент сопротивления балки типа: а - W0= bh 2/3; б – Wn = KW ∙ Wч; в, г - Wч =2 bh 2/3 (KW - коэффициент податливости связей).
2. Определение максимального прогиба по схеме рис. 4.
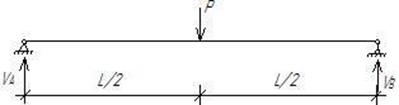
Рис. 4. Расчетная схема механических испытаний балок при статическом изгибе
Прогиб в однопролетной балке под действием сосредоточенной на-грузки Р определяется по формуле:
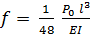, (4)
где I - момент инерции сечения; Е - модуль упругости материала балки (сосна); Р0- величина ступени нагружения, принимаемая в эксперименте 250 Н. Для балки типа «а»: Ia = hh 3/6; типа «б»: Iб=Iч ∙ kж; типа «в», «г»:
Iч = 2 bh 3/3
(kж -коэффициент,учитывающий понижение жесткости).
Прогибы определяются отдельно для каждого типа балок.
По данным прогибов этапа 1 строится график (рис.5 а). На данном графике показывают теоретическую прямую (пунктирная линия). Подоб-ные графики строят для всех четырех типов балок. По результатам этапа 2 строят график (рис.5, б), на котором прогиб с индексом «Н» означает про-гиб при нагрузке, а с индексом «Р» - при разгрузке.
| а) | б) | ||
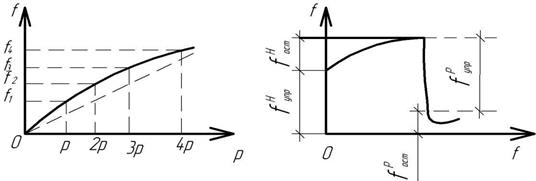
Рис.5. Графики прогибов: а – для 1 этапа; б – для 2 этапа
Полученные результаты эксперимента сравнивают с теоретическими и дается анализ расхождения.
Вопросы для самоконтроля
1. Как работают и рассчитываются брусчатые балки при изгибе?
2. В чем отличие составного элемента со связями на клею от элемента цельного такого же сечения?
3. Как рассчитывается изгибаемый элемент по прочности и по прогибам?
Лабораторная работа № 5