Значения для простого вещества 
| Tr | Pr | ||||||
| 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | 0,600 | 0,800 | |
| 0,30 | 16,782 | 16,774 | 16,764 | 16,744 | 16,705 | 16,665 | 16,626 |
| 0,35 | 15,413 | 15,408 | 15,401 | 15,387 | 15,359 | 15,333 | 15,305 |
| 0,40 | 13,990 | 13,986 | 13,981 | 13,972 | 13,953 | 13,934 | 13,915 |
| 0,45 | 12,564 | 12,561 | 12,558 | 12,551 | 12,537 | 12,523 | 12,509 |
| 0,50 | 11,202 | 11,200 | 11,197 | 11,192 | 11,182 | 11,172 | 11,162 |
| 0,55 | 0,115 | 9,948 | 9,946 | 9,942 | 9,935 | 9,928 | 9,921 |
| 0,60 | 0,078 | 8,828 | 8,826 | 8,823 | 8,817 | 8,811 | 8,806 |
| 0,65 | 0,055 | 0,309 | 7,832 | 7,829 | 7,824 | 7,819 | 7,815 |
| 0,70 | 0,040 | 0,216 | 0,491 | 6,951 | 6,945 | 6,941 | 6,937 |
| 0,75 | 0,029 | 0,156 | 0,340 | 6,173 | 6,167 | 6,162 | 6,158 |
| 0,80 | 0,022 | 0,116 | 0,246 | 0,578 | 5,475 | 5,468 | 5,462 |
| 0,85 | 0,017 | 0,088 | 0,183 | 0,408 | 4,853 | 4,841 | 4,832 |
| 0,90 | 0,013 | 0,068 | 0,140 | 0,301 | 0,744 | 4,269 | 4,249 |
| 0,93 | 0,011 | 0,058 | 0,120 | 0,254 | 0,593 | 1,219 | 3,914 |
| 0,95 | 0,010 | 0,053 | 0,109 | 0,228 | 0,517 | 0,961 | 3,697 |
| 0,97 | 0,010 | 0,048 | 0,099 | 0,206 | 0,456 | 0,797 | 1,570 |
| 0,98 | 0,009 | 0,046 | 0,094 | 0,196 | 0,429 | 0,734 | 1,270 |
| 0,99 | 0,009 | 0,044 | 0,090 | 0,186 | 0,405 | 0,680 | 1,098 |
| 1,00 | 0,008 | 0,042 | 0,086 | 0,177 | 0,382 | 0,632 | 0,977 |
| 1,01 | 0,008 | 0,040 | 0,082 | 0,169 | 0,361 | 0,590 | 0,883 |
| 1,02 | 0,008 | 0,039 | 0,078 | 0,161 | 0,342 | 0,552 | 0,807 |
| 1,05 | 0,007 | 0,034 | 0,069 | 0,140 | 0,292 | 0,460 | 0,642 |
| 1,10 | 0,005 | 0,028 | 0,055 | 0,112 | 0,229 | 0,350 | 0,470 |
| 1,15 | 0,005 | 0,023 | 0,045 | 0,091 | 0,183 | 0,275 | 0,361 |
| 1,20 | 0,004 | 0,019 | 0,037 | 0,075 | 0,149 | 0,220 | 0,286 |
| 1,30 | 0,003 | 0,013 | 0,026 | 0,052 | 0,102 | 0,148 | 0,190 |
| 1,40 | 0,002 | 0,010 | 0,019 | 0,037 | 0,072 | 0,104 | 0,133 |
| 1,50 | 0,001 | 0,007 | 0,014 | 0,027 | 0,053 | 0,076 | 0,097 |
| 1,60 | 0,001 | 0,005 | 0,011 | 0,021 | 0,040 | 0,057 | 0,073 |
| 1,70 | 0,001 | 0,004 | 0,008 | 0,016 | 0,031 | 0,044 | 0,056 |
| 1,80 | 0,001 | 0,003 | 0,006 | 0,013 | 0,024 | 0,035 | 0,044 |
| 1,90 | 0,001 | 0,003 | 0,005 | 0,010 | 0,019 | 0,028 | 0,036 |
| 2,00 | 0,000 | 0,002 | 0,004 | 0,008 | 0,016 | 0,023 | 0,029 |
| 2,20 | 0,000 | 0,001 | 0,003 | 0,006 | 0,011 | 0,016 | 0,021 |
| 2,40 | 0,000 | 0,001 | 0,002 | 0,004 | 0,008 | 0,012 | 0,015 |
| 2,60 | 0,000 | 0,001 | 0,002 | 0,003 | 0,006 | 0,009 | 0,012 |
| 2,80 | 0,000 | 0,001 | 0,001 | 0,003 | 0,005 | 0,008 | 0,010 |
| 3,00 | 0,000 | 0,001 | 0,001 | 0,002 | 0,004 | 0,006 | 0,008 |
| 3,50 | 0,000 | 0,000 | 0,001 | 0,001 | 0,003 | 0,004 | 0,006 |
| 4,00 | 0,000 | 0,000 | 0,001 | 0,001 | 0,002 | 0,003 | 0,005 |
Таблица 2.8
Состояния Ли-Кеслера
| Pr | |||||||
| 1,000 | 1,200 | 1,500 | 2,000 | 3,000 | 5,000 | 7,000 | 10,000 |
| 16,586 | 16,547 | 16,488 | 16,390 | 16,195 | 15,837 | 15,468 | 14,925 |
| 15,278 | 15,251 | 15,211 | 15,144 | 15,011 | 14,751 | 14,496 | 14,153 |
| 13,896 | 13,877 | 13,849 | 13,803 | 13,714 | 13,541 | 13,376 | 13,144 |
| 12,496 | 12,482 | 12,462 | 12,430 | 12,367 | 12,248 | 12,145 | 11,999 |
| 11,153 | 11,143 | 11,129 | 11,107 | 11,063 | 10,985 | 10,920 | 10,836 |
| 9,914 | 9,907 | 9,897 | 9,882 | 9,853 | 9,806 | 9,769 | 9,732 |
| 8,799 | 8,794 | 8,787 | 8,777 | 8,760 | 8,736 | 8,723 | 8,720 |
| 7,810 | 7,807 | 7,801 | 7,794 | 7,784 | 7,779 | 7,785 | 7,811 |
| 6,933 | 6,930 | 6,926 | 6,922 | 6,919 | 6,929 | 6,952 | 7,002 |
| 6,155 | 6,152 | 6,149 | 6,147 | 6,149 | 6,174 | 6,213 | 6,285 |
| 5,458 | 5,455 | 5,453 | 5,452 | 5,461 | 5,501 | 5,555 | 5,648 |
| 4,826 | 4,822 | 4,820 | 4,822 | 4,839 | 4,898 | 4,969 | 5,082 |
| 4,238 | 4,232 | 4,230 | 4,236 | 4,267 | 4,351 | 4,442 | 4,578 |
| 3,894 | 3,885 | 3,884 | 3,896 | 3,941 | 4,046 | 4,151 | 4,300 |
| 3,658 | 3,647 | 3,648 | 3,669 | 3,728 | 3,851 | 3,966 | 4,125 |
| 3,406 | 3,391 | 3,401 | 3,437 | 3,517 | 3,661 | 3,788 | 3,957 |
| 3,264 | 3,247 | 3,268 | 3,318 | 3,412 | 3,569 | 3,701 | 3,875 |
| 3,093 | 3,082 | 3,126 | 3,195 | 3,306 | 3,477 | 3,616 | 3,796 |
| 2,399 | 2,868 | 2,967 | 3,067 | 3,200 | 3,387 | 3,532 | 3,717 |
| 1,306 | 2,513 | 2,784 | 2,933 | 3,094 | 3,297 | 3,450 | 3,640 |
| 1,113 | 1,655 | 2,557 | 2,790 | 2,986 | 3,209 | 3,369 | 3,565 |
| 0,820 | 0,831 | 1,443 | 2,283 | 2,655 | 2,949 | 3,134 | 3,348 |
| 0,577 | 0,640 | 0,618 | 1,241 | 2,067 | 2,534 | 2,767 | 3,013 |
| 0,437 | 0,489 | 0,502 | 0,654 | 1,471 | 2,138 | 2,428 | 2,708 |
| 0,343 | 0,385 | 0,412 | 0,447 | 0,991 | 1,767 | 2,115 | 2,430 |
| 0,226 | 0,254 | 0,282 | 0,300 | 0,481 | 1,147 | 1,569 | 1,944 |
| 0,158 | 0,178 | 0,200 | 0,220 | 0,290 | 0,730 | 1,138 | 1,544 |
| 0,115 | 0,130 | 0,147 | 0,166 | 0,206 | 0,479 | 0,823 | 1,222 |
| 0,086 | 0,098 | 0,112 | 0,129 | 0,159 | 0,334 | 0,604 | 0,969 |
| 0,067 | 0,076 | 0,087 | 0,102 | 0,127 | 0,248 | 0,456 | 0,775 |
| 0,053 | 0,060 | 0,070 | 0,083 | 0,105 | 0,195 | 0,355 | 0,628 |
| 0,043 | 0,049 | 0,057 | 0,069 | 0,089 | 0,160 | 0,286 | 0,518 |
| 0,035 | 0,040 | 0,048 | 0,058 | 0,077 | 0,136 | 0,238 | 0,434 |
| 0,025 | 0,029 | 0,035 | 0,043 | 0,060 | 0,105 | 0,178 | 0,322 |
| 0,019 | 0,022 | 0,027 | 0,034 | 0,048 | 0,086 | 0,143 | 0,254 |
| 0,015 | 0,018 | 0,021 | 0,028 | 0,041 | 0,074 | 0,120 | 0,210 |
| 0,012 | 0,014 | 0,018 | 0,023 | 0,035 | 0,065 | 0,104 | 0,180 |
| 0,010 | 0,012 | 0,015 | 0,020 | 0,031 | 0,058 | 0,093 | 0,158 |
| 0,007 | 0,009 | 0,011 | 0,015 | 0,024 | 0,046 | 0,073 | 0,122 |
| 0,006 | 0,007 | 0,009 | 0,012 | 0,020 | 0,038 | 0,060 | 0,100 |
Одной из статистических поправок, которые необходимо учитывать при расчете энтропии вещества методом Бенсона, является поправка к вращательной энтропии на симметрию молекул. При этом полное число симметрии молекулы  (total - общий) разбивают на два слагаемых:
(total - общий) разбивают на два слагаемых:
на число симметрии наружного вращения молекулы в целом -  (наружное - external) и
(наружное - external) и
число симметрии вращающейся части молекулы или число симметрии внутреннего вращения 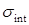 (внутреннее - internal). Полное число симметрии (
(внутреннее - internal). Полное число симметрии ( ) является произведением всех чисел симметрии молекулы:
) является произведением всех чисел симметрии молекулы:
 . (2.7)
. (2.7)
Число симметрии наружного вращения можно определить как число положений, которые может занимать жесткая многоатомная молекула (“жесткий ротатор”), совпадая при вращении со своей первоначальной конфигурацией.
Например, в двухатомных молекулах, состоящих из двух одинаковых атомов, последние могут поменяться местами при повороте молекулы на 180 градусов. Число симметрии наружного вращения таких молекул равно 2. Молекула CH4 представляет собой тетраэдр с атомами водорода в вершинах. Простым вращением молекулы вокруг каждой из связей “углерод-водород” можно получить 12 идентичных конфигураций, т.е. число симметрии наружного вращения молекулы метана равно 12.
Простой способ расчета числа симметрии для наружного вращения молекулы состоит в перемножении чисел, определяющих степень симметрии всех независимых осей, на количество этих осей. Так, для рассмотренной молекулы метана имеем четыре независимые оси третьего порядка, каждая из которых совпадает со связью С–Н. Вокруг этих осей происходит вращение молекулы. Таким образом, число симметрии наружного вращения молекулы метана равно 12 ( = 4·3 = 12). Молекула бензола имеет шесть осей второго порядка: три из них проходят через углеродные атомы, расположенные напротив друг друга
= 4·3 = 12). Молекула бензола имеет шесть осей второго порядка: три из них проходят через углеродные атомы, расположенные напротив друг друга

а три делят пополам углерод-углеродные связи. Все оси симметрии проходят через центр симметрии молекулы бензола. Таким образом, число симметрии наружного вращения молекулы бензола равно 12 ( = 6·2 = 12).
= 6·2 = 12).
Если часть молекулы способна вращаться относительно остальной ее части, то симметрия вращающейся части вносит дополнительные нефиксированные положения. Это приводит к необходимости введения второго числа симметрии -  .
.
Так, полное число симметрии молекул нормальных алканов равно 18 ( = = 2·9 = 18), где 2 - число симметрии наружного вращения молекулы по оси второго порядка, перпендикулярной основной цепи углерод-углеродных связей, а 9 - произведение чисел симметрии двух концевых метильных групп, каждая из которых имеет ось вращения третьего порядка.
= = 2·9 = 18), где 2 - число симметрии наружного вращения молекулы по оси второго порядка, перпендикулярной основной цепи углерод-углеродных связей, а 9 - произведение чисел симметрии двух концевых метильных групп, каждая из которых имеет ось вращения третьего порядка.
Для молекул разветвленных углеводородов с количеством метильных групп, равным “ n ”, число симметрии внутреннего вращения составляет  , а общее число симметрии будет равно
, а общее число симметрии будет равно  и может принимать весьма большие значения. Например, для неопентана (2,2-диметилпропана)
и может принимать весьма большие значения. Например, для неопентана (2,2-диметилпропана)  где 12 - число симметрии наружного вращения молекулы, 3 - ось симметрии третьего порядка в метильных группах, 4 - количество метильных групп в молекуле.
где 12 - число симметрии наружного вращения молекулы, 3 - ось симметрии третьего порядка в метильных группах, 4 - количество метильных групп в молекуле.
При расчете энтропии органических соединений других классов необходимо учитывать возможность заторможенного вращения прочих структурных фрагментов. Например, в молекулах ароматических углеводородов ось симметрии второго порядка имеют незамещенный фенил (C6H5 -) и пара-фенилен (-С6H4-).
Дать графическую зависимость изотерм и выполнить их анализ. Указать фазовые состояния окиси этилена при рассматриваемых параметрах. Критические температура, давление и ацентрический фактор окиси этилена соответственно равны 469 К, 71 атм и 0,200.
Решение
1. Рассчитываются  при интересующих температурах. Поскольку последние попадают в интервал, рассмотренный в примере 2.4, и на каждом из участков возможна линейная интерполяция теплоемкостей окиси этилена, то корректной будет и линейная интерполяция вычисленных в примере 2.4 значений
при интересующих температурах. Поскольку последние попадают в интервал, рассмотренный в примере 2.4, и на каждом из участков возможна линейная интерполяция теплоемкостей окиси этилена, то корректной будет и линейная интерполяция вычисленных в примере 2.4 значений  . Таким образом, имеем
. Таким образом, имеем
 = (288,86 – 274,12)/100×62,8+274,12 = 283,38 Дж/(моль×К).
= (288,86 – 274,12)/100×62,8+274,12 = 283,38 Дж/(моль×К).
Аналогично при температурах 304,85, 422,10 и 492,45 К имеем соответственно 243,52, 262,13 и 272,96 Дж/(моль×К).
2. Рассчитываются приведенные температуры:
 = 304,85/469 = 0,65;
= 304,85/469 = 0,65;  = 422,10/469 =0,90;
= 422,10/469 =0,90; 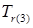 = 492,45/469 =1,05;
= 492,45/469 =1,05;  = 562,80/469 = 1,20.
= 562,80/469 = 1,20.
3. При полученных приведенных температурах и значениях приведенных давлений вычисляются значения 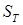 c помощью таблиц Ли-Кеслера и рассчитанных величин
c помощью таблиц Ли-Кеслера и рассчитанных величин  .
.
Для  и
и  = 3,55 атм имеем
= 3,55 атм имеем
 = 243,52 – (– ln (1/3,55)+(0,122+0,2×0,309))×8,31441 = 231,5 Дж/(моль×К).
= 243,52 – (– ln (1/3,55)+(0,122+0,2×0,309))×8,31441 = 231,5 Дж/(моль×К).
Фрагмент результатов расчета приведен в табл. 2.9 и 2.10, где жирным шрифтом выделены сведения, относящиеся к жидкому состоянию окиси этилена.

Рис. 2.2. Зависимость энтропии окиси этилена от давления
4. Зависимость  от давления при избранных температурах приведена на рис. 2.2. Характер полученных графических зависимостей различен для изотерм, принадлежащих жидкому и газообразному состояниям вещества. Энтропия жидкости в меньшей степени зависит от давления, чем энтропия газа, что очевидно. Для докритической изотермы резкое изменение энтропии сопряжено с изменением фазового состояния вещества.
от давления при избранных температурах приведена на рис. 2.2. Характер полученных графических зависимостей различен для изотерм, принадлежащих жидкому и газообразному состояниям вещества. Энтропия жидкости в меньшей степени зависит от давления, чем энтропия газа, что очевидно. Для докритической изотермы резкое изменение энтропии сопряжено с изменением фазового состояния вещества.
Таблица 2.9

|  при приведенном давлении,
при приведенном давлении, 
|  при приведенном давлении,
при приведенном давлении, 
| ||||||||
| 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | |
| 0,65 | 0,023 | 0,122 | 7,052 | 6,368 | 5,694 | 0,055 | 0,309 | 7,832 | 7,829 | 7,824 |
| 0,90 | 0,009 | 0,046 | 0,094 | 0,199 | 0,463 | 0,013 | 0,068 | 0,14 | 0,301 | 0,744 |
| 1,05 | 0,006 | 0,030 | 0,060 | 0,124 | 0,267 | 0,007 | 0,034 | 0,069 | 0,140 | 0,292 |
| 1,20 | 0,004 | 0,021 | 0,042 | 0,085 | 0,177 | 0,004 | 0,019 | 0,037 | 0,075 | 0,149 |
Таблица 2.10
 , Дж/(моль×К), при давлении, атм , Дж/(моль×К), при давлении, атм
| |||||||||||||
| T, K | 0,71 | 3,55 | 7,1 | 14,2 | 28,4 | 42,6 | 56,8 | 85,2 | 106,5 | ||||
| 304,85 | 246,1 | 231,5 | 155,6 | 155,5 | 155,3 | 155,2 | 155,1 | 154,9 | 154,8 | 154,6 | |||
| 422,10 | 264,9 | 251,1 | 244,8 | 237,9 | 229,2 | 189,4 | 188,9 | 188,6 | 188,2 | 187,7 | |||
| 492,45 | 275,7 | 262,1 | 256,0 | 249,6 | 242,4 | 237,3 | 232,8 | 228,1 | 222,0 | 212,4 | |||
| 562,80 | 286,2 | 272,6 | 266,7 | 260,5 | 253,8 | 249,5 | 246,1 | 243,1 | 240,4 | 236,5 | |||
Таким образом, при увеличении давления энтропия веществ, находящихся в газообразном состоянии, уменьшается, поскольку возрастает упорядоченность системы.