В общем случаецентральную статистику j(x, а), закон которой известен и не зависит от параметра, можно построить, основываясь на следующей лемме.
Лемма. Пусть x — непрерывная случайная величина с функцией распределения F (x). Тогда случайная величина
h = F (x) ~ R[0,1].
Действительно, определив функцию распределения Fh (y) случайной величины h:
Fh (y) = P {h º F (x) < y } =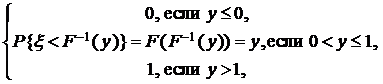 
убеждаемся, что это так.
Пусть при построении доверительного интервала мы используем некоторую статистику z(x1, x2…xn). Определим функцию распределения F (z, a)статистики z (F зависит от а).
z ~ F (z, a)
случайная величина j = F (z, a), если а есть истинное значение параметра, в силу леммы, распределена равномерно на отрезке [0, 1] при любом истинном значении а, и потому мы можем ее принять в качестве центральной статистики j(x, а) = F (z, a). в качестве (9) имеем соотношение (рис.9):
P {a <j = F (z, a) <1-a} = 1 - 2aº PД,
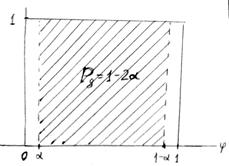справедливое при любом значении параметра а. Разрешив два неравенства под знаком вероятности относительно а, получим доверительный интервал.
Такой подход с некоторыми изменениями можно применить и для дискретных распределений.
Рис. 9. Выбор интервала для F (z, a)
Замечание 1. Можно рассуждать иначе. При любом фиксированном значении истинного параметра а определим интервал (z 1(a), z 2(a)) так, чтобы
P{ z1 (a)< z< z2 (a)} = РД. (15)
Ясно, что в качестве z1 и z2 можно взять квантили, т.е. определить z1 и z2 из условий
F (z 1, a) = (1 - РД) / 2, F (z 2, a) = (1 + РД) / 2.
Если z1 (a) и z2 (a) монотонно возрастают по а, то, разрешив два неравенства под знаком Р в (15) и учитывая, что z 1(a) < z 2(a),получим соотношение
P { z 2-1(z) < a < z1-1(z) } = РД,
верное при любом а. Я сно, что интервал (z2-1 (z), z1-1 (z)), определяемый двумя функциями от z, является доверительным с уровнем доверия Р Д..
Если z1 (a) и z2 (a) монотонно убывают по а, то доверительный интервал получим таким же образом.
При построении односторонних границ нужно вместо двух неравенств использовать лишь одно, согласовав знак неравенства с типом границы (верхняя или нижняя) и с характером монотонности (убывание или возрастание).
Пример 1. Пусть x1, x2…x n — независимые наблюдения над нормальной N (m, s2) случайной величиной. Пусть дисперсия s2 известна. Построим доверительный интервал для среднего m с уровнем доверия Р Д = 1 – 2a. Оценкой для m является статистика`x =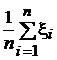 
, имеющая функцию распределения 
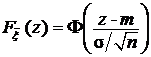, где Ф(x) - функция стандартного нормального распределения. Согласно лемме, случайная величина 
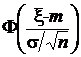распределена равномерно на отрезке [0,1], следовательно,
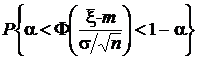= 1 – 2a = P Д
при любом истинном значении m. После разрешения двух неравенств под знаком вероятности получим
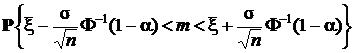= P Д,
где учтено, что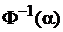 
= - 
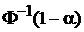. Обозначив 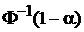= fP, получаем интервал (
, 
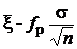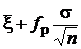), совпадающий с (8).
Пример 2. Пусть x1, x2…x n — независимые наблюдения над случайной величиной, распределенной равномерно на отрезке [0, a ], где a — неизвестный параметр, для которого нужно построить верхнюю доверительную границу с доверительной вероятностью P Д = 1 – a. Оценивающей статистикой является z =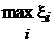 
— достаточная для а статистика. определим функцию распределения случайной величины z:
F z(z, a) =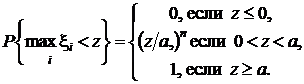 
Случайная величина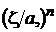 
распределена равномерно на [0,1], и потому при любом а
,
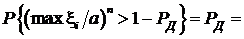
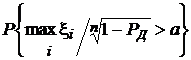что означает, что статистика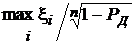 
является верхней доверительной границей для а с коэффициентом доверия P Д.
Верно также при любом а
,
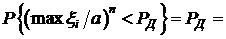
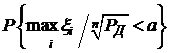т.е. статистика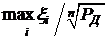 
является нижней доверительной границей.
Замечание 2. Общая логика построения доверительного множества по статистике z заключается в следующем. Для каждого значения параметра а построим множество Z(a) значений z случайной величины z вероятности РД; конечно, оно зависит от а, Z= Z(a):
P{z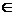 
Z(a)}= Р Д 
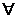a.
Далее для любого z построим множество A(z) значений параметра а, включив в него те значения а, для которых Z(a) содержит z:
A(z) = { a: z 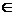Z(a)}, т.е. a 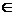A(z) 
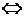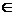z Z(a),
и потому случайное множество A(z) содержит истинное значение а с вероятностью
P{A(z) ' a } = P{z 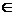Z(a)} = Р Д 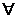a.