Использование асимптотической нормальности оценок.
Пусть по выборке x = (ξ1, ξ2…ξ n) оценивается неизвестный параметр а, и пусть оценка â = â (x) асимптотически нормальна со средним а и дисперсией 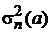 , зависящей от неизвестного параметр а. Рассмотрим нормированную погрешность
, зависящей от неизвестного параметр а. Рассмотрим нормированную погрешность
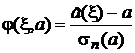 . (16)
. (16)
Эта случайная величина распределена приближенно по нормальному закону N (0,1) при любом значении параметра а. По заданному значению доверительной вероятности PД определяем симметричный интервал(- f P, f P), который несет в себе вероятность PД нормального N (0,1) распределения, и потому при любом значении параметра а верно приближенное соотношение:
P {çj(x, a)ç < f P}» PД, 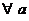 .
.
Полагая монотонность j по a и разрешая под знаком вероятности неравенства
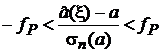 , (16а)
, (16а)
относительно а, получим соотношение
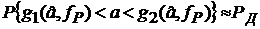 ,
,
верное при любом значении параметра а. Это означает, что 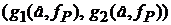 является доверительным интервалом для параметра а с коэффициентом доверия, приближенно равным PД.
является доверительным интервалом для параметра а с коэффициентом доверия, приближенно равным PД.
Замечание. Сказанное можно обобщить. Вместо оценки 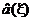 рассматрим z = z(ξ1, ξ2…ξ n) – некоторую статистику, распределенную приближенно нормально с мат. ожиданием m (a) =Mz и дисперсией s2 (a) =Dz. Пронормировав z, вместо (16), получаем с.в.:
рассматрим z = z(ξ1, ξ2…ξ n) – некоторую статистику, распределенную приближенно нормально с мат. ожиданием m (a) =Mz и дисперсией s2 (a) =Dz. Пронормировав z, вместо (16), получаем с.в.:
j(z, а)= 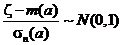
Все остальное будет справедливым, в результате получим доверительный интервал.
Примеры
А. доверительный интервал для вероятности. Пусть Р (А) = а — неизвестная вероятность некоторого события А, и x — число появлений А в серии n независимых испытаний. Несмещенной оценкой для а является 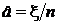 , которая по теореме Муавра-Лапласа при больших значениях числа испытаний n является асимптотически нормальной с параметрами
, которая по теореме Муавра-Лапласа при больших значениях числа испытаний n является асимптотически нормальной с параметрами
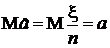 ,
, 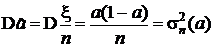 ,
,
и потому нормированная погрешность
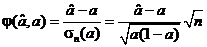
распределена приближенно по нормальному закону N (0,1) при любом значении параметра а. Разрешая неравенство (16)
|
|
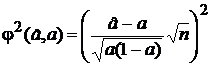 < f P2
< f P2
относительно а, получаем доверительный интервал 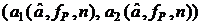 , где а 1, а 2 — корни соответствующего квадратного уравнения
, где а 1, а 2 — корни соответствующего квадратного уравнения
а 1,2 = 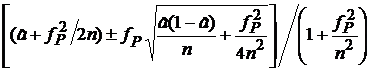 .
.
При больших n формула упрощается:
а 1,2 » 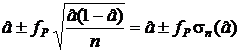 .
.
При малых значениях n, когда нельзя пользоваться приближенной нормальностью, пользуются статистическими таблицами, в которых для заданных n и P Д и полученному значению оценки â указаны левый и правый концы интервала. Вставить номограмму
Б.Доверительный интервал для коэффициента корреляции. Пусть имеется пара случайных величин (x, h), для которых по имеющейся выборке (x1, h1), (x2, h2)…(x n, h n) нужно определить доверительный интервал для коэффициента корреляции
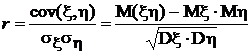 .
.
напомним практический смысл: прогноз: 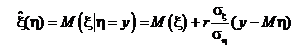
Методом моментов получаем оценку для r: 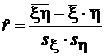 ,
,
где обозначено
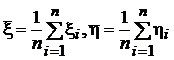 ,
, 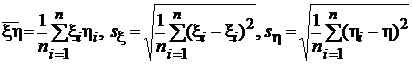 .
.
Если распределение случайных величин (x, h) является нормальным, оценка 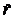 распределена при больших n приближенно нормально [4], причем
распределена при больших n приближенно нормально [4], причем
М 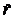 = r, D
= r, D 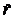 =
= 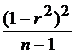 .
.
Этого достаточно, чтобы определить приближенный доверительный интервал. Однако, более удобным является другой способ, основанный на преобразовании z Фишера:
z = z (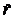 ) =
) = 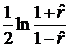 .
.
Эта статистика распределена приближенно (при n 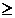 20) по нормальному закону [4] со средним
20) по нормальному закону [4] со средним
mz (r)» 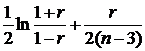
и дисперсией s2 » 1 / (n – 3), а статистика
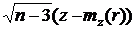 ~ N (0,1)
~ N (0,1)
приближенно нормальна. Доверительный интервал для r получаем из неравенства
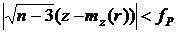 ,
,
где f P = Q((1 + P Д) / 2) — квантиль уровня (1 + P Д) / 2 нормального распределения. В статистических таблицах (например, [4]) даны интервалы для заданных n, P Д и 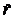 . Для примера укажем, что при P Д = 0,95 и
. Для примера укажем, что при P Д = 0,95 и 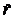 = 0,8 интервалы составляют:
= 0,8 интервалы составляют:
|
|
(0,32; 0,95) при n = 10 и (0,53; 0,92) при n = 20.