МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Лекция 6
Повтор.
Определение. Интервал I (x) = (a1 (x), a2 (x)) со случайными концами (случайный интервал), определяемый двумя функциями наблюдений, называется доверительным интервалом для параметра a с уровнем доверия Р Д (обычно близким к 1), если
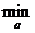P { I (x) ' a } º 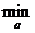P { a 1(x)< a < a 2(x)} = P Д, (1)
т.е. если при любом значении параметра a вероятность (зависящая от a) накрыть случайным интервалом I (x) истинное значение a велика, не менее заданной величины Р Д.
Один из способов был виден из примера: оценка среднего нормальной совокупности. Пусть x = (x1, ξ2 ... x n) N (a, σ2)совокупности, a=?, σ известно.
â = â (x1,ξ2…x n) =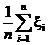 
º`x- оценивающая статистика, з.р. известен N (a, 
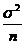) (3)
`x ºz - оценивающая статистика (можно взять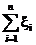 
-тоже оценивающая ст-ка)
1.Конструируем с.в. 
введением параметра a так, чтобы з.р. был известен: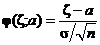 
, (4)
2. По заданному уровню доверия Р Д определим для j интервал (f 1, f2) так, чтобы он содержал в себе вероятность Р Д, т.е.
. 
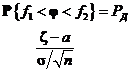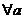(5)
3). Разрешаем неравенства под знаком вер-ти:
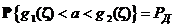(6)
Теперь под знаком вероятности стоит событие, состоящее в том, что случайный интервал накроет неизвестное значение параметра с заданной большой вероятностью Р Д при любом значении параметра, т.е.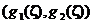 
- доверит. инт-л с уровнем доверия Р Д.
Конец повтора
Доверительные границы -2
Интервалы для параметров нормального распределения
А. Распределение хи-квадрат c k степенями свободы. Для рассмотрения типичных практических примеров потребуются сведения о некоторых распределениях. Многие задачи статистики связаны с распределением хи-квадрат (χ2(k)).
Пусть a1, a2…a k — независимые случайные величины, распределенные по стандартному нормальному закону N (0,1). Рассмотрим сумму их квадратов и обозначим соответствующую случайную величину через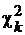 
:
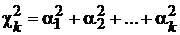. (10)
Распределение этой случайной величины называют
распределением хи-квадрат с k степенями свободы.
Нетрудно показать (см., например, [2], Гнеденко, Курс теории вероятностей, §24), что плотность этого распределения выражается следующей формулой:
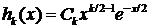, x > 0, (11)
где Сk =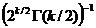 
— нормирующий множитель, 
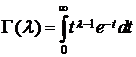— знаменитая гамма-функция; напомним, что 
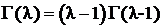, и при целом l, 
.
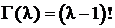На рис. 8 показаны графики при различных значениях k.
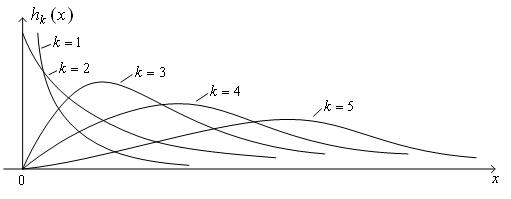
Рис. 8. Семейство плотностей распределения χ2
Заметим, что при k = 2 получаем показательное распределение:
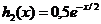~ Е (1/2).
Из соотношения (10) получаем первые два момента:
M 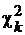= k, D 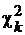= 2 k,
Проверяем: D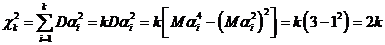 
Ясно, что с увеличением числа k степеней свободы распределение c2(k) смещается вправо и расплывается,
а также, что оно асимптотически нормально (в силу центральной предельной теоремы):
c2(k) ~ N (k, 2 k) при k ®¥;
при k > 30 можно пользоваться таблицами нормального распределения.
Далее отметим полезные сведения.
Замечание о связи с гамма-распределением. Распределение c2- хи-квадрат является частным случаем гамма-распределения, для которого плотность выражается формулой
p (x; l ,a) = C (l ,a)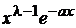 
, x >0, l > 0, a > 0 (двухпараметрическое),
где C (l ,a) =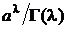 
- нормирующий множитель; l – параметр формы, a – параметр масштаба, 
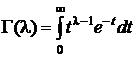- гамма-функция. Первые два момента m 1 и s2 равны соответственно
m 1 = l/ a, s2 = l/ a 2.
Характеристическая функция f(t) этого распределения выражается формулой:
f(t)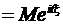 
= 
= 
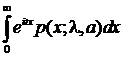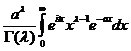
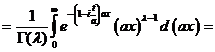
новая переменная интегрирования: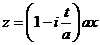 
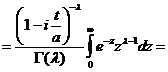
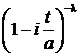. (12)
Если l — целое число, то распределение называется распределением Эрланга, которому подчиняется сумма l независимых случайных величин, показательно распределенных с плотностью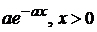 
.
Справедливость формулы (11) можно легко показать, определив характеристические функции для a12 и затем для 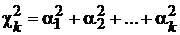. характеристическая функция для случайной величины 
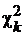оказывается равной
(1–2 it)- k /2,
откуда следует, что соответствующее распределение является гамма-распределением с параметрами l = k /2, a = 1/2.
Б. Совместное распределение выборочных среднего и дисперсии нормальной совокупности. (важный вопрос! обобщнеие в регрессионном анализе)
Теорема. Пусть x = (x1, x2…x n) — выборка N (m, s2),
оценки параметров:
`x=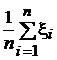 
— s 2 = 
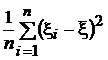выборочные среднее и дисперсия.
Утверждения:
1) эти статистики `x и s 2 независимы;
2) с. в.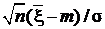 
~ N (0, 1)- стандартный нормальный закон,
3) n s2/s2 ~c2(n -1) — хи-квадрат с числом степеней свободы (n -1).
Доказательство. Перейдем нормировкой к новым случайным величинам
h i = (x i – m)/s, i = 1, 2… n, которые образуют выборку
h =(h1, h2…h n) из совокупности, распределенной по N (0, 1). Тогда
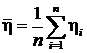= (`x– m)/s,
Далее:
= 
= 
= 
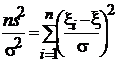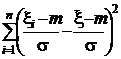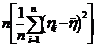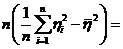
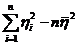; (13)
здесь предпоследняя сумма есть умноженная на n дисперсия выборочного распределения.
Преобразуем вектор h с помощью ортогонального преобразования с матрицей С:
z = Сh,
где первая строка матрицы С состоит из одинаковых элементов, равных 1 /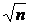 
. Дисперсионная матрица z, с учетом того, что
M(hhT) = I и С T= С -1,
равна
Dz= MСh(Сh)T = СM(hhT)С T = I,
где I — единичная матрица, и потому z1, z2…z n — независимые случайные величины, распределенные по N (0, 1).
Если учесть, что ортогональное преобразование не меняет расстояния, т. е.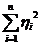 
= 
,
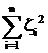а для первого элемента справедливо соотношение
z1 =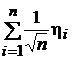 
= 
,
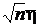то выражение (13) примет вид
= 
= 
.
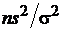
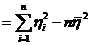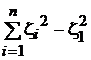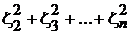Последняя сумма ns 2/s2 распределена по закону хи-квадрат с (n –1) степенями свободы и не зависит от
z1= =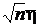 
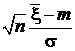, т.е. от`x.
Именно это утверждает данная теорема.
В. Доверительный интервал для дисперсии нормальной совокупности. Пусть x = (x1, x2…x n) — выборка из совокупности, распределенной по нормальному закону N (m, s2). Задан коэффициент доверия P Д.
Параметр m может быть известен или не известен, поэтому рассматриваем два случая одновременно. в качестве несмещенных оценок для s2 используем статистики:
если m известно, то
s 2 =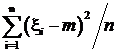 
, и тогда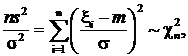 
иначе
s 2=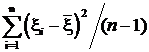 
, и тогда 
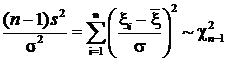по теореме.
Рассмотрим случайную величину
j(x, m, s) =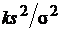 
, где k =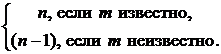 
Очевидно, что в обоих случаях случайная величина j подчиняется закону распределения хи-квадрат с k степенями свободы.
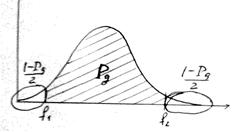
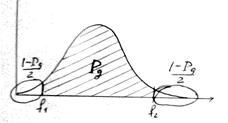
Определим интервал (f 1, f 2) так, чтобы
P { f 1 < j < f 2} = P Д.
В качестве f 1 и f 2 возьмем квантили уровней соответственно (1 – Р Д) / 2 и (1 + Р Д) / 2 распределения хи-квадрат с k степенями свободы:
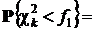(1- Р Д)/2, 
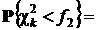(1+ Р Д)/2.
Разрешая под знаком вероятности два неравенства относительно s
f 1 < j = 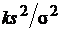< f 2,
получим соотношение
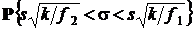= P Д
верное при любых значениях m иs, откуда следует, что интервал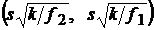 
является доверительным для s с доверительной вероятностью P Д.
Пример. Пусть среднее m неизвестно, n = 2, P Д = 0,95. Тогда
s =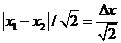 
,
и доверительный интервал весьма широк — (0,5 s, 30 s).
При n = 10: (0,7 s, 1,8 s),
при n = 20 — (0,87 s, 1,17 s).
Вывод: если оцениваете с.к.о., не верьте точечной оценке, обязательно считайте доверит. интервал.
Г. Распределение Стьюдента. Многие задачи статистики приводят к рассмотрению следующей случайной величины.
Пусть с.в.: a, N (0,1),
и с.в.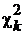 
, ~ хи-квадрат с k степенями свободы.
Образуем новую случайную величину Tk следующим образом:
Tk =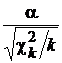 
. (14)
Распределение этой случайной величины называется распределением Стьюдента (псевдоним английского статистика В. Госсета) с k степенями свободы и обозначается s (k). Плотность sk (x) распределения выражается формулой:
sk (x) =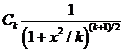 
, - ¥ < x < ¥,
где Ck =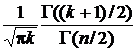 
— нормирующий множитель.
При k = 1 распределение Коши с плотностью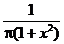 
.
При увеличении k знаменатель в (14) сходится к 1, поскольку математическое ожидание
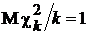, а дисперсия 
,
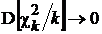и потому распределение S (k) сходится к стандартному нормальному.
При k > 30 для вероятностей p > 0,01 можно нормальным распределением.
Tk ~ N (0, 1);
Д. Доверительный интервал для среднего нормальной совокупности при неизвестной дисперсии.
Пусть x = (x1, x2…xn) — выборка из совокупности, распределенной по нормальному закону N (m, s2). Построим доверительный интервал с коэффициентом доверия P Д. параметр s неизвестен, но именно он определяет точность оценки, т.е. ширину интервала, поэтому его тоже нужно оценить.
Пусть`x= 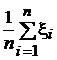— оценка м.о. ~ N (m, 
s2.)
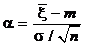~ N (0, 1) - стандартный нормальный закон,
s 2 =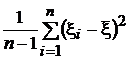 
— оценка дисперсии,
~ 
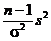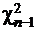- распределение хи-квадрат с (n –1) степенями свободы,
и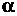 
и s 2 независимы.
Построим статистику Tn -1 делением
Tn -1 =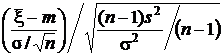 
= 
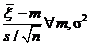=j
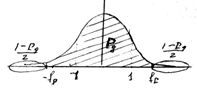Неизвестное значение s сократилось. в силу определения с.в. с законом Стьюдента и теоремы о независимости выборочных среднего и дисперсии нормальной совокупности, эта статистика подчиняется закону Стьюдента с (n– 1) степенями свободы. По заданному коэффициенту доверия P Д определяем симметричный интервал (- tP, tP) такой, что
P {- tP <Tn -1 < tP } = P Д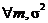 
Очевидно, что tP есть квантиль уровня (1+ P Д) / 2.
Разрешая под знаком вероятности два неравенства относительно параметра m
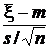- tP < 
< tP,
получаем:
P {`x - tP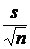 
< m <`x+ tP 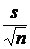} = P Д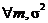
Последнее соотношение верно при любых значениях параметров m и s, и потому случайный интервал {`x - tP 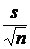,`x + tP 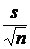} является доверительным с вероятностью P Д.
Замечание. Сравнение полученного интервала с интервалом,
(
, 
)
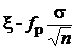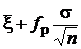построенным при известной дисперсии (первый пример построения интервала). Видно, что в полученном интервале вместо известного значения s фигурирует оценка s для s, и вместо квантили fP нормального распределения N (0,1) появилась квантиль tP распределения S (n- 1) Стьюдента. Отметим, что при равных доверительных вероятностях tP > fP. В табл. 2 для примера приведены некоторые значения.
Табл. 2. Сравнительные значения fP и tP
| P Д | fP | tP | |||
| n = 5 | n = 10 | n = 20 | n = 50 | ||
| 0.95 | 1.96 | 2.57 | 2.23 | 2.09 | 2.00 |
| 0.99 | 2.58 | 4.03 | 3.17 | 2.85 | 2.66 |