Методические указания к решению задач. Задачи № 1 – 7. Сила аутогезии между частицами муки, медианный диаметр которых

Задачи № 1 – 7. Сила аутогезии между частицами муки, медианный диаметр которых составляет 40 мкм, равна 5,5×10^-6Н. Рассчитать силу аутогезии слоя частиц муки в обычных условиях и после слёживания, если пористость (П) муки уменьшилась с 0,46 до 0,2, а сила аутогезии между отдельными частицами возросла в 5 раз. Определить, во сколько раз увеличилась сила аутогезии в результате слеживания.

1. Определяем площадь, приходящуюся на одну частицу

2. Число частиц на 1м² контакта слоя муки (без слёживания) с учетом пористости

3. Сила аутогезии слоя муки в расчете на 1м².

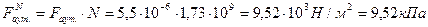
4. Число частиц на 1м² контакта слоя муки (после слёживания) с учетом пористости

5. Сила аутогезии слоя муки (с учетом пористости) после слеживания

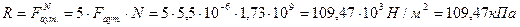
6. Сила аутогезии слоя муки увеличилась в результате слеживания в n раз.

раз.

Примечание:

Пористость - отношение объёма порового пространства между частицами к объёму сыпучей пищевой массы.

Например: пористость 0,33 означает, что 33% объема пищевой массы занимает поровое пространство, а 67% частицы.

Задачи №8 - 10. Когда движение сыпучей массы происходит по поверхности разнородных тел, т.е. осуществляется адгезионное движение, то согласно двучленному закону трения его можно представить следующим образом:

F^т_отр.= m×(F^N_ад. + Р_вд.),

где m – коэффициент внешнего трения.

Результаты измерений можно представить прямыми 3 и 3`, коэффициент внешнего трения равен тангенсу угла наклона этих прямых; т.е. tga = m.

Отрезок, отсекаемый на оси ординат, равен сцеплению при адгезии:

С_ад. = m × F^N_ад.

Рисунок 1 - Зависимость усилия сдвига F^т_отр. от нормального давления Р_в.д.:

1 - при отсутствии адгезии или аутогезии;

2,2` - аутогезионный отрыв (движение);

3,3`- адгезионный отрыв (движение).

Прямые 2 и 2` (рисунок 1) отражают аутогезионное движение сыпучей массы, которое аналитически определяется уравнением:

F^т_отр.= m_в×(F^N_аут. + Р_вд.)

Отрезок, отсекаемый на оси ординат, в этом случае, равен сцеплению при аутогезии:

С_аут. = m_в × F^N_аут.

Данные из условия задачи нужно представить, как показано на рисунке 1, т.е. нужно построить график и по тангенсу углов a определить коэффициенты внешнего трения и внутреннего трения сыпучей массы. Величины сцепления адгезионного и аутогезионного находят из графика по отрезкам, отсекаемым построенными прямыми на оси ординат.

Из формул С_ад. = m × F^N_ад., С_аут. = m_в × F^N_аут по найденным значениям коэффициентов трения m, m_в и сцеплений С_ад., С_аут. рассчитывают F^N_ад., а также F^N_аут., т.е. адгезию и аутогезию в расчете на 1 м² поверхности.

Задачи №11- 14. Решение

Задачи №15-21. При решении исходят из того, что пластическая прочность Р_с структурированных пищевых масс связана со средней силой сцепления 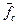соотношением:

Р_с ≈n ,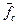

где

n=к/d² – среднее число контактов на единице поверхности сдвига;

d – диаметр частицы;

к – структурный параметр, определяется по таблице для заданного содержания дисперсной фазы.

Задачи №22 – 27. Зная правила последовательного и параллельного соединения элементарных моделей, нужно составить сложную модель из элементарных по значениям, представленным в таблицах в условии задачи. Элементарные модели схематично изображают квадратами.

Рисунок 2 - Последовательное (а) и параллельное соединение элементов (б) реологических моделей

При последовательном соединении элементарных моделей полная нагрузка Р приходится на каждый элемент, а полная деформация g или ее скорость складываются из дефор­маций и скоростей составляющих элементов:

Р = Р₁ = Р₂ =¼= Р_n

g = g₁ + g₂ +¼+ g_n и = ₁ + ₂ +¼+ _n

При параллельном соединении элементарных моделей деформации g и их скорости одинаковы для всех элементов, а полная нагрузка Р складывается из нагру зок отдельных элементов:

Р = Р₁ + Р₂ +... + Р_n

g = g₁ = g₂ =¼= g_n и = ₁ = ₂ =¼= _n

Задачи №28-30. Механическая модель Максвелла представляет последовательное соединение элемента жесткости и вязкости. Изменение напряжения сдвига во времени при постоянной деформации описывается следующим уравнением:

.

В логарифмических координатах это уравнение прямой линии:

lns_t = lns₀ – (1/λ)∙t.

Построив графическую зависимость lns_t от t, по тангенсу угла наклона прямой можно найти λ^-1, а затем и λ – время релаксации напряжения.