МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Рязанский государственный радиотехнический университет
Вечерний факультет
Контрольная работа
по дисциплине:
«Многомерные графы»
Выполнил: студент группы 3030 Лапин Алексей Алексеевич
Проверил:
Кабанов Анатолий Николаевич
г. Рязань 2015 г.
Лабораторная работа № 1
Упорядоченные множества элементов. Структура
И способы представления многомерных матриц
Теоретическая часть
Круг задач, которые представляются дискретными моделями, чрезвычайно широк и разнообразен: графы, транспортные потоки, логические системы, информацинно-поисковые системы, системы распознавания образов и многие другие. Особую трудность в решение дискретных задач вносит специфика многоуровневого управления, заключающаяся в том, что в дискретных моделях используются многоиндексные переменные. Например, множество А{i,j,k,l,m}, А - оценка, i - номер предмета, j - номер преподавателя, k - время, l - номер группы, m - номер студента удобно представлять с помощью многомерных матриц.
Многомерной матрицей (ММ) называется упорядоченная совокупность многоиндексных элементов ai1i2…iW, где ia=1,2,…,na; 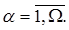 Целые положительные числа W, NA=n1n2…nW,na называются соответственно размерностью матрицы А, размером матрицы А, размером индекса ia. Размерность W показывает число индексов в обозначении элементов ai1i2…iW матрицы. Размер NA матрицы А указывает общее число элементов матрицы. Размер индекса na показывает, сколько значений (от 1 до na) пробегает соответствующий индекс.
Целые положительные числа W, NA=n1n2…nW,na называются соответственно размерностью матрицы А, размером матрицы А, размером индекса ia. Размерность W показывает число индексов в обозначении элементов ai1i2…iW матрицы. Размер NA матрицы А указывает общее число элементов матрицы. Размер индекса na показывает, сколько значений (от 1 до na) пробегает соответствующий индекс.
Структура многомерных матриц определяется структурой их индексов. Структура индекса может быть столбцовой или строчной. Индексы, имеющие, например, строчную структуру (строчные индексы), показывают положение элементов внутри какого-либо столбца. При индексном представлении элементов матрицы целесообразно ставить знак + или – соответственно над столбцовым или строчным индексом. Например,  - элементы обычной двухмерной (плоской) матрицы. Общее представление многомерной матрицы А имеет вид А = А(p,g), где р – число столбцовых индексов, g – число строчных индексов. Для получения индексного представления многомерной матрицы вводится помечивание индексов. Пометка начинается с последнего индекса, который при g>0 принимается за строчный. Далее столбцовые и строчные индексы чередуются до тех пор, пока один из видов индексов не исчерпывается. При p³g все оставшиеся индексы принимаются за столбцовые, при p<g – за строчные. Числа p и g в сумме дают размерность W матрицы А: p+g=W. Если матрица А является функциональной, например зависит от времени t, от пространственных координат x, y и т.д., то структурные числа p и g следует отделять от аргументов точкой с запятой, например A=A(p,g;t,x,y). Для наглядного представления многомерной матрицы используют табличное представление. Табличное представление многомерной матрицы – это блочно-иерархическая таблица, отображающая на плоскости структуру матрицы и численные значения элементов. Иерархия согласована с иерархией индексов таким образом, что крайним левым индексам соответствуют наиболее крупные блоки. При этом столбцовые индексы изменяются в столбцах, а строчные – в строках. Примеры представления многомерных матриц приведены в табл.1.1.
- элементы обычной двухмерной (плоской) матрицы. Общее представление многомерной матрицы А имеет вид А = А(p,g), где р – число столбцовых индексов, g – число строчных индексов. Для получения индексного представления многомерной матрицы вводится помечивание индексов. Пометка начинается с последнего индекса, который при g>0 принимается за строчный. Далее столбцовые и строчные индексы чередуются до тех пор, пока один из видов индексов не исчерпывается. При p³g все оставшиеся индексы принимаются за столбцовые, при p<g – за строчные. Числа p и g в сумме дают размерность W матрицы А: p+g=W. Если матрица А является функциональной, например зависит от времени t, от пространственных координат x, y и т.д., то структурные числа p и g следует отделять от аргументов точкой с запятой, например A=A(p,g;t,x,y). Для наглядного представления многомерной матрицы используют табличное представление. Табличное представление многомерной матрицы – это блочно-иерархическая таблица, отображающая на плоскости структуру матрицы и численные значения элементов. Иерархия согласована с иерархией индексов таким образом, что крайним левым индексам соответствуют наиболее крупные блоки. При этом столбцовые индексы изменяются в столбцах, а строчные – в строках. Примеры представления многомерных матриц приведены в табл.1.1.
Таблица 1.1
| Общее представление | Индексное представление | Табличное представление | ||||||||||||||||||
| А(0,1) | {  }
i = }
i = 
|
| ||||||||||||||||||
| А(1,2) | {  }
i,j,k = }
i,j,k = 
|
|
В некоторых частных, но важных случаях приходится пользоваться плоскими табличными представлениями многомерной матрицы, которые являются обычными плоскими матрицами и получаются из табличного представления путем снятия всех перегородок. Их обозначают следующим образом:  Атабл = {A(p,g)}табл.
Атабл = {A(p,g)}табл.
В ряде случаев записи математических выражений удобно представлять многомерные матрицы с помощью мультииндексов

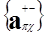 , (1.1)
, (1.1)
где p+ - столбцовый мультииндекс, имеющий вид столбца
p+ = [i1+, i2+,…,Ip+]T;
 - строчный мультииндекс, имеющий вид строки
- строчный мультииндекс, имеющий вид строки  =[j1-, j2-,…,jq-]T.
=[j1-, j2-,…,jq-]T.
Следует отметить, что обозначение мультииндексов в соотношении (1.1) является условным, так как индексы должны располагаться в соответствии с правилом помечивания, т.е. чередоваться, а не группироваться по столбцовому и строчному признакам, как это следовало бы из буквального понимания соотношения (1.1).
Основные операции над многомерными матрицами
Помечивание для индексного представления матриц:

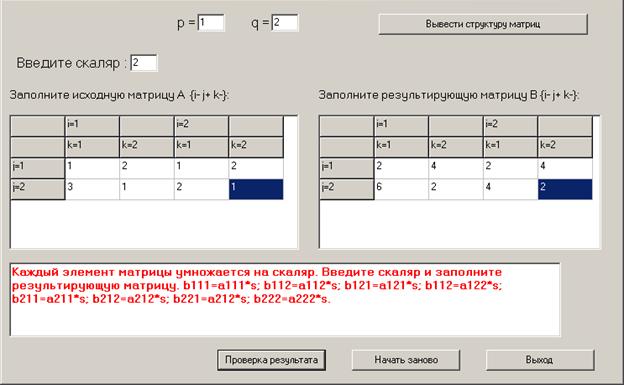
Умножение ММ на скаляр
Каждый элемент матрицы умножается на скаляр.
С помощью мультииндексов это можно представить в виде
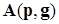 *
* 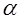 ={
={ 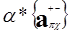 }.
}. 


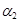
 111
111