Многомерная матрица В=А-1 называется обратной по отношению к гиперквадратной матрице А=(р,р), если выполняются следующие соотношения:
А(р,р)×В = В×А(р,р) = Е(р,р). (1.2)
Обратная многомерная матрица существует тогда и только тогда, когда определитель исходной гиперквадратной матрицы отличен от нуля. Численное обращение гиперквадратной матрицы может осуществляться путем плоского обращения ее двумерного табличного представления.
Псевдообратной многомерной матрицей В(g,p) = A+(g,p) по отношению к матрице А(р,g) называется матрица В, удовлетворяющая следующим аналогам условий Мура-Пенроуза:
a) A(p,g)B(g,p)A(p,g) = A(p,g);
б) B(g,p)A(p,g)B(g,p) = B(g,p);
в)[B(g,p)A(p,g)]T = B(g,p)A(p,g);
г) [A(p,g)B(g,p)]T = A(p,g)B(g,p).
Псевдообратная матрица всегда существует, и ее табличное представление совпадает с результатом псевдообращения двумерного табличного представления исходной матрицы. При этом выполняется условие – если обратная матрица существует, то она совпадает с псевдообратной: A+(p,g) = A-1(p,g).
Таким образом, общее правило получения обратной матрицы можно записать следующим образом.
1. Обратная матрица строится на основе обращения (псевдо-обращения) ее табличного представления.
2. Индексы обратной матрицы располагаются так же, как при транспонировании матрицы. Построенная таким образом матрица определяет структуру обратной матрицы, а значения ее элементов устанавливаются по табличному представлению обратной матрицы. Примечание. Многомерные обратные матрицы могут использоваться для представления решения линейных многомерно-матричных уравнений типа А(р,р)×Х(р,0)=В(р,0), которое дается соотношением: Х(р,0) =А-1(р,р)×В(р,0).
Результаты программного контроля выполнения работы
|
|
Лабораторная работа № 2
Экстремальный путь в графе.
Определение кратчайшего пути между двумя
Вершинами графа
Теоретическая часть
Рассмотрим алгоритм решения для случая многомерного графа. В конечном многомерном графе каждой дуге поставлено в соответствие число Сi1,i2,,,il,m1,m2,,ml, называемое длиной дуги из вершины xi1,i2,,il в вершину xm1,m2,,ml. Требуется найти путь наименьшей длины, ведущий из некоторой вершины S в некоторую вершину t. Для использования табличного представления многомерных матриц введем помечивание индексов Ci1 
,i1 
,,m1 ,ml . Алгоритм включает в себя 3 шага.
Предварительный шаг. В табличном представлении матрицы C столбец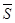 
помечивается знаком *. Диагональному элементу в столбце 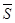, т.е. 
, придается значение 
. Помеченные вершины будем относить к множеству R, непомеченные – к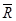 
, т.е. S Î R.
Общий шаг. Рассмотрим все дуги, исходящие из множества помеченных вершин R и заканчивающиеся на непомеченных вершинах 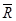. Для каждой дуги найдем
hm ,l =C m , m + Cm 
,l ,
для чего входим в 
-строку и складываем диагональный элемент строки 
и элемент 
. Находим минимум 
, затем столбец l i помечаем значением мультииндекса , а диагональному элементу столбца l i придаем значение 
= 
. И так до тех пор, пока не пометим вершину t.
Заключительный шаг. Искомый путь определяем, двигаясь от t к S по отметкам вершин.
Программа даёт возможность студенту пройти режим обучения, затем проверить свои знания в режиме контроля. В обоих режимах можно посмотреть структуру графа.
Лабораторная работа № 3
Кратчайший остов графа
|
|
Теоретическая часть
Понятие дерева
Одним из наиболее важных понятий теории графов является дерево. Его упрощенное определение можно дать так. Дерево – граф, имеющий начало, от которого дуги (ребра) расходятся, как ветви дерева. Дерево, как и граф, может быть ориентированным и неориентированным.
Неориентированное дерево – это сильно связный граф, не имеющий циклов. Ориентированное дерево представляет собой ориентированный граф без циклов, в котором в каждую вершину должна быть направлена только одна дуга, кроме корневой вершины, куда не заходит ни одна дуга. Остовное дерево графа, или остов графа, имеет то же самое множество вершин, что и исходный граф, но множество дуг (ребер) остовного дерева является подмножеством множества дуг (ребер) исходного графа.