Следующим этапом моего исследования было построение трендовой модели для распределения во времени имеющихся факторов:
2.1 Трендовая модель для У (объем продаж ОАО "КрасЦветМет" в тыс. р.) и T(номера наблюдения)
Y=19057,66+15406,22*√T
| Beta | Std.Err.of Beta | B | Std.Err. of B | t(22) | p-level | |
| Intercept | 19057,66 | 7532,861 | 2,529937 | 0,019075 | ||
| SQRV2 | 0,838955 | 0,116024 | 15406,22 | 2130,615 | 7,230881 | 0,000000 |
Multipl R2=0,70384588- коэффициент детерминации близок к 1 следовательно уравнение качественное.

А так как коэффициент Durbin-Watson= 1,660515, то есто близок к 2 следовательно автокорреляции нет, и остатки независимы между собой. Учитывая нормальные характеристики уравнения регрессии можно составить прогноз.

Из данной таблицы следует, что с вероятностью 95% Y (объем продаж ОАО "КрасЦветМет" в тыс. руб.) в 25 периоде (т. е. на 01.08) будет варьироваться в промежутке от 86170,4 до 102894,5 тыс. руб.
2.2 Затем построим трендовую модель для Х1(затраты на изготовление календарей в тыс. руб.) и T(номер наблюдения)
| Beta | Std.Err.of Beta | B | Std.Err. of B | t(22) | p-level | |
| Intercept | 89,12270 | 29,70670 | 3,000087 | 0,006593 | ||
| V2**4 | 0,281994 | 0,204548 | 0,00034 | 0,00025 | 1,378620 | 0,181870 |
Х1=89,12270+0,00034*T4
Multipl R2=0,36351875 - коэффициент детерминации совсем не близок к 1 следовательно уравнение не качественное.
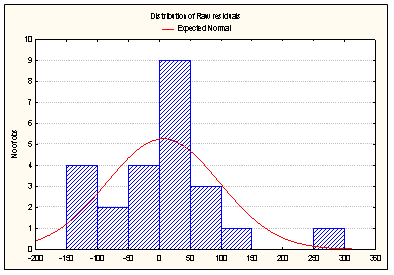
| Durbin-Watson d (Spreadsheet1) and serial correlation of residuals | |||
| Durbin- Watson d | Serial Corr. | ||
| Estimate | 2,435416 | -0,255076 |
Коэффициент Durbin-Watson= 2,435416, то есть близок к 2 следовательно автокорреляции нет, и остатки независимы между собой.
Характеристики уравнения не удовлетворяют условию нормальности, по этому на мой взгляд, не имеет смысла делать прогноз на будущий период.
2.3 Построим трендовую модель для Х2(затраты на наружную рекламу в тыс. руб..) и T(номер наблюдения)
Х2=-12,0434-0,1776*T2+84,8512\T+7,3503*T
| Regression Summary for Dependent Variable: X2 (Spreadsheet1) R=,68649810 R?=,47127964 Adjusted R?=,39197159 F(3,20)=5,9424 p<,00455 Std.Error of estimate: 14,304 | |||||||
| Beta | Std.Err.of Beta | B | Std.Err. of B | t(20) | p-level | ||
| Intercept | -12,0434 | 20,96019 | -0,57458 | 0,571981 | |||
| V2**2 | -1,76343 | 0,959260 | -0,1776 | 0,09664 | -1,83832 | 0,080915 | |
| 1/V2 | 0,96934 | 0,314012 | 84,8512 | 27,48697 | 3,08696 | 0,005814 | |
| T | 2,83339 | 1,104995 | 7,3503 | 2,86657 | 2,56416 | 0,018504 |
Multipl R2=0,47127964 - коэффициент детерминации не близок к 1 следовательно уравнение не качественное.

| Durbin-Watson d (Spreadsheet1) and serial correlation of residuals | |||
| Durbin- Watson d | Serial Corr. | ||
| Estimate | 1,885253 | 0,050585 |
А так как коэффициент Durbin-Watson= 1,885253, то есто близок к 2 следовательно автокорреляции нет, и остатки независимы между собой.
| Predicting Values for (Spreadsheet1) variable: X2 | |||
| B-Weight | Value | B-Weight * Value | |
| V2**2 | -0,17765 | 576,0000 | -102,325 |
| 1/V2 | 84,85116 | 0,4167 | 35,355 |
| № | 7,35035 | 24,0000 | 176,408 |
| Intercept | -12,043 | ||
| Predicted | 97,395 | ||
| -95,0%CL | 74,059 | ||
| +95,0%CL | 120,730 |
Из данной таблицы следует, что с вероятностью 95% Х2- затраты на наружную рекламу в тыс. руб. в 25 периоде (т. е. на 01.08) будет варьироваться в промежутке от 74,059 до 120,730 тыс. руб.
2.4 Построим трендовую модель для Х3(затраты на проведение выставок в тыс. руб.) и T(номер наблюдения)
Х3=-238,7172+1151,882\T
| Regression Summary for Dependent Variable: X3 (Spreadsheet1) R=,30199164 R?=,09119895 Adjusted R?=,04988981 F(1,22)=2,2077 p<,15151 Std.Error of estimate: 779,12 | |||||||
| Beta | Std.Err. of Beta | B | Std.Err. of B | t(22) | p-level | ||
| Intercept | 238,717 | 200,4239 | 1,191058 | 0,246323 | |||
| 1/V2 | 0,301992 | 0,203246 | 1151,882 | 775,2402 | 1,485839 | 0,151512 |
Multipl R2=0,09119895 - коэффициент детерминации совсем не близок к 1 следовательно уравнение не качественное.

| Durbin-Watson d (Spreadsheet1) and serial correlation of residuals | |||
| Durbin- Watson d | Serial Corr. | ||
| Estimate | 2,513233 | -0,351870 |
А так как коэффициент Durbin-Watson= 2,513233, то есто близок к 2 следовательно автокорреляции нет, и остатки независимы между собой.
Характеристики уравнения не удовлетворяют условию нормальности, по этому на мой взгляд, не имеет смысла делать прогноз на будущий период.