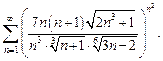РЯДЫ
Числовые ряды. Знакоположительные ряды
Понятие числовогоряда
Числовым рядом называется выражение вида
 (28.1)
(28.1)
где  – последовательность чисел,
– последовательность чисел, 


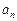 – n -й член ряда. Аналитическое выражение n -го члена в виде формулы называется общим членом ряда.
– n -й член ряда. Аналитическое выражение n -го члена в виде формулы называется общим членом ряда.
Ряд (28.1) называется знакопостоянным, если все его члены имеют одинаковый знак; знакопеременным – если члены ряда имеют различные знаки; знакоположительным – если все члены ряда положительны.
Сумма первых n членов ряда
 (28.2)
(28.2)
называется его n-й частичной суммой.
Ряд называется сходящимся, если последовательность  его частичных сумм имеет предел:
его частичных сумм имеет предел: 
Значение S называется суммой ряда, что записывают

Если для последовательности  предел при
предел при  не существует или он бесконечно большой, то ряд (28.1) называется расходящимся. Расходящийся ряд суммы не имеет.
не существует или он бесконечно большой, то ряд (28.1) называется расходящимся. Расходящийся ряд суммы не имеет.
Ряд
 (28.3)
(28.3)
который получается из исходного (28.1) отбрасыванием первых n последовательных членов, называется n-м остатком ряда.
Если ряд сходится (расходится), то и любой его остаток сходится (расходится).
Если ряды  и
и  сходятся к суммам
сходятся к суммам  соответственно, то ряд
соответственно, то ряд  сходится к сумме
сходится к сумме  где
где 

Необходимое условие сходимости. Если ряд (28.1) сходится, то его общий член стремится к нулю при неограниченном возрастании n:
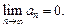
С л е д с т в и е. Если общий член ряда не стремится к нулю при неограниченном возрастании n, т. е. 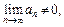 то ряд расходится.
то ряд расходится.
Исследование ряда на сходимость целесообразно начинать с необходимого условия сходимости. В случае его выполнения исследование продолжается с помощью достаточных признаковсходимости.
Достаточные признаки сходимости
знакоположительных рядов
Признак сравнения. Пусть заданы два знакоположительных ряда
 (28.4)
(28.4)
и
 (28.5)
(28.5)
для которых, начиная с некоторого n  выполняется условие
выполняется условие
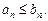 (28.6)
(28.6)
Тогда:
1) из сходимости ряда (28.5) следует сходимость ряда (28.4);
2) из расходимости ряда (28.4) следует расходимость ряда (28.5).
Если выполняется условие (28.6), то ряд (28.5) называется мажорантой для ряда (28.4).
Предельный признак сравнения. Если для знакоположительных рядов (28.4) и (28.5) существует конечный, отличный от нуля предел  то эти ряды одновременно сходятся или одновременно расходятся. Если
то эти ряды одновременно сходятся или одновременно расходятся. Если  то из сходимости ряда (28.5) следует сходимость ряда (28.4).
то из сходимости ряда (28.5) следует сходимость ряда (28.4).
Сравнение исследуемых рядов производится обычно с рядом, представляющим сумму членов геометрической прогрессии

который при  сходится, а при
сходится, а при  расходится, а также рядом Дирихле
расходится, а также рядом Дирихле

который при  сходится, а при
сходится, а при  расходится. В частном случае при
расходится. В частном случае при  получается гармонический ряд
получается гармонический ряд

который расходится.
Признак Д’Аламбера. Если для знакоположительного ряда (28.4), начиная с некоторого номера n  справедлива оценка
справедлива оценка

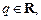
то ряд (28.4) сходится, если же справедливо условие

то ряд расходится.
Предельный признак Д’Аламбера. Пусть для знакоположительного ряда (28.4) существует
 (28.7)
(28.7)
Тогда:
1) при 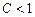 ряд сходится;
ряд сходится;
2) при  ряд расходится.
ряд расходится.
Признак Коши. Если для знакоположительного ряда (28.4), начиная с некоторого номера n  справедлива оценка
справедлива оценка

то ряд сходится, если же выполняется условие

то ряд расходится.
Предельный признак Коши. Пусть для знакоположительного ряда (28.4) существует
 (28.8)
(28.8)
Тогда:
1) при 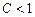 ряд сходится;
ряд сходится;
2) при  ряд расходится.
ряд расходится.
При использовании предельного признака Коши полезна формула

При  предельные признаки Д’Аламбера и Коши не дают ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуют по другим признакам.
предельные признаки Д’Аламбера и Коши не дают ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуют по другим признакам.
Интегральный критерий сходимости. Ряд с положительными монотонно убывающими членами  сходится (расходится) тогда и только тогда, когда несобственный интеграл
сходится (расходится) тогда и только тогда, когда несобственный интеграл  сходится (расходится), где f (x) – непрерывная убывающая функция.
сходится (расходится), где f (x) – непрерывная убывающая функция.
С л е д с т в и е. Если члены сходящегося знакоположительного ряда (28.4) монотонно убывают, то для n -го остатка  ряда справедлива оценка:
ряда справедлива оценка:

Пример 1. Исследовать сходимость ряда и в случае сходимости, найти его сумму:
1)  2)
2)  3)
3)  4)
4) 
Решение. 1) Разложим общий член ряда на простые дроби и приведем их к общему знаменателю:

Числители в левой и правой частях полученного выражения будут тождественно равны. Приравнивая коэффициенты при одинаковых степенях n в обеих частях числителей тождества, получим систему уравнений

решение которой: 
Тогда 
Запишем n -ю частичную сумму ряда:

Так как 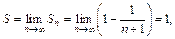
то данный ряд сходится к сумме 
2) Разложим общий член ряда на простые дроби и приведем их к общему знаменателю:
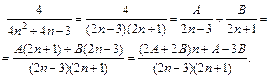
Числители в левой и правой частях полученного выражения будут тождественно равны. Приравнивая коэффициенты при одинаковых степенях n в обеих частях числителей тождества, получим систему уравнений

решение которой: А = 1, В = –1.
Тогда 
Выпишем n первых членов ряда:

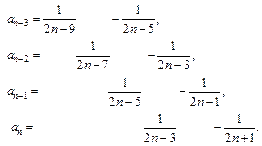
Сложив записанные члены ряда, получим:

Данный ряд сходится к сумме 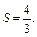
3) Данный ряд представляет собой сумму членов бесконечно убывающей геометрической прогрессии:
 со знаменателем
со знаменателем  Известно, что бесконечно убывающая геометрическая прогрессия с первым членом
Известно, что бесконечно убывающая геометрическая прогрессия с первым членом  и знаменателем q имеет конечную сумму, которую вычисляем по формуле
и знаменателем q имеет конечную сумму, которую вычисляем по формуле
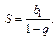
Значит, 
Данный ряд сходится к сумме 
4) Преобразуем общий член ряда:

Запишем n -ю частичную сумму ряда:

Так как 
то данный ряд суммы не имеет и является расходящимся.
Пример 2. Проверить выполнение необходимого признака сходимости для ряда:
1) 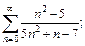 2)
2) 
В случае его выполнения продолжить исследование на сходимость.
Решение. Найдем предел общего члена ряда при неограниченном увеличении его номера n:
1) 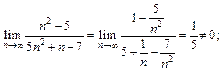
2) 
Первый ряд расходится, поскольку для него не выполняется необходимый признак сходимости. Для второго ряда необходимый признак сходимости выполняется, поэтому ряд может сходиться, а может и расходиться. Для установления сходимости оценим его n -ю частичную сумму:


Поскольку  то второй ряд также расходится.
то второй ряд также расходится.
Пример 3. Исследовать по признакам сравнения сходимость ряда:
1)  2)
2)  3)
3)  4)
4) 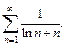
Решение. 1) Сравним заданный ряд со сходящейся геометрической прогрессией 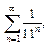 где
где  Замечаем, что каждый член
Замечаем, что каждый член  данного ряда меньше соответствующего члена
данного ряда меньше соответствующего члена  бесконечно убывающей геометрической прогрессии. Поэтому, согласно признаку сравнения, заданный ряд сходится.
бесконечно убывающей геометрической прогрессии. Поэтому, согласно признаку сравнения, заданный ряд сходится.
2) Сравним заданный ряд с расходящимся гармоническим рядом  где
где  Замечаем, что каждый член
Замечаем, что каждый член  заданного ряда больше соответствующего члена
заданного ряда больше соответствующего члена  расходящегося гармонического ряда. Поэтому, согласно признаку сравнения, заданный ряд расходится.
расходящегося гармонического ряда. Поэтому, согласно признаку сравнения, заданный ряд расходится.
3) Сравнив заданный ряд со сходящимся рядом Дирихле  где
где 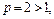 по предельному признаку сравнения, имеем:
по предельному признаку сравнения, имеем:

Получен конечный, отличный от нуля предел. Сравниваемые ряды ведут себя одинаково. Поэтому, согласно предельному признаку сравнения, заданный ряд сходится.
4) Воспользуемся предельным признаком сравнения с гармоническим рядом:

Получен конечный, отличный от нуля предел. Сравниваемые ряды ведут себя одинаково. Поэтому, согласно предельному признаку сравнения, заданный ряд расходится.
Пример 4. Исследовать по признаку Д’Аламбера сходимость ряда:
1)  2)
2)  3)
3) 
Решение. Используем предельный признак Д’Аламбера. Заменяем в заданной формуле общего члена ряда  номер n на n + 1 и получаем формулу следующего члена ряда
номер n на n + 1 и получаем формулу следующего члена ряда  Затем находим предел отношения последующего члена ряда
Затем находим предел отношения последующего члена ряда  к предыдущему
к предыдущему  при неограниченном увеличении номера n:
при неограниченном увеличении номера n:
1) 

Согласно предельному признаку Д’Аламбера, заданный ряд сходится.
2) Поскольку  и
и  то
то

Согласно предельному признаку Д’Аламбера, заданный ряд расходится.
3) По условию  и
и 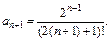 Поэтому
Поэтому

Согласно предельному признаку Д’Аламбера, заданный ряд сходится.
Пример 5. Исследовать по признаку Коши сходимость ряда:
1)  2)
2)  3)
3) 
Решение. 1) Используем предельный признак Коши.
По условию  Поэтому
Поэтому

Согласно предельному признаку Коши, заданный ряд сходится.
2) Поскольку  то
то

Согласно предельному признаку Коши, заданный ряд расходится.
3) Используя то, что 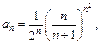 вычисляем:
вычисляем:

Согласно предельному признаку Коши, заданный ряд сходится.
Пример 6. Исследовать по интегральному критерию сходимость ряда:
1)  2)
2)  3)
3) 
Решение. 1) Заменяем в заданной формуле общего члена ряда  номер n на переменную x. Получаем
номер n на переменную x. Получаем  где
где  Убеждаемся, что полученная функция f (x) является непрерывной и убывающей на бесконечном интервале изменения x. Затем исследуем на сходимость несобственный интеграл
Убеждаемся, что полученная функция f (x) является непрерывной и убывающей на бесконечном интервале изменения x. Затем исследуем на сходимость несобственный интеграл 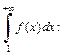
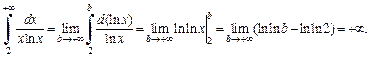
Поскольку интеграл расходится, то, согласно интегральному критерию, заданный ряд также расходится.
2) Изучим сходимость соответствующего несобственного интеграла:

Несобственный интеграл 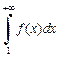 сходится, а следовательно, сходится и заданный ряд.
сходится, а следовательно, сходится и заданный ряд.
3) Исследуем на сходимость соответствующий несобственный интеграл:

Несобственный интеграл  расходится, а следовательно, расходится и заданный ряд.
расходится, а следовательно, расходится и заданный ряд.
Пример 7. Вычислить приближенное значение суммы ряда  с точностью до 0,1.
с точностью до 0,1.
Решение. Воспользуемся оценкой остатка ряда:
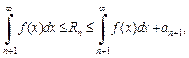


Чтобы обеспечить точность в 0,1, нужно взять 10 членов ряда, так как 
Получаем

Задания
I уровень
1.1. Напишите пять первых членов ряда, и проверьте, выполняется ли для него необходимый признак сходимости:
1)  2)
2) 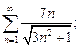 3)
3) 
4)  5)
5) 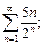 6)
6) 
1.2. Исследуйте сходимость ряда по признакам сравнения:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
1.3. Исследуйте сходимость ряда по признаку Д’Аламбера:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
1.4. Исследуйте сходимость ряда по признаку Коши:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
1.5. Исследуйте сходимость ряда по интегральному критерию:
1)  2)
2)  3)
3) 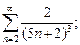
4)  5)
5)  6)
6) 
II уровень
2.1. Найдите сумму ряда:
1) 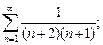 2)
2) 
3)  4)
4) 
5) 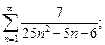 6)
6) 
2.2. Исследуйте сходимость ряда по признакам сравнения:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
2.3. Исследуйте сходимость ряда по признаку Д’Аламбера:
1)  2)
2)  3)
3) 
4) 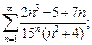 5)
5)  6)
6) 
2.4. Исследуйте сходимость ряда по признаку Коши:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
2.5. Исследуйте сходимость ряда по интегральному критерию:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
2.6. Исследуйте сходимость ряда с положительными членами:
1) 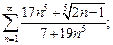 2)
2) 
3)  4)
4) 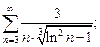
5)  6)
6) 
7)  8)
8) 
9) 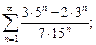 10)
10) 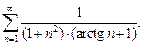
III уровень
3.1. Найдите сумму ряда:
1) 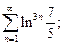 2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  .
.
3.2. Исследуйте сходимость ряда с положительными членами:
1)  2)
2) 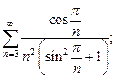
3)  4)
4) 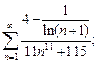
5)  6)
6) 
7)  8)
8) 
9)  10)
10)