1. Сумма S (x) степенного ряда является непрерывной функцией на его интервале сходимости.
2. Степенной ряд с суммой S (x) можно почленно дифференцировать и интегрировать на его интервале сходимости любое количество раз:
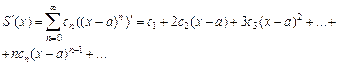
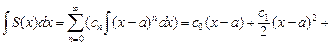

Интервал сходимости при этом не меняется. Сходимость может измениться только в граничных точках интервала сходимости.
Операции почленного дифференцирования и интегрирования позволяют в некоторых случаях найти сумму степенного ряда.
Если существует такой степенной ряд (28.18), который на определенном промежутке D сходится к функции f (x), то говорят, что функция f (x) разлагается на промежутке D в степенной ряд (по степеням x – a), а выражение вида
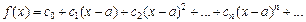 , (28.20)
, (28.20)
где  называется разложением функции в степенной ряд (по степеням x – a). Такое разложение единственно.
называется разложением функции в степенной ряд (по степеням x – a). Такое разложение единственно.
Рядом Тейлора функции f (x) в окрестности точки a (по степенямx – a), называется степенной ряд вида
 (28.21)
(28.21)
Критерий сходимости ряда Тейлора. Ряд Тейлора (28.21) функции f (x)сходится к ней на некотором интервале  тогда и только тогда, когда остаточный член
тогда и только тогда, когда остаточный член  формулы Тейлора для функции f (x) при всех
формулы Тейлора для функции f (x) при всех 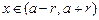 стремится к нулю с ростом n:
стремится к нулю с ростом n: 
Признак сходимости ряда Тейлора. Если в интервале  функция f (x)бесконечно дифференцируема и все ее производные ограничены в совокупности, то в этом интервале функция f (x)разлагается в ряд Тейлорапо степеням
функция f (x)бесконечно дифференцируема и все ее производные ограничены в совокупности, то в этом интервале функция f (x)разлагается в ряд Тейлорапо степеням  (является его суммой).
(является его суммой).
Рядом Маклорена функции f (x) называется ряд Тейлора (28.21) функции f (x)в окрестности точки  (по степеням x):
(по степеням x):
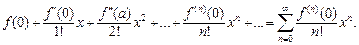 (28.22)
(28.22)
На области сходимости ряды Маклорена для основных элементарных функций имеют указанный ниже вид:
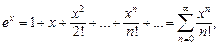
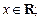
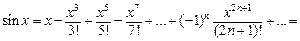
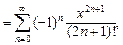
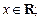

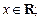
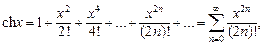
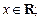

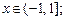

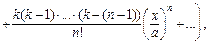
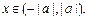
При разложении функции f (x) в ряд используют следующие правила:
1) непосредственное разложение функции f (x) вряд Тейлора (28.21) или Маклорена (28.22);
2) использование известных рядов Маклорена для основных элементарных функций;
3) использование сложения и вычитания рядов и умножения ряда на число;
4) использование дифференцирования и интегрирования рядов.
Пример 1. Найти область сходимости степенного ряда:
1) 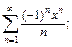 2)
2) 
3)  4)
4) 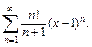
Решение. 1) Формула коэффициентов ряда: 
По формуле (28.19) найдем радиус сходимости степенного ряда:

Поэтому (–1; 1) является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (–1; 1). При  получаем гармонический ряд, который расходится:
получаем гармонический ряд, который расходится:
 .
.
При 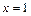 получаем знакочередующийся ряд, который сходится по признаку Лейбница:
получаем знакочередующийся ряд, который сходится по признаку Лейбница:
 .
.
Следовательно, областью сходимости данного ряда является полуоткрытый интервал 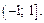
2) Имеем степенной ряд с центром в точке 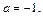
Формула коэффициентов ряда 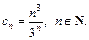
По формуле (28.19) найдем радиус сходимости степенного ряда:
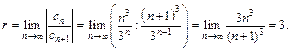
Поэтому 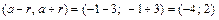 является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (–4; 2). При
является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (–4; 2). При  получаем знакочередующийся ряд
получаем знакочередующийся ряд 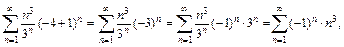 который расходится, поскольку для него не выполняется необходимый признак сходимости:
который расходится, поскольку для него не выполняется необходимый признак сходимости: 
При  получаем знакоположительный ряд
получаем знакоположительный ряд
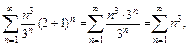
который также расходится, поскольку для него не выполняется необходимый признак сходимости.
Следовательно, областью сходимости заданного ряда является открытый интервал: (–4; 2).
3) Имеем степенной ряд с центром в точке  Формула коэффициентов ряда
Формула коэффициентов ряда 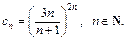 По формуле (28.19) найдем радиус сходимости степенного ряда:
По формуле (28.19) найдем радиус сходимости степенного ряда:
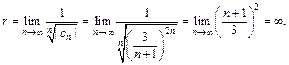
Следовательно, областью сходимости заданного ряда является вся числовая ось: 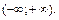
4) Имеем степенной ряд с центром в точке 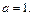 Формула коэффициентов ряда:
Формула коэффициентов ряда: 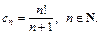 По формуле (28.19) найдем радиус сходимости степенного ряда:
По формуле (28.19) найдем радиус сходимости степенного ряда:

Следовательно, заданный ряд сходится только в точке 
Пример 2. Найти сумму ряда и указать область сходимости:
1) 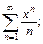 2)
2) 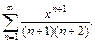
Решение. 1) Интервал сходимости заданного ряда: (– 1; 1). Значит, его можно почленно дифференцировать и интегрировать в его интервале сходимости. Выполним дифференцирование:
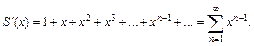
Полученный ряд представляет собой сумму бесконечно убывающей при 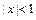 геометрической прогрессии:
геометрической прогрессии:
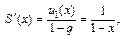 откуда
откуда 
Таким образом, сумма заданного ряда 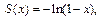
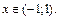
2) Область сходимости заданного ряда [–1; 1], что следует из признака абсолютной сходимости Д’Аламбера и сходимости ряда при 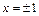 (убедитесь в этом самостоятельно). Значит, его можно почленно дифференцировать и интегрировать в его интервале сходимости:
(убедитесь в этом самостоятельно). Значит, его можно почленно дифференцировать и интегрировать в его интервале сходимости:

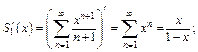

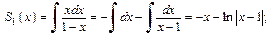

Окончательно имеем:

Пример 3. Разложить функцию  в ряд Тейлора по степеням x.
в ряд Тейлора по степеням x.
Решение. Используем прием непосредственного разложения.
Составим для данной функции ряд Тейлора. С этой целью найдем числовые значения производных всех порядков функции в точке 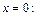

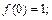


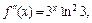

..............................

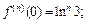
..............................
Подставив найденные значения производных в выражение (28.21) при 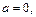 получим ряд Тейлора для функции
получим ряд Тейлора для функции 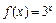 по степеням x:
по степеням x:
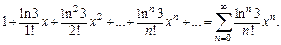
По формуле (28.19) найдем радиус сходимости полученного степенного ряда:

Следовательно, областью сходимости данного ряда является вся числовая ось: 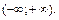
Пример 4. Разложить функцию 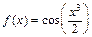 в ряд Маклорена.
в ряд Маклорена.
Решение. Полагаем 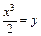 и используем известное разложение в ряд Маклорена для функции
и используем известное разложение в ряд Маклорена для функции 
 .
.
Тогда, с учетом того, что 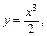 получаем:
получаем:
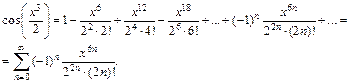
Так как разложение в ряд Маклорена функции 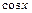 имеет место для всех
имеет место для всех 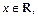 то и разложение в ряд Маклорена заданной функции
то и разложение в ряд Маклорена заданной функции 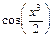 имеет место для всех
имеет место для всех 
Пример 5. Разложить в ряд по степеням x функцию 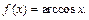
Решение. Замечаем, что функцию  можно получить интегрированием функции
можно получить интегрированием функции  Поэтому разложим в ряд по степеням x функцию
Поэтому разложим в ряд по степеням x функцию 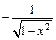 и затем проинтегрируем полученный степенной ряд. Поскольку
и затем проинтегрируем полученный степенной ряд. Поскольку  используем табличное разложение для функции
используем табличное разложение для функции 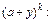

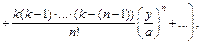

Полагая 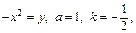 получим:
получим:


Так как при интегрировании интервал сходимости степенного ряда не меняется, то найденное разложение имеет место для 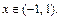
Пример 6. Разлагая функцию 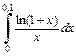 в ряд, вычислить с точностью 0,001.
в ряд, вычислить с точностью 0,001.
Решение. Используя разложение 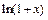 в степенной ряд, получим
в степенной ряд, получим
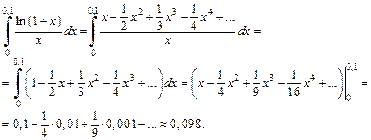
Мы взяли два слагаемых, так как третье по модулю меньше требуемой точности  Поэтому, начиная с третьего, все последующие слагаемые отбрасываем.
Поэтому, начиная с третьего, все последующие слагаемые отбрасываем.
Задания
I уровень
1.1. Найдите область сходимости степенного ряда:
1) 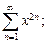 2)
2)  3)
3) 
4) 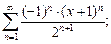 5)
5) 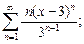 6)
6) 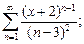
7)  8)
8) 
1.2. Найдите первые четыре члена разложения функции в ряд Маклорена и укажите область сходимости полученного ряда к своей сумме:
1) 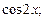 2)
2)  3)
3)  4)
4)  5)
5) 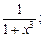
6) 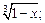 7)
7) 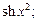 8)
8) 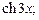 9)
9) 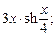 10)
10) 
1.3. Пользуясь соответствующими рядами, вычислите приближенно с точностью до α:
1)  2)
2) 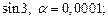 3)
3) 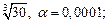
4)  5)
5) 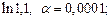 6)
6) 
7) 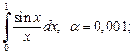 8)
8) 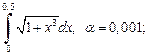
9) 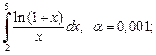 10)
10) 
II уровень
2.1. Найдите область сходимости степенного ряда:
1) 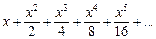 ; 2)
; 2) 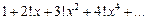 ;
;
3)  4)
4) 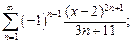
5)  6)
6) 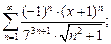
7) 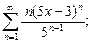 8)
8) 
2.2. Найдите сумму ряда и укажите область сходимости к своей сумме:
1) 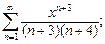 2)
2) 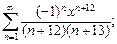
3)  4)
4) 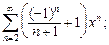
5)  6)
6) 
7) 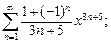 8)
8) 
2.3. Найдите первые четыре члена разложения функции в ряд Маклорена и укажите область сходимости полученного ряда к своей сумме:
1)  2)
2)  3)
3)  4)
4) 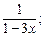 5)
5) 
6)  7)
7)  8)
8) 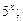 9)
9) 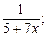 10)
10) 
2.4. Пользуясь соответствующими рядами, вычислите приближенно с точностью до α:
1) 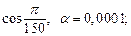 2)
2) 
3) 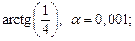 4)
4) 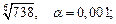
5) 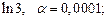 6)
6) 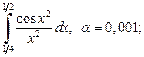
7)  8)
8) 
III уровень
3.1. Найдите область сходимости степенного ряда:
1) 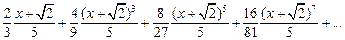 ;
;
2) 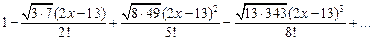 ;
;
3)  4)
4) 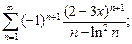
5) 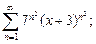 6)
6) 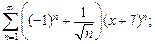
7)  8)
8) 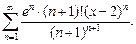
3.2. Найдите сумму ряда и укажите область сходимости к своей сумме:
1) 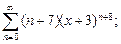 2)
2) 
3)  4)
4) 
5) 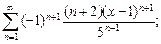 6)
6) 
7)  8)
8) 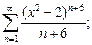
9)  10)
10) 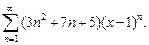
3.3. Найдите первые пять членов разложения функции в ряд Тейлора в окрестности указанной точки a и укажите область сходимости полученного ряда к своей сумме:
1) 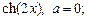 2)
2) 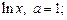 3)
3) 
4)  5)
5) 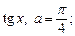 6)
6) 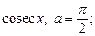
7) 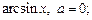 8)
8) 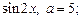 9)
9) 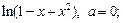
10) 
3.4. Пользуясь соответствующими рядами, вычислите приближенно с точностью до α:
1) 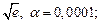 2)
2) 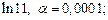 3)
3) 
4) 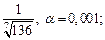 5)
5)  6)
6) 
7)  8)
8) 
9) 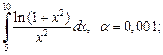 10)
10) 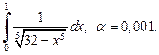
Ряд Фурье
Рядом Фурье 2 π-периодической функции f (x) называется ряд
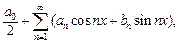 (28.23)
(28.23)
где
 (28.24)
(28.24)
 (28.25)
(28.25)
 (28.26)
(28.26)
Числа (28.24)–(28.26) называются коэффициентами Фурье.
Это записывается следующим образом:
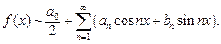
Сумма такого ряда S (x), если она существует, является периодической функцией от x с периодом 2 π.
Достаточные условия сходимости ряда Фурье сформулированы в теореме Дирихле.
Теорема Дирихле. Пусть 2 π -периодическая функция f (x) на промежутке 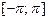 имеет конечное число точек разрыва первого рода
имеет конечное число точек разрыва первого рода 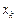 (или непрерывна) и конечное число точек экстремума (или кусочно-монотонна). Тогда ее ряд Фурье сходится (т. е. имеет сумму S (x)) во всех точках этого интервала. При этом:
(или непрерывна) и конечное число точек экстремума (или кусочно-монотонна). Тогда ее ряд Фурье сходится (т. е. имеет сумму S (x)) во всех точках этого интервала. При этом:
1) в точках непрерывности ряд Фурье сходится к самой функции:

2) в каждой точке разрыва 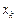 функции ее ряд Фурье сходится к полусумме односторонних пределов функции при стремлении x к
функции ее ряд Фурье сходится к полусумме односторонних пределов функции при стремлении x к  слева и справа:
слева и справа:
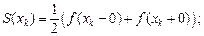
3) в граничных точках промежутка 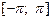 ряд Фурье сходится к полусумме односторонних пределов функции при стремлении x к этим точкам изнутри промежутка:
ряд Фурье сходится к полусумме односторонних пределов функции при стремлении x к этим точкам изнутри промежутка:

Частные случаи разложения функции f (x), удовлетворяющей условиям теоремы Дирихле, в ряд Фурье следующие:
1. Если функция f (x) является четной 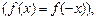 то ее ряд Фурье содержит только косинусы
то ее ряд Фурье содержит только косинусы 
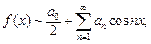 (28.27)
(28.27)
где 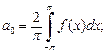
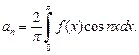
2. Если функция f (x) является нечетной 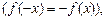 то ее ряд Фурье содержит только синусы
то ее ряд Фурье содержит только синусы 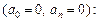
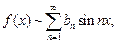 (28.28)
(28.28)
где 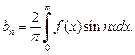
3. Если функция f (x) задана на промежутке  то ее ряд Фурье может быть получен различными способами, в зависимости от того, как построено продолжение функции на промежуток
то ее ряд Фурье может быть получен различными способами, в зависимости от того, как построено продолжение функции на промежуток 
При четном продолжении функции на промежуток  (график данной функции продолжается на промежуток
(график данной функции продолжается на промежуток  симметрично относительно оси ординат, рис. 28.1) получают ряд по косинусам (формула (28.27)).
симметрично относительно оси ординат, рис. 28.1) получают ряд по косинусам (формула (28.27)).
При нечетном продолжении функции на промежуток  (график данной функции продолжается на промежуток
(график данной функции продолжается на промежуток  симметрично относительно начала координат, рис. 28.2) получают ряд по синусам (формула (28.28)).
симметрично относительно начала координат, рис. 28.2) получают ряд по синусам (формула (28.28)).
 Рис. 28.1
Рис. 28.1
| 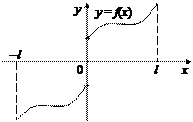 Рис. 28.2
Рис. 28.2
|
4. Для функции f (x), заданной на промежутке  ее ряд Фурье (28.23), получается при условии, что пределами интегрирования в формулах (28.24)–(28.26) являются 0 и 2π.
ее ряд Фурье (28.23), получается при условии, что пределами интегрирования в формулах (28.24)–(28.26) являются 0 и 2π.
5. Если функция f (x) задана несколькими различными формулами на промежутке  то при разложении ее в ряд Фурье, при вычислении интегралов в формулах (28.24)–(28.26) для коэффициентов ряда, следует разбить интервал интегрирования точками, в которых меняется аналитическое выражение функции, на части и вычислять интегралы как сумму интегралов по составляющим частям.
то при разложении ее в ряд Фурье, при вычислении интегралов в формулах (28.24)–(28.26) для коэффициентов ряда, следует разбить интервал интегрирования точками, в которых меняется аналитическое выражение функции, на части и вычислять интегралы как сумму интегралов по составляющим частям.
6. Если функция f (x) задана на произвольном промежутке  то ее ряд Фурье может быть получен двумя способами:
то ее ряд Фурье может быть получен двумя способами:
а) если построено продолжение функции на промежутке  четным образом (рис. 28.3), то разложение в ряд Фурье происходит по косинусам (формула (28.27));
четным образом (рис. 28.3), то разложение в ряд Фурье происходит по косинусам (формула (28.27));
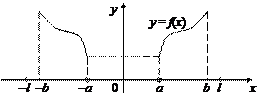
Рис. 28.3
б) если построено продолжение функции на промежутке 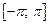 нечетным образом (рис. 28.4), то разложение в ряд Фурье происходит по синусам (формула (28.28)).
нечетным образом (рис. 28.4), то разложение в ряд Фурье происходит по синусам (формула (28.28)).
Рис. 28.4
7. Для функции f (x), заданной на произвольном промежутке [ a; b ] длины 2 π, ее ряд Фурье (28.23) получается при условии, что в формулах коэффициентов (28.24)–(28.26) пределами интегрирования являются числа а и b.
Если f (x) – 2 l -периодическая функция,  то ее ряд Фурье
то ее ряд Фурье
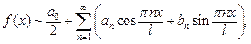 (28.29)
(28.29)
где 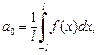 (28.30)
(28.30)
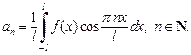 (28.31)
(28.31)
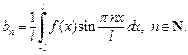 (28.32)
(28.32)
Ряд (28.23) является частным случаем ряда (28.29).
Как и в случае 2π -периодической функции четная 2 l -периодическая функция разлагается только по косинусам, нечетная – по синусам.
Теорема сходимости Дирихле обобщается на случай 2 l -периодической функции.
С помощью формул Эйлера




из формул (28.23)–(28.26) получается удобная своей краткостью комплексная форма ряда Фурье 2 l-периодической функции:
 (28.33)
(28.33)
где
 (28.34)
(28.34)
Пример 1. Разложить в ряд Фурье периодическую функцию (с периодом 2p):

Записать первые три члена полученного ряда. Исследовать ряд на сходимость.
Решение. Изобразим график заданной функции (рис. 28.5).
Поскольку функция f (x) не является ни четной, ни нечетной, то вычисляем ее коэффициенты Фурье по общим формулам (28.23)–(28.26):
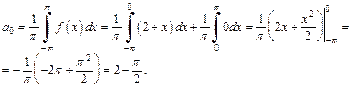

Рис. 28.5
Пусть  тогда
тогда
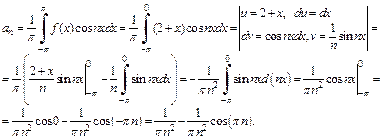
Так как  n = 0, 1, 2, …, то
n = 0, 1, 2, …, то
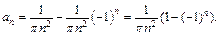
Вычисляем далее:

Таким образом, согласно формуле (28.23), искомый ряд Фурье функции f (x) имеет вид

Полагая последовательно n = 1, 2, 3, получаем:
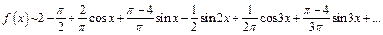
Заданная функция удовлетворяет условиям теоремы Дирихле. В точках ее непрерывности  ряд Фурье сходится к f (x). В точках разрыва
ряд Фурье сходится к f (x). В точках разрыва  сумма полученного ряда равна 1. Например, в точке х = 0, имеем
сумма полученного ряда равна 1. Например, в точке х = 0, имеем

В точках разрыва  сумма полученного ряда равна
сумма полученного ряда равна

График суммы S (x) ряда Фурье изображен на рис. 28.6.

Рис. 28.6
Пример 2. Разложить в ряд Фурье периодическую функцию с периодом 4:

Решение. Изобразим график заданной функции (рис. 28.7).
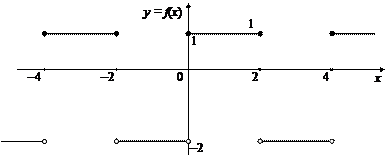
Рис. 28.7
Поскольку функция f (x) не является ни четной, ни нечетной, то вычисляем ее коэффициенты Фурье по общим формулам (28.29)–(28.32), полагая l = 2:
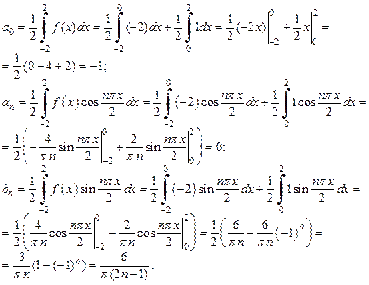
Таким образом, согласно формуле (28.29), искомый ряд Фурье функции f (x) имеет вид
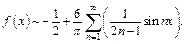
Функция f (x) удовлетворяет условиям теоремы Дирихле, поэтому в точках ее непрерывности 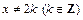 ряд Фурье сходится к f (x), а в точках разрыва
ряд Фурье сходится к f (x), а в точках разрыва 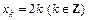 сумма полученного ряда равна –0,5:
сумма полученного ряда равна –0,5:
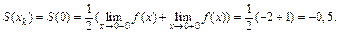
Пример 3. Разложить в ряд Фурье 2 p -периодическую функцию 
Решение. Изобразим график заданной функции (рис. 28.8)
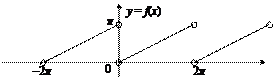
Рис. 28.8
Поскольку функция f (x) не является ни четной, ни нечетной, то вычисляем ее коэффициенты Фурье по общим формулам (28.29)–(28.32), полагая  (с пределами интегралов 0и 2 π), поскольку функция задана в интервале
(с пределами интегралов 0и 2 π), поскольку функция задана в интервале 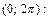
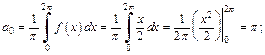
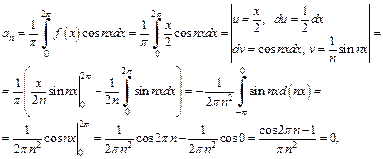
так как 

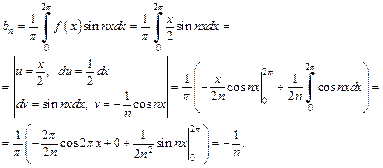
Таким образом, согласно формуле (28.29), искомый ряд Фурье функции f (x) имеет вид:
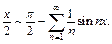
Функция f (x) удовлетворяет условиям теоремы Дирихле, поэтому в точках ее непрерывности 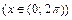 ряд Фурье сходится к f (x), а в граничных точках
ряд Фурье сходится к f (x), а в граничных точках  и
и 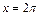 сумма полученного ряда равна
сумма полученного ряда равна 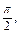 так как
так как
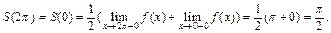
График суммы полученного ряда изображен на рис. 28.9.

Рис. 28.9
Пример 4. Разложить в ряд Фурье функцию 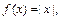
 считая ее заданной на периоде.
считая ее заданной на периоде.
Решение. Изобразим график заданной функции (рис. 28.10).

Рис. 28.10
Поскольку функция f (x) является четной, то вычисляем ее коэффициенты Фурье по формулам (28.29)–(28.32), учитывая, что ее ряд Фурьене содержит синусов 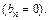 Полагаем
Полагаем  и берем пределами интегралов 0и 1, поскольку функция задана на отрезке
и берем пределами интегралов 0и 1, поскольку функция задана на отрезке 
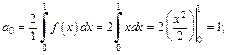

Отсюда следует, что  при четном n,
при четном n,  при нечетном n.
при нечетном n.
Таким образом, согласно формуле (28.29), искомый ряд Фурье функции f (x) имеет вид
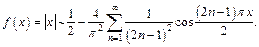
Функция f (x) удовлетворяет условиям теоремы Дирихле, поэтому в точках ее непрерывности ряд Фурье сходится к f (x) на всей числовой прямой.
Пример 5. Разложить в ряд Фурье функцию 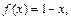 заданную на промежутке [0; 1], как на полупериоде:
заданную на промежутке [0; 1], как на полупериоде:
1) по синусам; 2) по косинусам.
Решение. 1) Продолжим заданную функцию на промежуток [– 1; 0] нечетным образом, т. е. положим

Далее продолжим ее периодически (рис. 28.11).
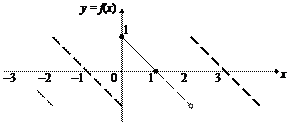
Рис. 28.11
Поскольку функция f (x) является нечетной, то ее ряд Фурьесодержит только синусы  Вычисляем его коэффициенты Фурье по формулам (28.28)–(28.31), полагая
Вычисляем его коэффициенты Фурье по формулам (28.28)–(28.31), полагая  Пределами интегралов берем 0и 1, поскольку функция задана на промежутке [0; 1]:
Пределами интегралов берем 0и 1, поскольку функция задана на промежутке [0; 1]:
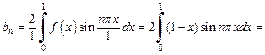
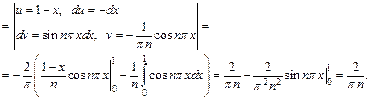
Таким образом, согласно формуле (28.28), искомый ряд Фурье функции f (x) имеет вид

2) Продолжим заданную функцию на промежуток [–1; 0] четным образом, т. е. положим

Затем продолжим его периодически (рис. 28.12).

Рис. 28.12
Поскольку функция f (x) является четной, то ее ряд Фурьесодержит только косинусы 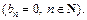 Вычисляем его коэффициенты Фурье по формулам (28.29)–(28.32), полагая
Вычисляем его коэффициенты Фурье по формулам (28.29)–(28.32), полагая 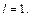 Пределами интегралов берем 0и 1, поскольку функция задана на промежутке [0; 1]:
Пределами интегралов берем 0и 1, поскольку функция задана на промежутке [0; 1]:


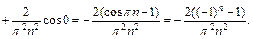
Откуда следует, что  при четном n,
при четном n,  при нечетном n.
при нечетном n.
Таким образом, согласно формуле (28.29), искомый ряд Фурье функции f (x) имеет вид:

Функция f (x) удовлетворяет условиям теоремы Дирихле, поэтому во всей области определения ряд Фурье сходится к f (x), а на всей числовой прямой сумма полученного ряда определяет периодическую функцию с периодом 2.
Пример 6. Разложить в ряд Фурье в комплексной форме 2 p -периодическую функцию 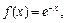
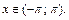
Решение. Изобразим график этой функции (рис. 28.13).

Рис. 28.13
По формуле (28.33) вычисляем

По формулам Эйлера 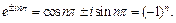
Следовательно, 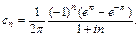
Таким образом, согласно формуле (28.32), искомый ряд Фурье функции f (x) имеет вид:
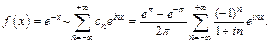
Функция f (x) удовлетворяет условиям теоремы Дирихле, поэтому в интервалах  ряд Фурье сходится к функции
ряд Фурье сходится к функции 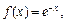 а в точках
а в точках 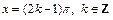 его сумма равна
его сумма равна

Задания
I уровень
1.1. Разложите в ряд Фурье периодическую функцию (с периодом 2 p). Запишите первые три его слагаемых. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)  2)
2) 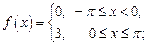
3) 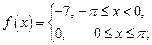 4)
4) 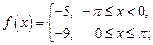
5) 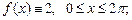 6)
6) 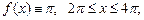
7) 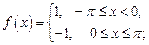 8)
8) 
1.2. Разложите в ряд Фурье функцию, заданную на промежутке  как на полупериоде:
как на полупериоде:
а) по синусам; б) по косинусам.
Запишите первые три члена полученного ряда. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1) 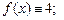 2)
2) 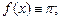 3)
3) 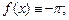
4)  5)
5)  6)
6) 
7) 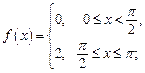 8)
8) 
II уровень
2.1. Разложите в ряд Фурье периодическую функцию (с периодом 2 p). Запишите первые три его слагаемых. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)  2)
2) 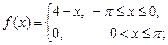
3)  4)
4) 
5) 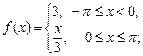 6)
6) 