Для знакопеременного ряда
 (28.9)
(28.9)
составляют ряд из абсолютных значений его членов, т. е.
 (28.10)
(28.10)
Для исследования на сходимость ряда (28.10) используют признаки сходимости знакоположительных рядов.
Знакопеременный ряд (28.9) называется абсолютно сходящимся, если сходится ряд (28.10).
Теорема. Всякий абсолютно сходящийся ряд сходится.
Если знакопеременный ряд не сходится абсолютно, то нельзя утверждать, что он не сходится. Необходимо провести дополнительное исследование.
Знакопеременный ряд называется условно сходящимся, если он сходится, но не сходится абсолютно.
Для исследования на сходимость знакопеременного ряда вида
 (28.11)
(28.11)
используют следующие две теоремы.
Признак Дирихле. Пусть для ряда (28.11) выполняются условия:
1) последовательность частичных сумм ряда  является ограниченной;
является ограниченной;
2) последовательность 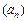 монотонно убывает, стремясь к нулю.
монотонно убывает, стремясь к нулю.
Тогда ряд (28.11) сходится.
Признак Абеля. Пусть для ряда (28.11) выполняются условия:
1) последовательность  является монотонной и ограниченной;
является монотонной и ограниченной;
2) ряд  сходится.
сходится.
Тогда ряд (28.11) сходится.
Важным частным случаем знакопеременного ряда является знакочередующийся ряд.
Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки.
Признак Лейбница. Пусть для знакочередующегося ряда
 (28.12)
(28.12)
где 
 выполняются условия:
выполняются условия:
1) абсолютные значения его членов образуют монотонно невозрастающую последовательность, т. е.

2) 
Тогда ряд (28.12) сходится.
Ряд, удовлетворяющий условиям признака Лейбница, называется рядом Лейбница.
С л е д с т в и е 1. Если для знакочередующегося ряда (28.12) выполняются условия признака Лейбница, то для его суммы S справедлива оценка 
С л е д с т в и е 2. Для остатка  знакочередующегося ряда, который удовлетворяет признаку Лейбница, справедлива оценка
знакочередующегося ряда, который удовлетворяет признаку Лейбница, справедлива оценка 

Пример 1. Исследовать сходимость знакопеременного ряда (определить, является ли он абсолютно сходящимся, условно сходящимся или расходящимся):
1)  2)
2)  3)
3)  4)
4) 
Решение. 1) Чтобы установить, сходится ли заданный ряд абсолютно, исследуем знакоположительный ряд  составленный из абсолютных величин членов данного ряда. Воспользуемся предельным признаком сравнения с расходящимся гармоническим рядом
составленный из абсолютных величин членов данного ряда. Воспользуемся предельным признаком сравнения с расходящимся гармоническим рядом 

Получен конечный, отличный от нуля предел. Сравниваемые ряды ведут себя одинаково. Поэтому, согласно предельному признаку сравнения, знакоположительный ряд из модулей расходится. Для исследования на условную сходимость используем признак Лейбница. Поскольку члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:  и
и  то, согласно признаку Лейбница, заданный ряд сходится. Следовательно, заданный ряд является условно сходящимся.
то, согласно признаку Лейбница, заданный ряд сходится. Следовательно, заданный ряд является условно сходящимся.
2) Исследуем знакоположительный ряд  составленный из абсолютных величин членов данного знакопеременного ряда. Поскольку
составленный из абсолютных величин членов данного знакопеременного ряда. Поскольку 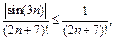 то воспользуемся признаком сравнения с рядом
то воспользуемся признаком сравнения с рядом 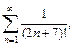 который, согласно предельному признаку Д’Аламбера, сходится. Действительно:
который, согласно предельному признаку Д’Аламбера, сходится. Действительно: 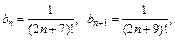

Поэтому, согласно признаку сравнения, полученный знакоположительный ряд также сходится, а значит, заданный ряд является абсолютносходящимся.
3) Чтобы установить, сходится ли заданный ряд абсолютно, исследуем знакоположительный ряд  составленный из абсолютных величин членов данного ряда. Используем интегральный критерий:
составленный из абсолютных величин членов данного ряда. Используем интегральный критерий:

Следовательно, заданный знакочередующийся ряд является абсолютносходящимся.
4) Для заданного знакопеременного ряда не выполняется необходимый признак сходимости:
 – не существует (
– не существует ( «колеблется» между –1 и 1, не стремясь ни к какому определенному числу). Следовательно, заданный знакопеременный ряд расходится.
«колеблется» между –1 и 1, не стремясь ни к какому определенному числу). Следовательно, заданный знакопеременный ряд расходится.
Пример 2. Установить сходимость ряда  и вычислить приближенное значение его суммы с точностью до 0,01.
и вычислить приближенное значение его суммы с точностью до 0,01.
Решение. Поскольку члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:  и
и  то согласно признаку Лейбница заданный ряд сходится. Чтобы обеспечить точность в 0,01, нужно вычислить несколько последовательных первых членов ряда, пока не получим такой член, абсолютное значение которого меньше
то согласно признаку Лейбница заданный ряд сходится. Чтобы обеспечить точность в 0,01, нужно вычислить несколько последовательных первых членов ряда, пока не получим такой член, абсолютное значение которого меньше 
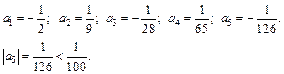
Следовательно, чтобы обеспечить точность до 0,01, нужно взять четыре члена ряда:

Задания
I уровень
1.1. Напишите пять первых членов знакопеременного ряда и исследуйте его сходимость (определите, является ли он абсолютно сходящимся, условно сходящимся или расходящимся):
1)  2)
2)  3)
3) 
4)  5)
5) 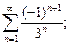 6)
6) 
7)  8)
8)  9)
9) 
10) 
1.2. Исследуйте сходимость ряда и вычислите приближенное значение его суммы с точностью до 0,01:
1)  2)
2) 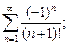 3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8)  9)
9) 
10) 
II уровень
2.1. Исследуйте сходимость знакопеременного ряда (определите, является ли он абсолютно сходящимся, условно сходящимся или расходящимся):
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8)  9)
9) 
10) 
2.2. Исследуйте сходимость ряда и вычислите приближенное значение его суммы с точностью до 0,01:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8) 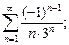 9)
9) 
10) 
III уровень
3.1. Исследуйте сходимость знакопеременного ряда (определите, является ли он абсолютно сходящимся, условно сходящимся или расходящимся):
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
3.2. Исследуйте сходимость ряда и вычислите приближенное значение его суммы с точностью до α:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 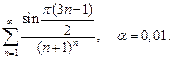
Функциональные ряды
Функциональным рядом называется выражение вида
 (28.13)
(28.13)
где 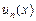 – функции, определенные на числовом множестве
– функции, определенные на числовом множестве 

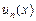 – n -й член ряда.
– n -й член ряда.
Сумма первых n членов ряда
 (28.14)
(28.14)
называется его n-йчастичной суммой.
Ряд
 (28.15)
(28.15)
называется n-мостатком ряда.
При определенном значении x выражение (28.13) является числовым рядом.
В зависимости от значения x выражение (28.13) становится сходящимся или расходящимся числовым рядом. Совокупность всех тех значений x  для которых ряд (28.13) сходится, называется областью сходимости ряда и обозначается D:
для которых ряд (28.13) сходится, называется областью сходимости ряда и обозначается D: 
Если 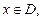 то можно говорить о сумме ряда (28.13) в точке x:
то можно говорить о сумме ряда (28.13) в точке x:  т. е. значение суммы ряда зависит от аргумента x.
т. е. значение суммы ряда зависит от аргумента x.
Ряд (28.13) называется абсолютно сходящимся на множестве D, если на D сходится ряд  составленный из абсолютных значений его членов.
составленный из абсолютных значений его членов.
Всякий абсолютно сходящийсяна множестве D функциональный ряд сходится.
Признак абсолютной сходимости Д’Аламбера. Пусть для функционального ряда (28.13) существует

 (28.16)
(28.16)
Тогда:
1) в тех точках x, для которых  ряд (28.13) сходится абсолютно;
ряд (28.13) сходится абсолютно;
2) в тех точках x, для которых  ряд (28.13) расходится.
ряд (28.13) расходится.
Признак абсолютной сходимости Коши. Пусть для функционального ряда (28.13) существует

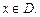 (28.17)
(28.17)
Тогда:
1) в тех точках x, для которых  ряд (28.13) сходится абсолютно;
ряд (28.13) сходится абсолютно;
2) в тех точках x, для которых  ряд (28.13) расходится.
ряд (28.13) расходится.
При  признаки Д’Аламбера и Коши не дают ответа на вопрос о сходимости или расходимости ряда. В этом случае то значение x, при котором
признаки Д’Аламбера и Коши не дают ответа на вопрос о сходимости или расходимости ряда. В этом случае то значение x, при котором  необходимо подставить в заданный функциональный ряд и исследовать полученный числовой ряд на сходимость.
необходимо подставить в заданный функциональный ряд и исследовать полученный числовой ряд на сходимость.
Ряд (28.13) называется условно сходящимся в точкеx, если в этой точке ряд сходится, но не абсолютно.
Пример 1. Найти область сходимости функционального ряда 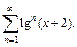
Решение. Данный ряд представляет собой сумму геометрической прогрессии:
 .
.
Он сходится и притом абсолютно, если  Из последнего условия получаем
Из последнего условия получаем

Следовательно, областью сходимости данного ряда является интервал 
Пример 2. Найти область сходимости функционального ряда 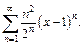
Решение. Заменяем в заданной формуле общего члена ряда 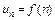 номер n на n +1 и получаем формулу следующего члена ряда
номер n на n +1 и получаем формулу следующего члена ряда  Далее, используя признакабсолютной сходимости Д’Аламбера, ищем предел:
Далее, используя признакабсолютной сходимости Д’Аламбера, ищем предел:

Определяем, при каких значениях х этот предел будет меньше единицы, т. е., решаем неравенство:
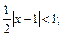

Поэтому интервал (– 1; 3) является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (– 1; 3). При  получаем знакочередующийся ряд
получаем знакочередующийся ряд 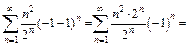
 который расходится, поскольку для него не выполняется необходимый признак сходимости:
который расходится, поскольку для него не выполняется необходимый признак сходимости: 
При 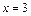 получаем знакоположительный ряд
получаем знакоположительный ряд 
 который также расходится, поскольку для него не выполняется необходимый признак сходимости.
который также расходится, поскольку для него не выполняется необходимый признак сходимости.
Следовательно, областью сходимости заданного ряда является открытый интервал (–1; 3).
Пример 3. Найти область сходимости функционального ряда 
Решение. Используя признак абсолютной сходимости Коши, ищем предел: 
Согласно признаку Коши, заданный ряд сходится при любом значении х.
Следовательно, областью сходимости заданного ряда является вся числовая ось: 
Пример 4. Найти область сходимости функционального ряда 
Решение. Нетрудно видеть, что при  ряд сходится. Пусть
ряд сходится. Пусть  Тогда для любого
Тогда для любого  имеем
имеем  Используя признак абсолютной сходимости Д’Аламбера, ищем предел:
Используя признак абсолютной сходимости Д’Аламбера, ищем предел:

Следовательно, заданный ряд сходится только при 
Задания
I уровень
1.1. Найдите область сходимости функционального ряда:
1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 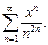
II уровень
2.1. Найдите область сходимости функционального ряда:
1) 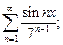 2)
2) 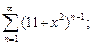 3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8) 
III уровень
3.1. Найдите область сходимости функционального ряда:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
Степенные ряды
Cтепенным рядом называется функциональный ряд вида
 (28.18)
(28.18)
где  числа
числа 
 – коэффициенты ряда.
– коэффициенты ряда.
Ряд (28.18) также называется степенным рядом с центром в точке a.
Для степенного ряда находят радиус сходимости r по одной из формул
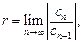
 (28.19)
(28.19)
если эти пределы существуют.
Ряд (28.18) сходится, причем абсолютно, на интервале сходимости  где
где  и расходится на
и расходится на  При
При  ряд (28.18) сходится только в точке a, при
ряд (28.18) сходится только в точке a, при  – на всей числовой оси.
– на всей числовой оси.
Для определения области сходимости заданного степенного ряда следует найти его радиус сходимости по формулам (28.19), далее определить его интервалсходимости и выяснить, сходится или расходится ряд в граничных точках этого интервала  для чего эти значения подставляют в заданный ряд и исследуют полученные числовые ряды.
для чего эти значения подставляют в заданный ряд и исследуют полученные числовые ряды.
Замечание. Поскольку степенной ряд является функциональным, то для определения области сходимости степенного ряда можно также использовать признаки абсолютной сходимости Д’Аламбера или Коши, а затем те значения x, для которых эти признаки не решают вопрос о сходимости ряда  исследуются отдельно с использованием достаточных признаков сходимости числовых рядов (см. параграф 28.3). Однако целесообразно решать эту задачу через нахождение радиуса сходимости r.
исследуются отдельно с использованием достаточных признаков сходимости числовых рядов (см. параграф 28.3). Однако целесообразно решать эту задачу через нахождение радиуса сходимости r.