Сначала рассмотрим случай, когда деформация колеса мала по сравнению с деформацией дороги (качение твердого колеса по деформируемой дороге).
Соприкосновение колеса с дорогой происходит по сложной поверхности. Каждое сечение плоскостью перпендикулярной оси вращения – это дуга окружности с центром в т.О. Элементарные нормальные реакции dz, направлены к центру О. Равнодействующая этих реакций R 
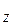, направлена туда же. Точка приложения её смещена вперед.
В каждой точке к тому же действует элементарные касательные реакции dx перпендикулярные dz. На одной части контактной поверхности элементарные реакции dx имеют проекцию в сторону движения, на другой части против движения. Т.к. они расположены под разными углами и направлены в разные стороны, то их равнодействующая R 
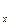не перпендикулярна R 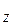, а точка приложения R 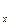расположена вне поверхности колеса. Только при буксовании или скольжении колеса R 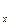перпендикулярна R .
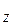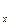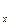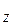Продольной реакцией R называют сумму проекций реакций R и R на плоскость дороги. Расстояние от центра колеса до вектора реакции R 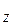называют сносом нормальной реакции.
В общем случае схема расположения сил для данного случая аналогична предыдущей. Поэтому используются те же формулы, только вместо а 
ставят а 
. Эти два рассмотренных случая являются предельными.
Далее посмотрим качение деформируемого колеса по деформируемой дороге, т.е. когда деформация дороги и колеса имеют один порядок. Тогда соприкосновение колеса с дорогой происходит по сложной поверхности, являющейся кривой переменной кривизны. В результате деформации шины радиусы кривизны участка О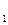 
а больше радиуса колеса. Поэтому равнодействующая R 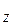пересекает линию ОО 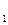в точке О 
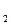выше точки О. Точка приложения реакции R 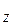смещена на расстояние а в сторону движения. Элементарные реакции dx направлены по касательной к кривой и также часть из них направлена по движению, часть направлена против движения.
|
|
Равнодействующая R 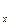расположена под углом к R 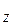. Точка приложения R 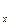расположена вне контактной поверхности. Обозначим R 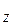как сумму проекций реакци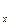й R и R 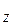на плоскость перпендикулярную дороге, а R 
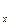как сумму проекций реакций R и R 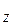на плоскость параллельную дороге. Следовательно, схема приложения сил и в этом случае аналогична, формулы остаются теми же, только вместо а 
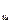ставится а.
Несмотря на то, что формулы во всех случаях одинаковы, физические процессы возникновения реакци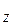й R и R различны:
В первом случае R 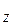равнодействующая элементарных сил упругости шины в результате её деформации, а R равнодействующая элементарных сил сцепления (трения) шины с дорогой.
Во втором случае R равнодействующая не только элементарных касательных реакций, возникающих в результате трения и сопротивления сдвигу (срезу) элементов грунта, но и проекций на плоскость дороги элементарных реакций, возникающих в результате упруго-пластической деформации грунта. А в R 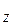входят проекции элементарных касательных реакций на плоскость перпендикулярную дороге.
В третьем (общем) случае в 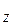R и R входят элементарные нормальные реакции, возникающий в результате упругой деформации шины, и элементарные касательные реакции, возникающие в результате взаимодействия шины с грунтом.
Знание этих процессов позволяет:
|
|
1. Определить причины потерь мощности, связанных с качением колеса.
2. Определить предельные значения R и предельные значения моментов передаваемых через колеса без буксования или скольжения.