Спектральная плотность
Пусть задан сигнал S(t), который действует в конечном интервале времени 
. Для проведения гармонического анализа поступим следующим образом:
1) Превратим наш непериодический сигнал в периодический путем повторения его с произвольным периодом Т. Для полученной таким образом функции применимо разложение в ряд Фурье:
где 
–– комплексная амплитуда n-ой гармоники.
Известно, что комплексную амплитуду можно получить из функции S(t) в соответствии с выражением (1.5):
.
2) Предположим, что Т стремится к бесконечности. В пределе получим бесконечно малые амплитуды гармонических составляющих, сумма которых изображает исходную функцию S(t). Количество этих гармоник будет бесконечно большим, а расстояние между гармониками –– бесконечно малым.
Спектр из линейчатого становится сплошным. Выразим это аналитически.
Подставим 
в S(t):
.
так как 
, то
.
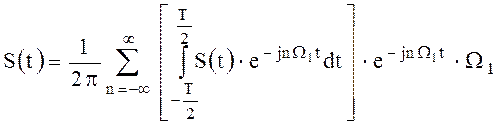При 
величина 
превращается в бесконечно малую dω; 
–– в текущую частоту 
, а операция суммирования- в операцию интегрирования, то есть 
.
Таким образом, получим:
.
В этом выражении обозначим второй интеграл через 
. (1.10)
Функция частоты 
называется спектральной плотностью или спектральной характеристикой функции времени S(t).
Подставив в исходное выражение S(t), получим:
. (1.11)
Выражения (1.10) и (1.11) носят названия пары преобразований Фурье, которые связывают между собой функцию времени S(t) и комплексную функцию частоты 
.
Поясним смысл спектральной плотности 
.
Если сигнал периодический, то n -ая гармоника с частотой 
будет иметь амплитуду 
Если же сигнал непериодический, но в некотором ограниченном интервале совпадает с периодическим S(t),то на частоте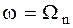 
спектральная плотность равна
.
Отсюда видно, что 
.
Так как 
.
Видно, что значение спектральной плотности на определенной частоте получается путем деления амплитуды n-ой гармоники на полосу частот 
, отделяющую соседние линии дискретного спектра. Таким образом, 
имеет смысл плотности амплитуд (амплитуда: Герц) и определяет величину сигнала, которая приходится на единицу полосы частот шириной в один Герц.
Поэтому эта непрерывная функция частоты и называется спектральной плотностью амплитуд или просто спектральной плотностью.
Огибающая сплошного спектра непериодического сигнала и огибающая линейчатого спектра периодического сигнала совпадают по форме и отличаются масштабом.
Спектральную плотность можно представить в комплексной форме:
, (1.12)
где 
.
Модуль спектральной плотности равен 
; аргумент 
.
Спектр непериодического сигнала характеризуется зависимостью модуля и аргумента спектральной плотности от частоты. В отличии от рассмотренных ранее дискретных спектров периодических колебаний, этот спектр является сплошным, так как описывается непрерывными функциями частоты 
и 
: (рисунок 1.11).
Рисунок 1.11- Зависимости модуля и аргумента спектральной плотности от частоты