Будем рассматривать детерминированные сигналы. Эти сигналы принято делить на периодические и непериодические. Сигнал является периодическим, если он удовлетворяет условию:  на интервале -
на интервале -  , где Т—период, К—целое число. Непериодический сигнал не удовлетворяет указанному условию на всей оси времени. Он задается на конечном интервале
, где Т—период, К—целое число. Непериодический сигнал не удовлетворяет указанному условию на всей оси времени. Он задается на конечном интервале  , а за пределами это интервала принимается равным нулю. В теории сигналов широко применяется спектральное представления сигналов.
, а за пределами это интервала принимается равным нулю. В теории сигналов широко применяется спектральное представления сигналов.
Спектральным представлением детерминированного сигнала S(t) называется его представление в виде суммы конечного и бесконечного числа гармонических составляющих. Основой спектрального представления сигналов является преобразование Фурье. Рассмотрим сначала спектральное представление управляющих или видеосигналов.
Ряд Фурье. Амплитудные и фазовые спектральные диаграммы
Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов.
Пусть функция S(t) периодически повторяется с частотой  и для нее выполняются условия Дирихле:
и для нее выполняются условия Дирихле:
1) в любом конечном интервале функция S(t) должна быть непрерывной или иметь конечное число разрывов первого рода, т.е. при стремление t к точкам разрыва функции S(t) должна иметь конечные пределы;
2) в пределах одного периода функция должна иметь конечное число максимумов и минимумов.
Такая периодическая функция S(t) может быть представлена в виде ряда Фурье:
 (1.1)
(1.1)
где  -среднее значение сигнала или постоянная составляющая;
-среднее значение сигнала или постоянная составляющая;
 ;
;
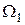 — основная частота или частота первой гармоники;
— основная частота или частота первой гармоники;
 — частоты высших гармоник.
— частоты высших гармоник.
Ряд Фурье можно записать по-другому:
 (1.2)
(1.2)
где 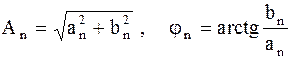 — амплитуда и начальная фаза n-ой гармоники.
— амплитуда и начальная фаза n-ой гармоники.
Обратные зависимости для коэффициентов  и
и  имеют вид:
имеют вид:
 .
.
Совокупность гармонических составляющих, на которые раскладывается функция S(t), называется спектром. Причем совокупность коэффициентов  называется спектром амплитуд, а совокупность значений
называется спектром амплитуд, а совокупность значений  называется спектром фаз.
называется спектром фаз.
Наглядное представление о спектре дают спектральные диаграммы: амплитудные (рисунок 1.4 а) и фазовые (рисунок 1.4 б). При их построении по оси абсцисс откладывают частоты гармоник, а по оси ординат –– значения амплитуд или фаз каждой гармоники.

|
Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих частотам: 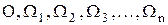 .
.
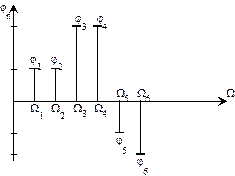
|
а б
Рисунок 1.4
Ряд Фурье можно записать и в комплексной форме. Для этого воспользуемся формулами Эйлера:
 .
.
Примем, что  . Подставляем эти соотношения в выражение (1.2), получим ряд Фурье в комплексной форме:
. Подставляем эти соотношения в выражение (1.2), получим ряд Фурье в комплексной форме:
 . (1.3)
. (1.3)
В этом выражении 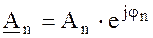 — комплексная амплитуда n-ой гармоники, которая связана с коэффициентами ряда Фурье соотношениями:
— комплексная амплитуда n-ой гармоники, которая связана с коэффициентами ряда Фурье соотношениями:
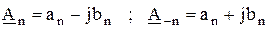 .
.
Подставляя значение  в (3), получим:
в (3), получим:
 . (1.4)
. (1.4)
Комплексную амплитуду можно получить непосредственно из функции S(t), минуя вычисление коэффициентов  и
и  .
.
 ). (1.5)
). (1.5)
Это выражение позволяет найти амплитудный спектр, то есть совокупность гармонических составляющих, в сумме образующих S(t).