Предположим теперь, что существуют две обратные матрицы А-1 И В-1. Тогда
И
Используем эти равенства для преобразования матрицы:
ЧТД
33. Базисный минор – минор, порядок которого определяет ранг матрицы.
Ранг матрицы - это наибольший из порядков ее миноров(отличных от нуля) и максимальное число линейно независимых строк (не нулевых стррок)
Элементарными называются следующие преобразования матрицы:
Перестановка двух любых строк (или столбцов),
Умножение строки (или столбца) на отличное от нуля число,
Прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,
34. Транспонированная матрица — матрица полученная из исходной матрицы A заменой строк на
Столбцы
Свойства:
35. Система линейных алгебраических уравнений — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.
Если система уравнений имеет хотя бы одно решение, то она называется совместной.
Если система уравнений решений не имеет, то она называется несовместной.
Если СЛАУ имеет единственное решение, то ее называют определенной;
если решений больше одного, то – неопределенной.
Если свободные члены всех уравнений системы равны нулю, то система называется однородной, в противном случае – неоднородн
Метод гаусса:
Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на 1/2):
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
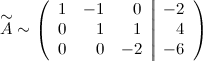От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на -1/2, получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент, для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
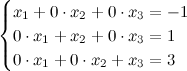Полученной матрице соответствует система
Ответ:
36. Теорема о совместности однородной системы линейных уравнений.
Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т.е r<n
Необходимость.
Т.к ранг не может превосходить размера матрицы, то, очевидно, r< или = n. Пусть r=n. Тогда один из миноров размера n x n отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: xi= ∆i/∆=0, ∆i=0, ∆ не =0. Значит, других, кроме тривиальных, решений нет. Если есть нетривиальное решение, то r<n.
Достаточность.
Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е имеет и ненулевые решения.
Однородная система всегда совместна,она имеет нулевое(тривиальное) решение х1=х2=….=хn=0
37. Теоре́ма Кро́некера — Капе́лли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы
Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
38. 
Решение квадратной системы лин урав при помощи обратной матрицы
Где
Обратную матрицу найдем по формуле:
Сначала разбираемся с определителем:
Внимание! Если определитель А=0, то обратной матрицы не существует, и решить систему матричным методом невозможно.
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
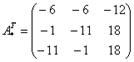Итд
Таким образом:
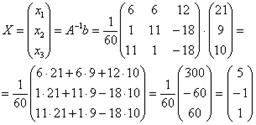
39. Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение,
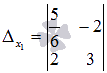Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители дельта х1 и дельта х2. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель
Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем
Вычисляем эти определители:
Находим неизвестные переменные x1 и x2 по формулам
получаем
40. Ве́кторное (или лине́йное) простра́нство — математическая структура, которая представляет собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр
Линейное подпространство или векторное подпространство ― непустое подмножество {\displaystyle K} K линейного пространства {\displaystyle V} V такое, что {\displaystyle K} K само является линейным пространством по отношению к определенным в {\displaystyle V} V действиям сложения и умножения на скаляр
41. Линейное(векторное) пространство. Пространство Rⁿ и линейные операции в этом пространстве.
Векторное (линейное) пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства.
Векторным пространством (над полем R или C) называют множество L, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные (комплексные) числа, удовлетворяющие следующим условиям:
1) x + y = y + x (коммутативность сложения);
2) (x + y) + z = x + (y + z) (ассоциативность сложения);
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x для любого вектора x;
4) для любого вектора x существует противоположный ему вектор y такой, что x + y = 0;
5) 1∙x = x;
6) α(βx) = (αβ)x (ассоциативность умножения);
7) (α + β)x = αx + βx (дистрибутивность относительно числового множителя);
8) α(x + y) = αx + αy (дистрибутивность относительно векторного множителя).
Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2,...en, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e1, e2,...en - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:
x = α1e1 + α2e2 +... + αnen.
При этом числа α1, α2,...,αn называют координатами вектора x в данном базисе.
Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2,..., λn). Сумма двух векторов и произведение на число определяются соотношениями:
(λ1, λ2,..., λn) + (μ1, μ2,..., μn) =
= (λ1 + μ1, λ2 + μ2,..., λn + μn),
α∙(λ1, λ2,..., λn) = (α∙λ1, α∙λ2,..., α∙λn).
Базисом в этом пространстве может служить, например, следующая система из n векторов: e1 = (1, 0,..., 0), e2 = (0, 1,..., 0),...en = (0, 0,..., 1).
42. Базис линейного пространства. Примеры базисов в R в степени n.
Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1) система линейно независима.
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов)
Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора, взятые в определённом порядке. Эти векторы называются базисными.
43. ТЕОРЕМА (О разложении вектора по базису). Любой вектор некоторого пространства можно разложить по его базису, причем такое разложение единственно
Таким образом, чтобы разложить некоторый вектор {a} по базису е1 е2 еn необходимо найти такие коэффициенты a1 a2 an при которых линейная комбинация базисных векторов e1 e2 en равны вектору а
44. Критерий линейной зависимости векторов в пространстве Rⁿ
система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная
Критерий линейной зависимости векторов: Для того чтобы векторы х1 х2 хr (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
45. Евклидовым пространством размерности n называется n-мерное линейное пространство над полем вещественных чисел, в котором каждой паре векторов x y поставлено в соответствие вещественное число, обозначаемое через (x:y) и называемое скалярным произведением этих векторов
46. 
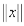Линейное пространство L называется нормированным, если любому его элементу x поставлено в соответствие число, называемое нормой и обозначаемое, причем при этом выполнены следующие условия:
47. Собственные числа и собственные векторы квадратной матрицы. Их св-ва.
Определение: ненулевой вектор х, который при умножении на некоторую квадратную матрицу а превращается в самого же себя с числовым коэффициентом лямда, называется собственным вектором матрицы а. Число лямда называют собственным значением или собственным числом данной матрицы.
Св-ва: 1) Собственные векторы, соответствующие различным собственным значениям, линейно
независимы.
2) Если матрица оператора симметричная, т.е. аij=аji, всякий i, j =1, 2,..., n, то собственные
значения ее вещественные.
3) Если собственные векторы матрицы образуют базис, то в этом базисе матрица оператора
имеет диагональный вид, причем ее диагональными элементами являются собственные числа.
Характеристическое уравнение 
48. Линейная балансовая модель.
Пусть рассматривается экономическая система, состоящая из n
взаимосвязанных отраслей производства. Продукция каждой отрасли частично
идет на внешнее потребление (конечный продукт), а частично используется в
качестве сырья, полуфабрикатов или других средств производства в других
отраслях, в том числе и в данной. Эту часть продукции называют
производственным потреблением. Поэтому каждая из рассматриваемых отраслей
выступает и как производитель продукции (первый столбец таблицы 1) и как
ее потребитель (первая строка таблицы 1).
Обозначим через xi валовый выпуск продукции i-й отрасли за
планируемый период и через yi – конечный продукт, идущий на внешнее для
рассматриваемой системы потребление (средства производства других
экономических систем, потребление населения, образование запасов и т.д.).
Таким образом, разность xi - yi составляет часть продукции i-й
отрасли, предназначенную для внутрипроизводственного потребления. Будем в
дальнейшем полагать, что баланс составляется не в натуральном, а в
стоимостном разрезе.
Одна из задач балансовых исследований заключается в том, чтобы на
базе данных об исполнение баланса за предшествующий период определить
исходные данные на планируемый период.
49. Модель международной торговли
Эта модель служит основным теоретическим инструментом анализа международной торговли. Модель оперирует совокупным спросом и предложением и исходит из предпосылки о существовании торговли двумя товарами между двумя странами.
В рамках стандартной модели рассматривается и производство товаров с растущими издержками замещения.
Простейший случай обмена товаров. В стандартной модели обмен товаров принято задавать прямой линией, что соответствует идее линейного (пропорционального) обмена. Рисунок 8.1 иллюстрирует случай, когда некая страна, обладая количеством Ь товара В, желает обменивать его на некоторое количество а товара А. «Условия торговли», т.е. соотношение обмена товара В на товар А, задаются прямой ab (линией обмена товаров). Другими словами, обмен задается одним и тем же коэффициентом пропорциональности (к = tga). Функция предпочтения между товарами А и В как обычно выражена графически кривыми безразличия, позволяющими точно оценить степень предпочтительности того или иного набора благ (товаров А и В), а также определить по этому признаку различные комбинации двух товаров. При анализе влияния международной торговли на общественное благосостояние используют кривые безразличия, отражающие вкусы и предпочтения страны в целом, или так называемые общественные кривые безразличия. При переходе от индивидуальных кривых
безразличия к общественным делается необходимое предположение о том, ЧТО каждый потребитель имеет одни и те же вкусы и предпочтения и наделен одними и теми же факторами производства.
Кривые безразличия U0, U1, U1 на рис. 8.1 показывают, каким количеством единиц одного товара общество готово пожертвовать, чтобы получить дополнительную единицу другого товара и при том чтобы благосостояние общества оставалось на прежнем уровне.
50.. Линейные операторы. Основные понятия.
Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
51. Взаимно однозначные отображения
Взаимно однозначным соответствием между множествами X и Y (или отображением X на Y) называется соответствие (соответственно, отображение), обладающее следующими тремя свойствами:
1) каждому элементу множества X соответствует один и только один элемент множества Y;
2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y;
3) всякий элемент множества Y соответствует хотя бы одному элементу множества X.
52. Запись числа z в виде z=x+iy называют алгебраической формой комплексного числа.
Суммой двух комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством:
z1+z2=(x1+x2)+i(y1+y2)
Вычитание комплексных чисел.
Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:
Z=z1-z2=(x1-x2)+i(y1-y2)
Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством:
Z=z1z2=(x1x2-y1y2)+i(x1y2+y1x2)
Отсюда, в частности, следует важнейшее соотношение:
i²=-1