Дисперсия представляет собой среднюю арифметическую из квадратов отклонений вариант от их средней арифметической
σ2 = ∑ (xi - x0)2 * f / ∑f
Сгруппируем рабочих по разрядам, построив дискретный ряд распределения:
Цех №1:
Таблица 3.1
| Разряд (x) | Число рабочих (f) |
| Итого |
Средний разряд по цеху №1 находим по средней взвешенной:
(1*7+2*13+3*10+4*6+5*3+6*1)/40= 2,7

Группировку рабочих Цеха №2 проводили в таблице 2

Определим коэффициенты вариации рабочих по цехам:
V = σ / x * 100%
где: σ - среднее квадратическое отклонение;
x - средний разряд.
σ = √ σ2
σц1 = √ 1,61 = 1,27;
σц2 = √ 1,49 = 1,22;
Для цеха №1: (1,27/2,7)*100%= 47,04%
Для цеха №2: (1,22/3,2)*100%= 38%
Коэффициент вариации является критерием надежности средней. Различие указывает на большую колеблемость в величине тарифных разрядов у рабочих 1-го цеха. Тарифный разряд рабочих второго цеха имеет более низкий коэффициент, а следовательно более высокую степень однородности тарифного разряда рабочих цеха.
Задача 4. С вероятностью 0,954 определить ошибку выборки для среднего тарифного разряда рабочих завода и для доли рабочих, имеющих четвертый разряд. Указать пределы возможных значений этих показателей в генеральной совокупности
Выборочным называется такое наблюдение, при котором характеристика всей совокупности единиц дается по некоторой ее части, отобранной в случайном порядке. Выборочное наблюдение - наиболее распространенный вид несплошного наблюдения. Оно дает возможность, не прибегая к сплошному наблюдению, получить обобщающие показатели, которые правильно отражают характеристики всей совокупности в целом.
Вся совокупность единиц называется генеральной совокупностью, а та часть совокупности единиц, которая подвергается выборочному обследованию, называется выборочной совокупностью. Задача выборочного наблюдения - получить правильное представление о показателях генеральной совокупности на основе изучения выборочной совокупности.
Основными вопросами теории выборочного наблюдения являются:
определение предельной ошибки выборки для различных типов выборочных характеристик с учетом особенностей отбора;
определение объема выборки, обеспечивающего необходимую репрезентативность выборочной совокупности с учетом особенностей отбора.
Величина предельной ошибки выборки зависит от вариации признака внутри совокупности объема выборки. И способа отбора единиц.
Определим ошибку выборки для среднего тарифного разряда рабочих завода:
Средний тарифный разряд рабочих завода является:
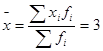
Дисперсия по заводу:
 .
.
Предельная ошибка выборки определяется по формуле:
 ,
,
Где: 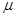 - средняя ошибка выборки;
- средняя ошибка выборки;
t - коэффициент доверия, зависящий от вероятности ( ), с которой можно утверждать, что предельная ошибка не превысит t - кратное значение средней ошибки.
), с которой можно утверждать, что предельная ошибка не превысит t - кратное значение средней ошибки.
При  = 0,954 t = 2,0
= 0,954 t = 2,0
 = 10% = 0,1 (исх. данные)
= 10% = 0,1 (исх. данные)
Т.е. объем выборочной совокупности (n) 100 человек, а объем генеральной совокупности (N) 1000 человек. Исходя из условий задания, отбор бесповторный.
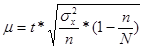
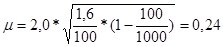 - средняя ошибка для среднего тарифного разряда
- средняя ошибка для среднего тарифного разряда
Тогда предельная ошибка для среднего тарифного разряда равна:

 = 3
= 3
 -
- 






Ошибка выборки по среднему тарифному разряду равна 0,48.
Тогда средний тарифный разряд рабочих завода колеблется от 2,52 до 3,48.
Определим ошибку выборки для доли рабочих имеющих 4 разряд.
Рассчитаем ошибку выборки по альтернативному признаку:
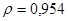
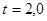





Определим среднее значение альтернативного показателя: из 100 человек 20 имеют 4 разряд.

Определим среднюю ошибку для доли рабочих, имеющих 4 разряд.
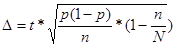




Ошибка выборки для рабочих завода имеющих 4 разряд составляет 0,076.
Доля рабочих, имеющих 4 разряд, колеблется от 0,124 до 0,276.