Интегральные преобразования
Операционное исчисление и некоторые его приложения
Пусть задана функция действительного переменного t, которая удовлетворяет условиям:
1) 
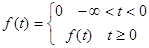
2) Функция f(t) кусочно-непрерывная (имеет конечное число точек разрыва первого рода).
3) Для любого значения параметра t>0 существует M>0 и S0³0 такие, что выполняется условие: |f(t)|<Me S0t
Рассмотрим функцию f(t)×e-pt, где р – комплексное число р = (а + i b).
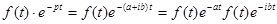(1)
Применим к этому соотношению формулу Эйлера:
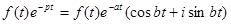
Проинтегрировав это равенство получим:
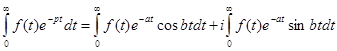(2)
Оценим левую часть равенства (2):
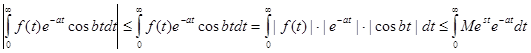
А согласно свойству (3) |f(t)| < Me S0t
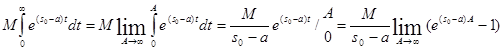
В случае если a>S0 имеем:
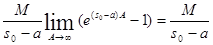
Аналогично можно доказать, что существует и сходится второй интеграл в равенстве (2).
Таким образом при a>S0 интеграл, стоящий в левой части равенства (2) также существует и сходится. Этот интеграл определяет собой функцию от комплексного параметра р:
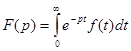(3)
Функция F(p) называется изображением функции f(t) по Лапласу, а функция f(t) по отношению к F(p) называется оригиналом.
f(t) Ü F(p), где F(p) – изображение функции f(t) по Лапласу.
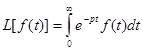- это оператор Лапласа.
Смысл введения интегральных преобразований.
Этот смысл состоит в следующем: с помощью перехода в область изображения удается упростить решение многих задач, в частности свести задачу решения многих задач дифференциального, интегрального и интегро-дифференциального уравнения к решению алгебраических уравнений.
Теорема единственности: если две функции j(t) и Y(t) имеют одно и то же изображение F(p), то эти функции тождественно равны.
Смысл теоремы: если при решении задачи мы определим изображение искомой функции, а затем по изображению нашли оригинал, то на основании теоремы единственности можно утверждать, что найденная функция является решением в области оригинала и причем единственным.
Изображение функций s0(t), sin (t), cos (t).
Определение: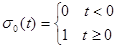 
называется единичной функцией.
Единичная функция удовлетворяет требованиям, которые должны быть наложены на функцию для существования изображения по Лапласу. Найдем это изображение:
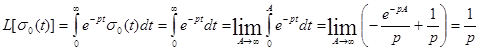
Изображение единичной функции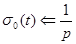 
Рассуждая аналогичным образом получим изображение для функции sin(t):
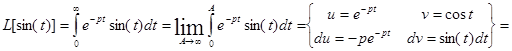
интегрируя по частям получим:
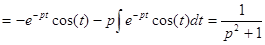т.е.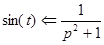 
Аналогично можно доказать, что cos (t) переходит в функцию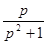 
в области преобразований. Откуда: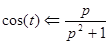 
Изображение функции с измененным масштабом независимого переменного.
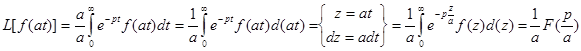где а – константа.
Таким образом: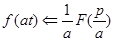 
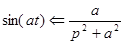и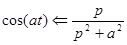 
Свойства линейности изображения.
Теорема: изображение суммы нескольких функций умноженное на постоянные равны сумме изображений этих функций умноженных на те же постоянные.
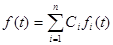
Если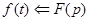 
, то 
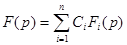, где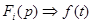 
Теорема смещения: если функция F(p) это изображение f(t), то F(a+p) является изображением функции e-at f(t) (4)
Доказательство:
Применим оператор Лапласа к левой части равенства (4)
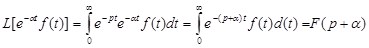
Что и требовалось доказать.
Таблица основных изображений:
| F(p) | f(t) | F(p) | f(p) |
| 
| 
| |
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
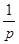
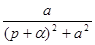
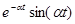
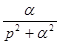
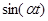
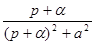
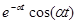
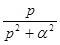
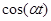
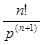
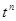
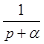
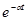
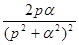
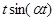
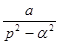
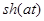
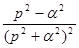
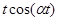
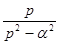
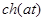
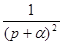
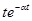
Изображение производных.
Теорема. Если 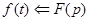, то справедливо выражение:
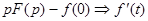(1)
Доказательство:
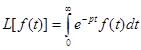
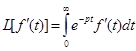
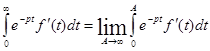(2)
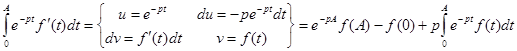(3)
Подставляя (3) в (2) и учитывая третье условие существования функции Лапласа имеем:
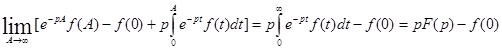
Что и требовалось доказать.
Пример: Решить дифференциальное уравнение:
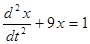Если x (0)=0 и x ’(0)=0
Предположим, что x (t) – решение в области оригиналов и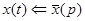 
, где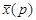 
- решение в области изображений.
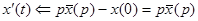
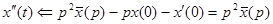
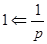
Изображающее уравнение:
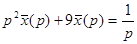
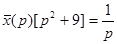
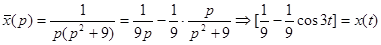
Теорема о интегрировании оригинала. Пусть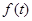 
находится в области оригиналов, 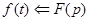, тогда 
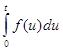также оригинал, а его изображение 
.
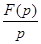Таким образом операции интегрирования в области оригиналов соответствует операция деления в области изображений.
Теорема о интегрировании изображений: Пусть 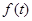– функция оригинал, которая имеет изображение 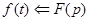и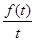 
также оригинал, а 
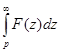- является сходящимся интегралом, тогда 
.
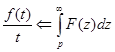Толкование теоремы: операция деления на аргумент в области оригиналов соответствует операции интегрирования в пределах от р до ¥ в области изображений.