Преобразование Лапласа имеет вид:
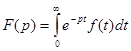(1)
На f(t) наложены условия:
1) f(t) определена и непрерывна на всем интервале: (-¥; ¥)
2) f(t) º 0, t Î (- ¥;0)
3) При M, S0 >0, для всех t > 0 выполняется условие |f(t)|<Me S0t
Если отказаться от условий 2 и 3, и считать, что f(t) принимает произвольное значение при t < 0, то вместо (1) можно рассмотреть следующий интеграл:
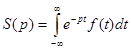(2)
Формула (2) – двустороннее преобразование Лапласа.
Пусть в (1) и (2) p =a + in, где a и n – действительные числа.
Предположим, что Re (p) = a = 0, т.е.
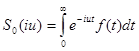(4)
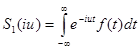(5)
(4) и (5) соответственно односторонние и двусторонние преобразования Фурье.
Для существования преобразования Фурье, функция должна удовлетворять условиям:
1) Должна быть определена на промежутке (-¥; ¥), непрерывна всюду, за исключением конечного числа точек разрыва первого рода.
2) Любой конечный промежуток оси t можно разделить на конечное число промежутков, в каждом из которых функция либо кусочно-гладкая, либо кусочно-монотонная.
3) Функция абсолютно интегрируема: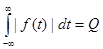 
, это условие выполняется, если |f(t)|<Me S0t
Из существования преобразования Лапласа не следует преобразование Фурье. Преобразования Фурье существуют для более узкого класса функций. Преобразования Фурье не существуют для постоянной и ограниченной функции: f(t) = C
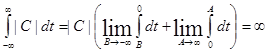
Аналогично преобразования Фурье не существуют и для гармоничных функций:
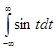т.к.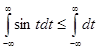 
Если f(t) = 0 при t>0 и преобразование для этой функции существует, то оно может быть получено из таблицы оригиналов и изображений для преобразования Лапласа путем замены параметра t на iu, но при этом необходимо убедиться, что F(p) не обращается в число справа от мнимой оси.
Если f(t) ¹ 0, t<0
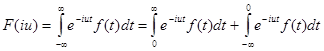(6)
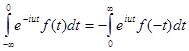
Обозначим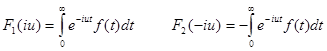 
Очевидно, что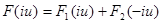 
(6’)
Функция (6) называется спектральной плотностью
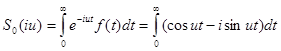
В связи с изложенным можно указать два пути отыскания спектральной плотности:
1) Вычисление интеграла (5)
2) Использование преобразования Лапласа или Фурье.
Непосредственное вычисление спектральной плотности для абсолютно интегрируемой функции.
Функция F(iu) может быть представлена, как комплексная функция действительной переменной
(7)
| F(iu)| - амплитудное значение спектральной плотности, y (u) – фазовый угол.
В алгебраической форме: F(iu) = a(u) +ib(u)
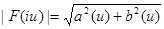(8)
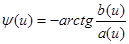(9)
Для непосредственного вычисления спектральной плотности вычисляется интеграл (6), а затем по формулам (8) и (9) определяется амплитудное значение | F(iu)| и фазовый угол y (u).
Пример.
Найти спектральную плотность импульса: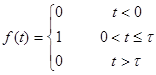 
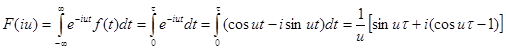
откуда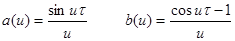 
, далее
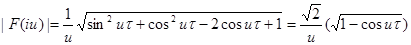
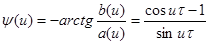
Отыскание спектральной плотности для неабсолютно интегрируемых функций.
Прямое преобразование Фурье для таких функций не существует, существует преобразование Лагранжа.
Прямое преобразование Фурье необходимо:
1) Для облегчения процесса решения дифференциальных и интегральных уравнений.
2) Для исследования амплитудной и частотной характеристик спектральной плотности, определенной всюду на числовой оси.
Введем следующее определение спектральной плотности для неабсолютно интегрируемых функций:
Если для заданной функции y=f(t) существует непрерывное изображение по Лапласу F(p), то спектральной плотностью функции называется изображение функции по Лапласу при p = iu.
Спектральной плотностью F1(iu) неабсолютно интегрируемой функции называется предел от спектральной плотности F2(iua) абсолютно интегрируемой функции.
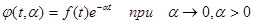
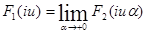
Список литературы
Для подготовки данной работы были использованы материалы с сайта https://www.ed.vseved.ru/