Обработка ведомости вычисления вершин теодолитного хода.
Для заполнения таблицы 4 необходимо выполнить расчеты в графах 4, 5, 7, 8, 9, 10, 11, 12. Данные в остальных графах, а также координаты точки I являются общими для всех вариантов.
Вычисление дирекционных углов и румбов сторон хода.
По исходному дирекционному углу αI-II и исправленным значениям измеренных углов ß хода вычисляют дирекционные углы всех остальных сторон хода: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный угол хода, образованный этими сторонами.
Пример:
α II-III = α I-II + 180° - ßII = 183° 27´ + 180° - 90° 42.9´ = 272° 44.1´
Для контроля вычисления дирекционных углов следует найти дирекционный угол стороны I-II через дирекционный угол стороны V-I и исправленный угол ßV. Он должен совпасть с углом, записанным в первой строчке графы 4 ведомости.
Далее необходимо перевести дирекционные углы в румбы. Дирекционные углы в румбы переводились в задаче 2.
Вычисленные значения румбов записывают в графу 5 ведомости, при этом значения румбов округляют до целых минут.
Вычисление приращений координат.
Приращения вычисляют по формулам, также, как в задаче 2 задания 1:
ΔX = d cos α
ΔY = d sin α
Где d – длина линии (горизонтальное проложение), а α – дирекционный угол этой линии.
Вычисленные значения приращений ΔX и ΔY записывают в графы 7 и 8 ведомости с точностью до сотых долей метра. В каждой из граф складывают все вычисленные значения ΔX и ΔY и находят практические суммы приращений координат - ∑ΔXпр и ∑ΔYпр.
Нахождение абсолютной и относительной линейных невязок хода; увязка приращений координат.
Невязка (ƒx и ƒy) – это расхождение между теоретической суммой приращений и той, которую получили в результате вычислений. Эта погрешность возникает в результате неточности измерений горизонтальных углов и проложений.
Сначала вычисляют невязки ƒx и ƒy в приращениях координат по осям X и Y по формулам:
ƒx = ∑ΔXпр -∑ΔXт
ƒy = ∑ΔYпр - ∑ΔYт
Примечание:
Для разомкнутого хода ∑ΔXт и ∑ΔYт вычисляются как разности абсцисс и ординат (т.е. разность координат) конечной и начальной точек хода.
Для замкнутого хода ∑ΔXт и ∑ΔYт всегда равны нулю.
Абсолютную линейную невязку ΔΡ хода вычисляют по формуле:
ΔΡ = 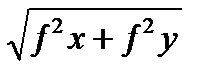 и записывают с точностью до сотых долей метра.
и записывают с точностью до сотых долей метра.
Относительная линейная невязка  хода (P – сумма длин сторон хода). Если относительная невязка окажется меньше допустимой 1/2000, то невязки ƒx и ƒy распределяют, вводя поправки в вычисленные значения приращений координат. Поправки в приращения распределяют прямо пропорционально длинам сторон хода, записанным в графе 6 (если эти длины примерно одинаковы, то поправки можно распределить поровну). Поправки вводят со знаком, обратным знаку невязки.
хода (P – сумма длин сторон хода). Если относительная невязка окажется меньше допустимой 1/2000, то невязки ƒx и ƒy распределяют, вводя поправки в вычисленные значения приращений координат. Поправки в приращения распределяют прямо пропорционально длинам сторон хода, записанным в графе 6 (если эти длины примерно одинаковы, то поправки можно распределить поровну). Поправки вводят со знаком, обратным знаку невязки.
Вычисление координат вершин хода.
Координаты вершин хода получают путём последовательного алгебраического сложения координат предыдущих вершин хода с соответствующими исправленными приращениями:
XII = XI + ΔXI-II; XIII = XII + ΔXII-III и т.д.
Контролем правильности является получение координат точки I в конце вычислений.
Таблица 4 -Ведомость вычисления координат вершин теодолитного хода
| № вершин хода | Измеренные углы | Исправленные углы | Дирекционные углы | Румбы | Длины линий (гориз. Пролож.) d | Приращение координат, м | Координаты | № вершин хода | ||||||||||||||||
| Вычисленные | Исправленные | |||||||||||||||||||||||
| ° | ´ | ° | ´ | ° | ´ | Назв | ° | ´ | ± | Δx | ± | Δy | ± | Δx | ± | Δy | ± | x | ± | y | ||||
| I | ЮЗ | 34,13 | - | -1 34,07 | - | +1 2,05 | - | 34,08 | - | 2,04 | + | 1925,75 | + | 2321,11 | I | |||||||||
| II | 42,9 | 43,2 | + | 1891,67 | + | 2319,07 | II | |||||||||||||||||
| 43,8 | СЗ | 16,2 | 37,83 | + | -1 1,80 | - | +2 37,79 | + | 1,79 | - | 37,77 | |||||||||||||
| III | 67,4 | 57,7 | + | 1893,46 | + | 2281,30 | III | |||||||||||||||||
| 46,1 | СЗ | 13,9 | 30,35 | + | -1 30,22 | - | +1 2,77 | + | 30,21 | - | 2,76 | |||||||||||||
| IV | 27,6 | 27,9 | + | 1923,67 | + | 2278,54 | IV | |||||||||||||||||
| 18,2 | СВ | 18,2 | 34,90 | + | -1 27,39 | + | +1 21,63 | + | 27,38 | + | 21,64 | |||||||||||||
| V | 54,3 | + | 1951,05 | + | 2300,18 | V | ||||||||||||||||||
| 23,9 | ЮВ | 36,1 | 32,82 | - | -1 25,29 | + | +1 20,92 | - | 25,30 | + | 20,93 | |||||||||||||
| I | 56,6 | 56,9 | + | 1925,75 | + | 2321,11 | I | |||||||||||||||||
| ∑ßт = 180°×(n-2) | P=170,03 | + | 59,41 | + | 42,55 | + | 59,38 | + | 42,59 | |||||||||||||||
| ∑ßпр | 58,5 | |||||||||||||||||||||||
| - | 59,36 | - | 42,61 | - | 59,38 | - | 42,59 | |||||||||||||||||
| ∑ßт | ||||||||||||||||||||||||
| ƒ | + | 0,05 | - | 0,06 | ||||||||||||||||||||
| ħ | +0 | 01,5 | 00,0 | |||||||||||||||||||||
| ∑∆пр | ΔΡ=  = =  ; ; 

| |||||||||||||||||||||||
Доп. ƒß = ±1´  = ±1´ = ±1´ 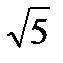 = ±0° 02,2´ = ±0° 02,2´
| ||||||||||||||||||||||||
| Доп. ƒß | ±0 | 02,2 | ||||||||||||||||||||||