 Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.
Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.




 1. Пусть даны а = (ах, аy, аz) и в = (вx, ву, вz), тогда сумма этих векторов есть вектор с, координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (ах + вx; аy + ву; аz + вz).
1. Пусть даны а = (ах, аy, аz) и в = (вx, ву, вz), тогда сумма этих векторов есть вектор с, координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (ах + вx; аy + ву; аz + вz).

 Пример 1.
Пример 1.
 а = (3; 4; 6) и в = (-1; 4; -3), тогда с = (3 + (-1); 4 + 4; 6 + (-3)) = (2; 8; 3).
а = (3; 4; 6) и в = (-1; 4; -3), тогда с = (3 + (-1); 4 + 4; 6 + (-3)) = (2; 8; 3).





 2. а = (ах, аy, аz) и в = (вx, ву, вz), тогда разность этих векторов есть вектор с, координаты которого равны разности одноименных координат данных векторов, т.е. с = а - в = (ах - вx; аy - ву; аz - вz).
2. а = (ах, аy, аz) и в = (вx, ву, вz), тогда разность этих векторов есть вектор с, координаты которого равны разности одноименных координат данных векторов, т.е. с = а - в = (ах - вx; аy - ву; аz - вz).
Пример 2.




 а = (-2; 8; -3) и в = (-4; -5; 0), тогда с = а – в = (-2 – (-4); 8 – (-5); -3 –0) = (2; -13; -3).
а = (-2; 8; -3) и в = (-4; -5; 0), тогда с = а – в = (-2 – (-4); 8 – (-5); -3 –0) = (2; -13; -3).
 3. При умножении вектора а = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. ма = (мах, маy, маz).
3. При умножении вектора а = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. ма = (мах, маy, маz).
 Пример 3.
Пример 3.
 а = (-8; 4; 0) и м = 3, тогда 3 а = (-8 х 3; 4 х 3; 0 х 3) = (-24; 12; 0).
а = (-8; 4; 0) и м = 3, тогда 3 а = (-8 х 3; 4 х 3; 0 х 3) = (-24; 12; 0).
Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач.
Рассмотрим доказательство некоторых теорем с помощью векторов.
Теорема 1.
Диагонали ромба взаимно перпендикулярны.
Доказательство.













 Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в. Из определения ромба: АВ = DC = а, AD = ВС = в.
Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в. Из определения ромба: АВ = DC = а, AD = ВС = в.




 По определению суммы и разности векторов АС = а + в; DВ = а – в.
По определению суммы и разности векторов АС = а + в; DВ = а – в.


 Рассмотрим АС * DВ = (а + в)(а – в) = а2 – в2.
Рассмотрим АС * DВ = (а + в)(а – в) = а2 – в2.
 |


 Так как стороны ромба равны, то а = в. Следовательно, AC * DB =0. Из последнего получаем
Так как стороны ромба равны, то а = в. Следовательно, AC * DB =0. Из последнего получаем
Ч.т.д.
Рассмотрим теперь решение задач с помощью векторов.
Задача 1.

 Даны два вектора AB и CD, причем А(-1; 2; 4), В (-4; 5; 4), С(-1; -2; 2) и D(2; 1;5).
Даны два вектора AB и CD, причем А(-1; 2; 4), В (-4; 5; 4), С(-1; -2; 2) и D(2; 1;5).
Определить, перпендикулярны они друг другу или нет.
Решение.

 Найдем сначала координаты векторов. АВ = (-3; 3; 0) и СD = (3; 3; 3).
Найдем сначала координаты векторов. АВ = (-3; 3; 0) и СD = (3; 3; 3).


 Вычислим теперь скалярное произведение этих векторов:
Вычислим теперь скалярное произведение этих векторов:
АВ х СD = (-3) х 3 + 3 х 3 + 0 х 3 = 0.

 Последнее и означает, что АВ СD.
Последнее и означает, что АВ СD.
Задача 2.
Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.

Решение.
Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с:


 ВС = а, СА = в, АВ = с
ВС = а, СА = в, АВ = с
(рис.8). Тогда




 АD = АВ + ВD = АВ +
АD = АВ + ВD = АВ +  = с +
= с + 
аналогично определяются и другие медианы:

 ВЕ = а +
ВЕ = а + 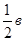 , СF = в +
, СF = в + 


 Так как, в силу условия замкнутости
Так как, в силу условия замкнутости
ВС + СА + АВ = а + в + с = 0,
то мы имеем:




 АD + ВЕ + СF = (с +
АD + ВЕ + СF = (с +  ) + (а +
) + (а + 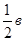 ) + (в +
) + (в +  ) =
) =  (а + в + с) =
(а + в + с) = 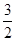 х 0 = 0.
х 0 = 0.






 Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор С1D1 = СF, мы получим.
Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор С1D1 = СF, мы получим.
 А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 3.
Доказать, что для любого треугольника имеет место формула
с2 = а2 + в2 – 2ав х соs С (теорема косинусов)


 Решение.
Решение.
 Положим: а = СВ, в = СА,
Положим: а = СВ, в = СА,
с = АВ (рис.10).
Тогда с = а – в, и мы имеем
(учитывая, что угол между векторами а и в равен С):
с2 = (а – в)2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2.
Задача 4.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Решение.
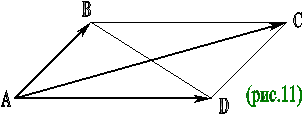
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства





 АВ + AD = АС, АВ – АD = DВ.
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:









 АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
Задача 5.

 Даны три точки: А (1; 1), В (-1; 0), С (0; 1). найдите такую точку D (х; y), чтобы векторы АВ и СD были равны.
Даны три точки: А (1; 1), В (-1; 0), С (0; 1). найдите такую точку D (х; y), чтобы векторы АВ и СD были равны.
Решение.



 Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y – 1. Так как АВ = СD, то х – 0 = -2, y – 1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y – 1. Так как АВ = СD, то х – 0 = -2, y – 1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Задача 6.

 Даны два вектора АВ и СD, причем А (-1; 2; 4), В (-4; 5; 4), С (-1; -2; 2), D (2; 1; 5).Определить, перпендикулярны они друг другу или нет.
Даны два вектора АВ и СD, причем А (-1; 2; 4), В (-4; 5; 4), С (-1; -2; 2), D (2; 1; 5).Определить, перпендикулярны они друг другу или нет.

 Решение.
Решение.
Найдем сначала координаты векторов. АВ = (-3; 3; 0) и СD (3; 3; 3).

 Вычислим теперь скалярное произведение этих векторов:
Вычислим теперь скалярное произведение этих векторов:

 AB х CD = (-3) х 3 + 3 х 3 + 0 х 3 = 0.
AB х CD = (-3) х 3 + 3 х 3 + 0 х 3 = 0.
 Последнее озночает, что АВ СD.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является весьма мощных средством решения геометрических и многих физических (и технических) задач.
Используемая литература.
1. “Векторы в школьном курсе геометрии”. (1976г.) В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.
2. “Векторы в курсе геометрии средней школы. (1962г.) В.Г.Болтянский. И.М.Яглом.