Механизм получения уравнений описывающих поля в реальных средах состоит из 2 этапов: 1 – формулируется закон сохранения. на 2 – этот закон до определяется уравнениями состояния связывающими между собой величины. Законы сохранения выражают факт многообразия носят экспериментальный характер. Эти уравнения называются уравнения состояния. Именно в них сконцентрировано основная масса допущений и предположений о свойстве среды и характер рассматриваемого процесса. Свобода в выборе состояния приводит к модификациям уравнений описывающих один и тот же тип физического поля. Другие источники погрешности построения уравнения теории поля состоят в неполноте используемых законов.
Общая форма записи такова
+ div 
= gj
ρj – плотность заряда соответствующей величины
Jj – плотность тока этой величины ρj - Jj
gj – плотность внешнего притока внутренних источников.
Это уравнение формулируется так
Изменение плотности некоторой величины в данной точке складывается из расходимости плотности её тока и внутренних источников её величины
БИЛЕТ 11 (11, 31, 51)
Тензор деформации.
Те́нзор деформа́ции — тензор, который характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации.
Тензор деформации Коши-Грина в классической сплошной среде (частицы которой являются материальными точками и обладают лишь тремя трансляционными степенями свободы) определяется как
Где 
— вектор, описывающий смещение точки тела: его координаты — разность между координатами близких точек после 
и до 
деформации. Дифференцирование производится по координатам в отсчетной конфигурации (до деформирования). Расстояния до и после деформации связаны через 
по повторяющимся индексам ведётся суммирование).
По определению тензор деформации симметричен, то есть 
В некоторых источниках этот тензор деформации называют тензором деформации Грина-Лагранжа, а правую меру деформации Коши-Грина (удвоенный обсуждаемый тензор деформации плюс единичный тензор) — правым тензором деформации Коши-Грина.
Нелинейный тензор деформации Коши-Грина обладает свойством материальной объективности. Это означает, что если кусок деформируемого тела совершает жесткое движение, тензор деформации поворачивается вместе с элементарным объемом материала. Удобно использовать такие тензоры при записи определяющих уравнений материала, тогда принцип материальной объективности выполняется автоматически, то есть если наблюдатель двигается относительно деформируемой среды, поведение материала не меняется (тензор напряжений поворачивается в системе отсчета наблюдателя вместе с элементарным объемом материала).
Существуют также другие объективные тензоры деформации, например, тензор деформации Альманси, тензоры деформации Пиола, Фингера и т. д. В некоторые из них входят производные от перемещений по координатам в отсчетной конфигурации (до деформирования), а в некоторые — по координатам в актуальной конфигурации (после деформирования).
То, что в классической сплошной среде энергия деформации зависит лишь от симметричного тензора деформации, следует из закона баланса моментов. Любая взаимно-однозначная функция объективного тензора деформации будет также объективным тензором деформации. Например (в силу симметричности и положительной определенности тензора деформации) можно использовать квадратный корень из тензора деформации Коши-Грина. Однако, задавая определяющие уравнения при помощи этих тензоров, важно следить за предположениями о характере зависимости свободной энергии (или напряжений) от тензоров деформации. Ясно, что предположения о, скажем, дифференцируемости свободной энергии по тензору деформации Коши-Грина, по корню из него или по его квадрату приведут к уравнениям совершенно разных материалов. Линейная по теория общего вида при малых получится лишь в первом случае.
При малых можно пренебречь квадратичными слагаемыми, и пользоваться тензором деформации в виде:
Линейный тензор деформации Коши-Грина (совпадает с линейным тензором деформации Альманси с точностью до знака) не обладает свойством материальной объективности при больших поворотах, поэтому его не используют в определяющих уравнениях для больших деформаций. В приближении малых поворотов это свойство сохраняется.
Диагональные элементы описывают линейные деформации растяжения либо сжатия, недиагональные — деформацию сдвига.
Уравнение Гельмгольца
Г.у – Гельмгольца уравнение
ГЕЛЬМГОЛЬЦА УРАВНЕНИЕ - уравнение с частными производными вида
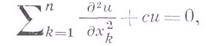
где с - постоянное число. к Гельмгольца уравнение приводит изучение установившихся колебательных процессов. При с=0 Гельмгольца. уравнение. переходит в Лапласа уравнение. В случае, если в правой части Гельмгольца. уравнение. стоит функция f(x), это уравнение называется. неоднородным.
Для Г. у., являющегося уравнением эллиптич. типа, в ограниченной области ставятся обычные краевые задачи (Дирихле, Неймана и др.). Те значения с, для к-рых существует не равное тождественно нулю решение однородного Г. у., удовлетворяющее соответствующему однородному краевому условию, наз. собственным значением оператора Лапласа (соответствующей краевой задачи). В частности, для задачи Дирихле все собственные значения положительны, а для задачи Неймана - неотрицательны. Для значений с, совпадающих с собственными значениями, решение краевой задачи для Г. у. заведомо не едннственно. Если же значения отличны от собственных, то теорема единственности справедлива.
При решении краевых задач для Г. у. применяются обычные методы теории эллиптич. уравнений (сведение к интегральному уравнению, вариационный метод, метод конечных разностей).
В случае неограниченной области с компактной границей для Г. у. ставятся внешние краевые задачи, которые при C<) имеют единственное решение, стремящееся к нулю на бесконечности. При С>0 стремящееся к нулю на бесконечности решение Г. у., вообще говоря, не является единственным. В этом случае для выделения единственного решения ставят дополнительные условия (см. Внешняя и внутренняя краевые задачи, Предельного поглощения принцип).
Для регулярного в области G решения Г. у. справедлива следующая формула среднего значения
Где 
- сфера радиуса г с центром в точке х а, целиком лежащая в области 
- Бесселя функция порядка 