12.1. Метод R-функций Рвачёва. Идея метода. Впервые понятие R-функции было введено в связи с возникшей необходимостью составлять уравнения сложных чертежей (в процессе поиска приближенных решений некоторых пространственных контактных задач теории упругости).
Со временем понятие R-функции было обобщено и возникло общее понятие R-отображения. В основе этого понятия лежит выделение из систем алгебраических операций (т.е. отображений) таких, которые в некотором смысле соответствуют функциям -значной логики. В общем виде теория R-отображений еще мало разработана. В основном изучались R-функции, которые соответствуют функциям двузначной (булевым функциям) и трехзначной логики.
В первых работах по теории R-функций был определен достаточно широкий круг возможных ее приложений: оптимальное размещение геометрических объектов (в частности, оптимальный раскрой, распознавание образов, математическое программирование (линейное и нелинейное), конструктивная теория функций и в особенности краевые задачи математической физики.
В последние годы возросли темпы создания новых математических теорий и разработки на их основе компьютерных методов решения задач исследования, расчета и оптимизации физико-механических полей, в том числе МДТТ, математическими моделями которых являются задачи для уравнений с частными производными при определенных краевых и начальных условиях.
Наличие в постановке краевых задач двух разнородных видов информации‒ аналитической и геометрической‒серьезное препятствие при создании методов и алгоритмов решения этих задач. В таких классических методах, как, например, разделения примененных и интегральных преобразований, форма областей и участков их границ учитывается благодаря подходящему выбору систем координат: в вариационных методах‒при построении координатных функций, в сеточных методах‒при составлении уравнений для узлов, близких к границе и т.д. Метод конечных элементов (МКЭ) возник именно в связи со стремлением как можно точнее учитывать геометрические формы. Появился также ряд методов (Рейснера, штрафов и др.), в которых краевые условия естественны и формально им можно не удовлетворять. В этих методах геометрическая информация учитывается путем интегрирования по областям соответствующей формы (т.е. геометрическая информация учитывается интегрально).
Особенно актуальна разработка таких методов решения краевых задач, которые имели бы универсальных характер и не требовали от исследователя знания тонких вопросов теории. Из упомянутых выше методов универсальны разностные, вариационные и конечных элементов. Можно назвать также методы Трефтца, локальных вариаций, штрафов и др. Перечисленные методы принято называть прямыми; для них характерно сведение краевых задач к решению алгебраических систем линейных уравнений. Есть, однако, более глубокая связь между этими методами, которая делает различие между ними весьма условным: во всех прямых методах приближенное решение краевой задачи отыскивается в виде
где 
‒ некоторые заранее выбранные функции, а 
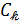‒ числа, которые находятся в результате решения упоминавшихся выше систем алгебраических уравнений. В некоторых методах (сеточных, МКЭ) формула (1) представления решения не всегда явно выписывается, однако это не меняет сути. В простейших конечно-разностных методах, например, за основу берется функция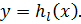 
Приближенное решение (например, для двумерной задачи) выбирается в виде линейной комбинации произведений сдвигов-сжатий функций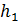 
:
Здесь 
‒ значение искомой функции в узле (𝑖, 𝑗), а 𝛼, 𝛽, 𝛾 и 𝛿 выбираются такими, чтобы функция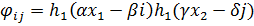 
была равна единице в (𝑖, 𝑗)-м узле и нулю в остальных узлах сетки. Нетрудно представить, что графически функция (2) ‒ это многогранная поверхность. При этом изменение какой-либо из величин 
приводит лишь к локальному ее изменению в окрестности узла (𝑖, 𝑗). Если, учтя граничные условия, подставить формулу (2) в функционал, соответствующий краевой задаче, и написать условия его экстремума, то относительно величин получим систему конечно-разностных уравнений. Другие конечно-разностные схемы получаем аналогично, используя иные функции. В этом смысле ничем по существу не отличается от сеточных методов и метод конечных элементов, в котором функции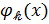 
также локальные.
В классических вариационных методах функции 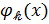‒ это так называемые координатные функции, удовлетворяющие, если это необходимо, краевым условиям. Применение таких функций приводит к системе алгебраических уравнений, как правило, с полностью заполненными матрицами. Такие системы обычно плохо обусловлены даже при сравнительно небольших 𝑁 (порядка 
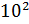), и требуют для хранения элементов матрицы в памяти компьютера 
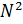ячеек. Кроме того, вычисление коэффициентов в методах типа Ритца, Бубнова-Галёркина, или наименьших квадратов, требует вычисления кратных интегралов по всей области, в которой решается задача, и как следствие‒больших затрат машинного времени. Таким образом, если взять за основу один и тот же вариационный принцип (например, минимизировать функционал Ритца), то метод сеток, конечных элементов и классический вариационный будут отличаться лишь выбором функций 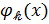. Будут различными при одном и том же 𝑁 вычислительные затраты и накопление погрешностей, что, конечно, очень важно, однако тип сходимости, вообще, будет один и тот же.
Возможен и другой вариант: функции 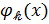выбираются одни и те же, но по-разному определяются постоянные 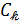. Например, используя одну и ту же формулу (1), можно находить постоянные по методу Ритца, а можно, добавив к функционалу Ритца соответствующие слагаемые, применить метод Куранта и получить, благодаря этому, более высокий тип сходимости, чем сходимость по энергии.
Таким образом, все прямые методы объединяет между собой формула (1), а отличие между ними состоит лишь в выборе функций 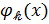и способа отыскания постоянных .
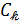В большинстве случаев требуется, а в остальных желательно, чтобы функции 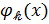удовлетворяли краевым условиям рассматриваемой задачи. Основная трудность в решении этого вопроса связана с тем, что в формулы, представляющие функции 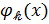, должна некоторым образом включаться информация геометрического характера о форме границы рассматриваемой области (и форме ее участков для краевых условий смешанного типа). В некоторых методах (сеточных, МКЭ) эта информация учитывается приближенно вследствие локального приближения узлов сетки к границе, а в некоторых (Рейсснера, штрафов) ‒ в интегральном смысле. Это, конечно, накладывает определенных отпечаток на тип сходимости и величину погрешностей. Тем не нее с этими недостатками можно было бы смириться при условии, что погрешность в результате приближенного учета геометрических форм соразмерна с погрешностью самого приближенного метода. Однако есть еще один весьма важный фактор, который необходимо учитывать: и в сеточных методах, и в МКЭ составление уравнений для пограничных узлов трудно формализуемое, что затрудняет решение вопросов автоматизации программирования. Эта проблема может быть решена с помощью конструктивного аппарата теории R-функций. При этом речь идет о краевых условиях самых различных типов для областей практически произвольной формы. Для линейных краевых условий получаются формулы вида (1), а для нелинейных ‒ формулы общего вида:
С точки зрения теории приближений одного лишь удовлетворения краевым условиям недостаточно для того, чтобы можно было получать приближения к точному решению. Задачу можно считать успешно решенной лишь при обеспечении определенных аппроксимационных свойств функций 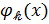: их линейные комбинации (1) должны достаточно хорошо приближать функции того класса, которому принадлежит точное решение задачи, т.е. функции (1) должны удовлетворять условиям полноты, а по возможности и условию аппроксимационной универсальности.
Основное внимание обращено на конструктивную сторону теории R-функций, позволивших во много раз сократить затраты на составление и отладку программ при решении краевых задач.