Выводы
1. В настоящее время для оценки средних годовых концентраций загрязняющих веществ (ЗВ) в речном стоке в основном используются два метода. В первом из них учитывается водность реки в период отбора проб на химанализ и расчётная величина средней годовой концентрации определяется как среднее взвешенное по расходу воды значение. Во втором методе расчётная величина средней годовой концентрации определяется без учёта водности, как среднее арифметическое значение по всем измеренным значениям концентраций.
2. Теоретической основой второго метода является предположение о постоянстве расходов воды в течение года, что не соответствует действительности. Однако из-за отсутствия по многим пунктам наблюдений за расходами воды именно второй метод расчета средних годовых концентраций получил наибольшее распространение. В связи с этим встает вопрос о погрешностях расчетов средних годовых концентраций к которым может привести необоснованное использование второго метода
3. Результаты исследования показали, что возможные погрешности расчета средних годовых концентраций за счёт не учёта водности достигают очень больших значений. Так, для р. Охты погрешность расчета средних годовых концентрации варьирует от -40 % до 170 %. Для р. Великой, за счёт более детального учёта внутригодовых колебаний водности реки, погрешности варьируют – от -60 % до 500 %.
4. Неучёт водности при оценках средних годовых концентраций в существенной степени сказывается и на числовых характеристиках средних многолетних средних годовых концентраций ТМ. Так по всем ТМ, за исключением железа, средние многолетние значения средних годовых концентраций увеличиваются по отношению к средним многолетним средним годовым концентрациям, рассчитанным с учётом водности, на величину от 2 до 120%.
5. Таким образом, неучёт водности в период отбора проб может привести к значительным погрешностям расчётов средних годовых и средних многолетних концентраций, большей частью в сторону преувеличения, что в свою очередь приведет к аналогичному преувеличению объемов стока загрязняющих веществ через заданный створ. Поэтому во всех случаях необходимо использовать первый метод оценки средних годовых концентраций, учитывающий водность в период взятия проб на химаналих.
6. При отсутствии наблюдений за расходами воды можно воспользоваться районным типовым суточным гидрографом, что позволит, при надлежащем анализе, сократить возможные погрешности определения средних годовых концентраций в 1,5 – 2 раза.
Литература
1. Никаноров А.М., Гидрохимия. - Ленингад.: Гидрометеоиздат, 1989.- 352 с. 
2. Фадеев В.В., Тарасов М.Н., Павелко В.Л. Зависимость минерализации и ионного состава воды рек от их водного режима. – Л.: Гидрометеоиздат, 1989, 176 с.
3. Орлов В.Г., Скакальский Б.Г., Бесценная М.А., Шварцман А.Я., Меерович Л.Н. Контроль качества поверхностных вод. Учебное пособие. Л., изд. ЛПИ, 1988, 140 с. (ЛГМИ)
4. Шелутко В.А. Численные методы в гидрологии. Л. Гидрометеоиздат, 1991, 130 с.
2 Неэквидистентность исходной информации и методика её учёта при оценке среднегодовой конценрации и объемов стока биогенных веществ
Как было отмечено раннее, принятые в настоящее время методы оценки среднегодовой концентрации основываются на следующих базовых теоретических положениях:
1) временные ряды измеренных значений концентраций содержащихся в воде веществ в каждом пункте наблюдений описываются моделью в виде ряда значений случайной величины;
2) данные ряды наблюдений являются стационарными, регулярными и однородными.
Однако, как было показано ранее в главе 2, далеко не всегда имеющиеся ряды измеренных значений концентраций растворённых в воде веществ (ряды наблюдения) удовлетворяют указанным положениям. В частности, исходные ряды наблюдений не являются регулярными, то есть временные промежутки между наблюдениями не являются равными. Такие временные ряды в математике называются неэквидистентными (Афифи, 1982).
Причина нерегулярности наблюдений кроется в самих требованиях РД 52.24.309-2004 к периодичности отбора проб. Как уже указывалось ранее, в соответствии с руководящим документом пробы необходимо отбирать в основные фазы водного режима, продолжительность и время наступления которых в силу естественных причин меняется год от года (РД 52.24.309-94, РД 52.24.309-2004, ГОСТ 17.1.3.07-82). Таким образом, априори все ряды наблюдений за гидрохимическими показателями являются неэквидистентными, т.е. измерения не являются равноудалёнными во времени. Другой причиной нерегулярности наблюдений, может быть не менее важной, является пропуск в наблюдениях и изменений сроков наблюдений по той или иной причине.
Между тем, принятые в настоящее время методики оценки среднегодовой концентрации не учитывают внутригодовой нерегулярности наблюдений. В связи с этим возникла необходимость разработки методики учёта неэквидистентности исходной гидрохимической информации.
4.1 Разработка методики расчета среднегодовой концентрации с учетом неэквидистентности исходных рядов
Как уже отмечалось в настоящее время при обработке гидрохимических наблюдений, независимо от количества проб в году, за среднегодовую концентрацию принимается среднеарифметическое или средневзвешенные по расходам воды значение измеренных за год концентраций (2.22, 2.23). Поскольку ряды гидрохимических данных являются неэквидистентными (НЭ), возникает вопрос о точности таких расчетов и объективности выводов, полученных на их основе. Для ответа на этот вопрос необходимо разработать метод, который при расчетах средних значений позволил бы учитывать неодинаковые интервалы между наблюдениями.
На рисунке 4.1 и рисунке 4.2 в качестве примера представлены календарные графики измеренных значений концентраций растворенного в воде вещества в течение года при 4 и 7 измерениях в год. Здесь же представлены концентрации по последнему измерению за предшествующий год и первому измерению за последующий год.
Для точного определения средней величины концентрации за год (в предположении о линейном характере изменений концентраций между точками измерений) необходимо определить площадь заштрихованной фигуры и разделить ее на число дней в году.
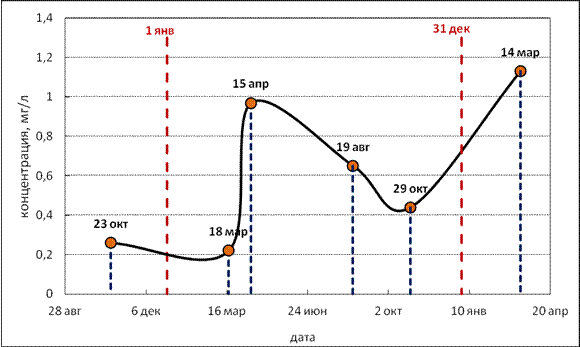
Рисунок 4.1 − График измеренных значений концентраций аммонийного азота за 1977 г., р. Великая – г. Псков, верхний створ
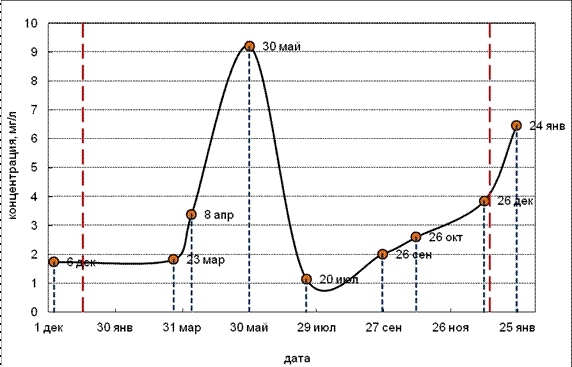
Рисунок 4.2 − График измеренных значений БПК5 за 1973 г., р. Великая - г. Псков, верхний створ
Для определения площади обычно используется метод трапеций, то есть площадь всей заштрихованной фигуры определяется как сумма площадей трапеций, опирающихся одной боковой стороной на ось абсцисс. В качестве основания трапеций служат линии параллельные оси ординат и проходящие от оси абсцисс к измеренному значению концентрации.
Площадь трапеций определяется как полусумма оснований (среднее значение между соседними измеренными концентрациями) умноженная на высоту трапеции (число дней между измерениями концентраций), то есть:
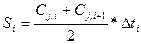(4.1)
где Cj,i, Cj,i+1 – измеренные значения концентраций растворенного в воде вещества,
j – год измерений,
i – порядковый номер измерения в J-ом году, i = 1, 2, …, k-1,
k – число измерений концентраций в год,
Δti – число дней между i –ым и i+1 -ым измерением концентрации.
Отсюда площадь заштрихованной фигуры между первым и последним измерением концентраций в данном году вычисляется по формуле:
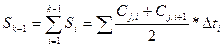(4.2)
Трапеции, расположенные в начале и конце года, как правило, являются незамкнутыми и границы их переходят на предыдущий или последующий год. Для расчета площадей этих трапеций в пределах данного j -го года необходимо знать концентрации растворенного вещества в начале – 1января (Снг ,) и в конце – 31 декабря (Скг) данного года. Эти значения определяются линейной интерполяцией соответственно между первым измеренным значением концентрации в данном году и последним значением в предшествующем году и между последним измеренным значением концентрации в данном году и первым измеренным значением концентрации в последующем году:
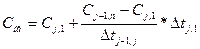(4.3)
где Сj,1 – 1-е измеренное значение концентрации в рассматриваемом j -м году;
Сj-1,n – последние значение концентрации в предыдущем j-1 -м году;
Δtj-1,j – временной интервал (число дней) между датой последнего значения концентрации в предыдущем году и датой первого значения концентрации в рассматриваемом году;
∆tj,1 – временной интервал между началом года и датой первого измерения концентрации в рассматриваемом году, дней.
Аналогично концентрация на 31 декабря j -го года Cкг определяется по формуле
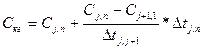(4.4)
где Cj,n – последнее n -е значение концентрации в рассматриваемом j -м году;
n – число измерений концентраций в рассматриваемом году;
Cj+1,1 – 1-е значение концентрации в последующем j+1 -м году;
Δtj,j+1 – временной интервал в днях между датами последнего значения концентрации в рассматриваемом году и 1-го значения концентрации в последующем году;
∆tj,n – временной интервал между концом года и датой последнего (n -го) измерения концентрации в рассматриваемом году, дней.
Обозначим через Sнг часть площади трапеции в начале j -го года, приходящуюся на этот год; а часть площади трапеции в конце года, приходящуюся на этот год, через Sкг. Для расчета их этих площадей можно воспользоваться формулами (4.5) и (4.6):
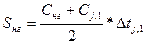, (4.5)
где Снг – значение концентрации в начале рассматриваемого года;
Сj,1 – 1-е значение концентрации в рассматриваемом j -м году;
∆tj,1 – временной интервал между началом года и датой первого измерения концентрации в рассматриваемом году, дней.
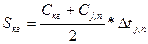. (4.6)
где Скг – значение концентрации в конце рассматриваемого года;
Cj,n – n -е значение концентрации в рассматриваемом j -м году;
∆tj,n – временной интервал между концом года и датой n-го измерения концентрации в рассматриваемом году, дней.
По формулам (4.2), (4.5) и (4.6) можно определить площадь концентраций на рисунках 4.1 и 4.2:
S=Sk-1 + Sнг + Sкг ,(4.7)
и, разделив S на число дней в году, получить среднее годовое значение концентрации то есть:
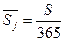. (4.8)
Приняв в формулах (4.1-4.6) значения Δt постоянными можно получить формулу расчета средней годовой концентрации, принятую в настоящее время (формула 2.23) (Смыжова, Шелутко, 2008).
4.2 Оценка среднегодовых концентраций с учетом неэквидистентности исходных рядов
На основе полученных формул можно сопоставить результаты расчетов с учетом и неучетом неэквидистентности и выявить эффективность или неэффективность учета неэквидистентности при оценке средней годовой концентрации химических веществ и показателей. Для этого, как и в предыдущем случае при оценке эффективности учета водности необходимо сопоставить результаты расчетов средней годовой концентрации обычно принятым методом (формула (2.23) и методом с учетом неэквидистентности (формула (4.8). С этой целью по каждому из 8 показателей отдельно для каждого года, на каждом пункте были рассчитаны среднегодовые значенияе концентраций тем и другим способом. По полученным рядам среднегодовых концентраций были рассчитаны средние многолетние значения S ср по формуле (2.1), средние квадратические отклонения (СКО) по формуле (2.2), коэффициенты вариации (Cv) по формуле (2.3) и коэффициенты асимметрии (Cs) по формуле (2.4) ряда среднегодовых концентраций рассчитанных обоими способами. Погрешности и относительные погрешности расчетов среднегодовых концентраций за счет неучета неэквидистентности определялись по формулам:
∆i=Sai-Sнэi, (4.9)
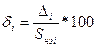. (4.10)
где Sai – среднегодовая концентрация, рассчитанная как среднеарифметическое значение; Sнэi – среднегодовая концентрация, рассчитанная с учётом неэквидистентности
Как следует из данных, представленных в таблицах приложения Е, неучет неэквидистентности приводит к довольно большим ошибкам определения среднегодовых концентраций. Например, в 1991 году значения концентрации нитратного азота в пункте Опочка (н. створ) составили при расчетах без учета и с учетом неэквидистантности рядов соответственно 0,260 и 0,147 мг/дм3 (таблица Е.4). В этом же году значения средней годовой концентрации минерального фосфора в пункте Остров (в. створ) составили при расчетах без учета и с учетом неэквидистантности рядов соответственно 0,003 мг/дм3 и 0,018 мг/дм3. (таблица Е.6). Таким образом, учет неэквидистентности может привести как к увеличению, так и снижению средней годовой концентрации. При этом, снижение или увеличение среднегодовых концентраций за счет учета неэквидистентности определяется двумя причинами: 1) внутригодовым распределением дат взятия проб на химанализ; 2) соотношением значений концентраций по последнему измерению в предшествующем году и первому измерению в последующем году, и / или по последнему измерению в данном году и первому в последующем году использование при оценке среднегодовой концентрации с учётом НЭ последнего измерения в предшествующем году и первого измерения в последующем году, т.к. иногда эти значения могут быть больше или меньше измеренных значений концентрации в исследуемом году.
По рядам значений относительной погрешности оценки среднегодовых концентраций за счет неучета водности (δ,%) был произведён расчёт среднего значения, СКО и Cs (приложение Е).
Как следует из представленных в приложении Е и в таблице 4.1 данных, возможные ошибки определения среднегодовых концентраций за счет неучета неэквидистентности исходных рядов составляет от 0 до 200 % и более. Например, в г. Опочка (нижний створ) максимальная погрешность определения концентрации нитритного азота в 1971 году составила 239 % (таблица Е.4), также большая погрешность (209 %) получилась для NO2 в пункте Псков на верхнем створе в 1973 году. В пункте Остров (в. створ) для минерального фосфора максимальная погрешность 94% получилась в 1979 году (таблица Е.6).
Таблица 4.1 – Экстремальные значения относительной погрешности δ, %
| вещество | пункт наблюдения | ||||||
| Опочка в.с. | Опочка н.с. | Остров в.с. | Остров н.с. | Псков в.с. | Псков н.с. | ||
| аммонийный азот | макс | ||||||
| мин | -69 | -100 | -44 | -53 | -67 | -15 | |
| нитратный азот | макс | ||||||
| мин | -48 | -24 | -35 | -20 | -46 | -33 | |
| нитритный азот | макс | ||||||
| мин | -100 | -100 | -100 | -74 | -55 | -47 | |
| минеральный фосфор | макс | ||||||
| мин | -85 | -59 | -84 | -51 | -46 | -41 | |
| общее железо | макс | ||||||
| мин | -100 | -30 | -76 | -84 | -77 | -70 | |
| растворённый кислород | макс | ||||||
| мин | -5 | -7 | -5 | -3 | -3 | -2 | |
| БПК5 | макс | ||||||
| мин | -36 | -49 | -12 | -10 | -16 | -5 | |
| ХПК | макс | ||||||
| мин | -16 | -13 | -14 | -40 | -19 | -14 |
Следует отметить (табл. 4.1), что наибольшие значения погрешностей расчета среднегодовых концентраций за счет неучета неэквидистентности исходных данных получились для концентраций нитритного азота, общего железа и минерального фосфора. Возможно, это объясняется высокой степенью внутригодовой изменчивости концентраций этих элементов и тем, что исходные ряды наблюдений за этими элементами имеют наименьшую длину, по сравнению со всеми остальными рядами.
Наименьшую погрешность расчетов за счёт неучёта неэквидистентности имеют концентрации кислорода. Возможно, это объясняется большей устойчивостью кислородного режима и малой внутригодовой изменчивостью его концентраций.
Для более наглядного представления о разбросе экстремальных значений погрешности за счёт неучёта неэквидистентности был построен график, представленный на рисунке 4.3.
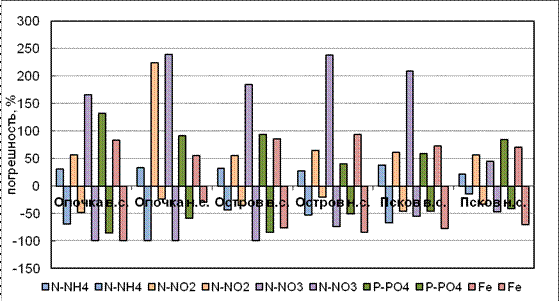
Рисунок 4.3 – Экстремальные погрешности оценки среднегодовой концентрации различных форм азота, минерального фосфора и общего железа при неучёте неэквидистентности
Здесь интересно отметить, что почти по всем элементам, кроме нитритного азота, погрешности определения среднегодовых концентраций в положительную и отрицательную сторону примерно одинаковы. Как следует из графика, величины экстремальных значений погрешностей в основном имеют примерно одинаковые значения, как в положительной, так и в отрицательной части графика. При этом наибольшие значения погрешностей, превышающие 100%, характерны в основном только для концентраций нитритного азота, и лишь в пункте Опочка (н. створ) для нитратного азота погрешность превышает 200 %.
В некоторых случаях среднегодовые значения с учетом и без учета неэквидистентности естественно отличались незначительно. Так, например, в 1972 году в пункте Псков (в. створ) среднегодовое содержание кислорода в р. Великой равно 10,5 мг/дм3 при расчете принятым методом, а при расчете с учетом неэквидистентности ряда среднегодовое содержание кислорода за этот же год составило 10,3 мг/дм3 (таблица Е.9). Ещё одним примером могут служить значения среднегодовой концентрации общего железа в 1998 году в пункте Опочка (в. створ): 0,020 мг/дм3 и 0,021 мг/дм3 при расчёте без учёта и с учётом неэквидистентности (таблица Е.1).
Для более детального анализа погрешностей расчёта среднегодовых концентраций, за счёт неучёта водности, были построены эмпирические кривые обеспеченности значений погрешностей.
При этом, как уже отмечалось в 3 разделе, так как по каждому отдельному ряду наблюдений полученной информации было недостаточно для обоснованных выводов, относительные погрешности δ (%), полученные для одного вещества на всех исследуемых створах были объединены в одну последовательность. В результате объединения были получены ряды с числом членов от 122 до 202. Полученные объединенные ряды ранжировались в убывающем порядке, и для каждого члена ряда рассчитывалась эмпирическая обеспеченность по формуле (2.11)
Затем ранжированные последовательности наносились в поле клетчатки вероятности с умеренной асимметричностью. На рисунке 4.4 в качестве примера представлены наиболее интересные эмпирические кривые обеспеченности относительных погрешностей расчетов среднегодовых концентраций в процентах за счет неучета водности для минерального фосфора (а), нитритного азота (б) и ХПК (в).
Обращает на себя внимание отличие вида построенных эмпирических кривых обеспеченностей погрешностей от обычно принятого в гидрологии. Здесь и в левой (Р ≤ 5%) и в правой части (Р ≥ 90 -95 %) графика эмпирические точк и резко отклоняются от общей тенденции. Попытка объяснить это обстоятельство пока не привела к успеху.
На эмпирической кривой обеспеченности погрешностей расчёта среднегодовых концентраций минерального фосфора достаточно хорошо описывается нормальным законом распределения (рисунок 4.4 (а)). При этом положительные и отрицательные погрешности меняются по абсолютной величине в пределах от 0 до 100 %, и вероятность отрицательных и положительных погрешностей примерно одинакова. Таким образом, неучет неэквидистентности при расчетах среднегодовых концентраций приводит в 50 % случаев, как к завышению, так и к занижению их значений по сравнению с действительными значениями концентраций минерального фосфора в воде. В 10 % случаев завышение и занижение достигает от 30 до 100 и более процентов.
Закон распределения относительных погрешностей расчета среднегодовых концентраций нитритного азота имеет явно выраженную положительную асимметрию. При этом положительные погрешности по абсолютной величине намного больше, чем отрицательные. Так, положительные погрешности меняются в пределах от 0 до 240 %, а отрицательные в пределах от 0 до минус 100 %, Вместе с тем вероятность положительных и отрицательных погрешностей примерно одинакова и равна 50 %. В 40 % случаев погрешность равна или близка к нулю. Таким образом, неучет водности при расчетах среднегодовых концентраций нитритного азота приводит в 60 % случаев к завышению или к занижению их значений по сравнению с действительными значениями.
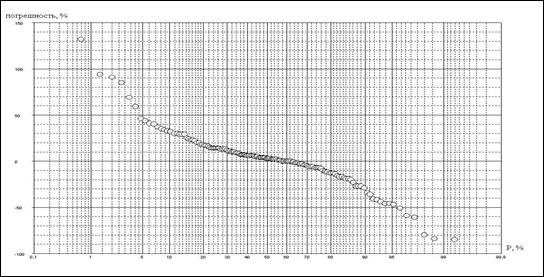
(а) – минеральный фосфор
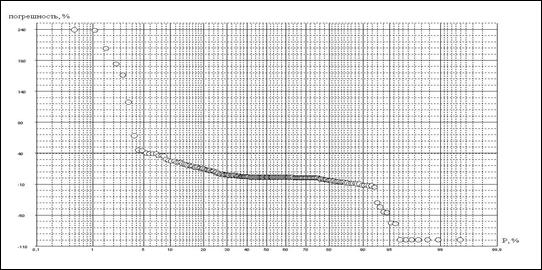
(б) – нитритный азот
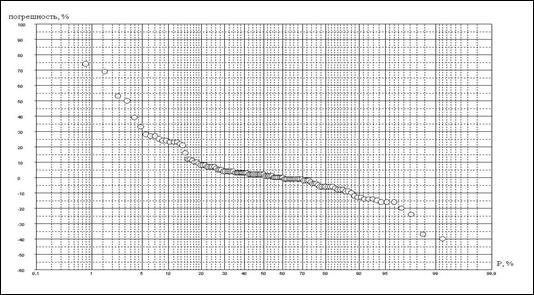
(в) - ХПК
Рисунок 4.4 – Эмпирические кривые обеспеченности значений погрешности δ,% за счёт неучёта неэквидистентности
Закон распределения относительных погрешностей расчета среднегодовых концентраций ХПК за счет неучета неэквидистентности имеет в верхней части явно выраженную положительную асимметрию. При этом положительные погрешности по абсолютной величине несколько больше, чем отрицательные. Так, положительные погрешности меняются в пределах от 0 до примерно 75 %, а отрицательные в пределах от 0 до минус 40 %, Вероятность положительных погрешностей составляет 60 %, а отрицательных – 40 %. Таким образом, неучет неэквидистентности исходных данных приводит чаще всего к завышению среднегодовых концентраций ХПК при расчетах среднегодовых концентраций. В 10 % случаев завышение достигает от 20 до 70 и более процентов, а занижение от 15 до 100 и более %.
Законы распределения погрешностей расчета среднегодовых концентраций при неучете неэквидистентности других элементов, рассматриваемых в диссертации, имеют такие же особенности, как и законы распределения минерального фосфора и нитритного азота.
В таблице 4.5 представлены средние многолетние значения рядов среднегодовых концентраций рассчитанных без учета и с учетом неэквидистентности.
Как следует из представленных данных, в большинстве случаев значение средней многолетней концентрации, рассчитанной без учета неэквидистентности, по среднеарифметическим значениям среднегодовых концентраций, немного больше, чем многолетние значения, рассчитанные по рядам среднегодовых концентраций, найденных с учетом неэквидистентности рядов.
В двух случаях из 48 (нитритный азот, г. Псков, н. створ; ХПК, г. Остров, н. створ) при учете неэквидистентности наблюдается некоторое увеличение средней многолетней концентрации. Однако, лишь в одном случае (г. Остров) оно является статистически значимым.
Таблица 4.5 – Значения средних многолетних концентраций (мг/дм3) по основным гидрохимическим показателям с учетом и неучетом неэквидистнтности р. Великая
| Вещество | Верхний створ | Нижний створ | ||
| Sa | Sнэ | Sa | Sнэ | |
| г. Псков | ||||
| Растворённый кислород | 9,9 | 9,7 | 9,7 | 9,3 |
| ХПК | 32,1 | 31,1 | 31,3 | 30,4 |
| БПК5 | 1,94 | 1,87 | 2,2 | 2,1 |
| Аммонийный азот | 0,229 | 0,214 | 0,226 | 0,223 |
| Нитритный азот | 0,009 | 0,008 | 0,016 | 0,017 |
| Нитратный азот | 0,430 | 0,417 | 0,50 | 0,48 |
| Минеральный фосфор | 0,017 | 0,015 | 0,018 | 0,017 |
| Общее железо | 0,134 | 0,131 | 0,149 | 0,140 |
| г. Остров | ||||
| Растворённый кислород | 10,1 | 9,8 | 10,0 | 9,8 |
| ХПК | 28,6 | 28,2 | 26,4 | 26,9 |
| БПК5 | 1,6 | 1,5 | 2,0 | 1,9 |
| Аммонийный азот | 0,179 | 0,170 | 0,19 | 0,18 |
| Нитритный азот | 0,0050 | 0,0045 | 0,008 | 0,007 |
| Нитратный азот | 0,338 | 0,313 | 0,371 | 0,349 |
| Минеральный фосфор | 0,012 | 0,012 | 0,015 | 0,014 |
| Общее железо | 0,125 | 0,116 | 0,108 | 0,101 |
| г. Опочка | ||||
| Растворённый кислород | 10,4 | 10,1 | 9,9 | 9,6 |
| ХПК | 21,3 | 20,4 | 21,3 | 20,4 |
| БПК5 | 1,81 | 1,76 | 2,29 | 2,22 |
| Аммонийный азот | 0,0998 | 0,0995 | 0,116 | 0,111 |
| Нитритный азот | 0,0039 | 0,0038 | 0,0132 | 0,0129 |
| Нитратный азот | 0,300 | 0,287 | 0,365 | 0,354 |
| Минеральный фосфор | 0,019 | 0,019 | 0,021 | 0,020 |
| Общее железо | 0,055 | 0,049 | 0,061 | 0,056 |
Таким образом, можно сделать вывод, что, несмотря на существенные различия отдельных значений среднегодовых концентраций за счёт неучёта неэквидистентности, средние многолетние значения концентраций различаются менее значительно или не различаются совсем.
В таблице 4.6 представлены результаты расчетов коэффициентов вариации (Cv) рядов среднегодовых концентраций, рассчитанных с учётом и без учёта неэквидистентности.
Таблица 4.6 – Значения коэффициентов вариации рядов среднегодовых значений концентраций, рассчитанных без учета и с учетом неэквидистентности. р. Великая
| Вещество | Верхний створ | Нижний створ | ||
| Cva | Cvнэ | Cva | Cvнэ | |
| г. Псков | ||||
| Растворённый кислород | 0,07 | 0,07 | 0,079 | 0,091 |
| ХПК | 0,29 | 0,29 | 0,20 | 0,24 |
| БПК5 | 0,20 | 0,24 | 0,37 | 0,38 |
| Аммонийный азот | 1,12 | 1,12 | 1,22 | 1,24 |
| Нитритный азот | 0,90 | 0,82 | 1,32 | 1,34 |
| Нитратный азот | 0,58 | 0,58 | 0,71 | 0,68 |
| Минеральный фосфор | 0,98 | 0,88 | 0,56 | 0,54 |
| Общее железо | 0,75 | 0,67 | 0,749 | 0,667 |
| г. Остров | ||||
| Растворённый. кислород | 0,087 | 0,094 | 0,094 | 0,092 |
| ХПК | 0,21 | 0,21 | 0,28 | 0,25 |
| БПК5 | 0,28 | 0,27 | 0,30 | 0,29 |
| Аммонийный азот | 1,16 | 1,18 | 1,24 | 1,24 |
| Нитритный азот | 0,76 | 0,61 | 1,12 | 0,99 |
| Нитратный азот | 0,46 | 0,43 | 0,46 | 0,47 |
| Минеральный фосфор | 0,90 | 0,74 | 0,81 | 0,67 |
| Общее железо | 0,66 | 0,68 | 0,69 | 0,66 |
| г. Опочка | ||||
| Растворённый кислород | 0,094 | 0,096 | 0,11 | 0,10 |
| ХПК | 0,42 | 0,37 | 0,46 | 0,39 |
| БПК5 | 0,37 | 0,38 | 0,50 | 0,47 |
| Аммонийный азот | 1,12 | 1,09 | 1,07 | 1,04 |
| Нитритный азот | 1,12 | 1,13 | 1,33 | 1,30 |
| Нитратный азот | 0,618 | 0,551 | 0,65 | 0,61 |
| Минеральный фосфор | 2,05 | 1,94 | 0,83 | 0,75 |
| Общее железо | 0,87 | 0,82 | 0,92 | 0,92 |
Как следует из этих данных Cv ряда средневзвешенных по времени концентраций в большинстве случаев меньше, чем Cv ряда средних концентраций рассчитанных традиционным способом (35 случаев из 48). Исключениями являются значения Cv растворённого кислорода в пункте Псков − н. створ, Остров − в. створ и Опочка – н. створ; ХПК в пункте Псков – н. створ; БПК5 в пунктах Псков – в. и н. створы, Опочка – в. створ; аммонийного азота в пункте Псков – нижний створ и Остров (в. створ); нитритный азот в пунктах Псков – н. створ и Опочка – в. створ; нитратного азота в пункте Остров (н.створ); общее железо в пункте Остров – в. створ. Однако в большинстве случаев расхождения Cv являются статистически не значимыми.
Это говорит о том, что ряд средневзвешенных по времени значений концентраций является более сглаженным, так как при не учете продолжительности временных интервалов, на естественные колебания значений концентраций накладывается случайная составляющая, связанная с изменением продолжительности интервалов. Интересно, что за счет уменьшения Cv в значительной степени уменьшаются возможные максимальные значения концентраций биогенных элементов обеспеченностью 1 и 0,1 %.
Как уже отмечалось ранее, значения среднегодовых концентраций растворённых в воде веществ являются основой для дальнейшего анализа загрязнённости водотока. В частности именно среднегодовые значения концентраций лежат в основе оценки пространственной и временной динамики загрязнения. В связи с этим рассмотрим влияние неучёта неэквидистентности при расчёте среднегодовых концентраций биогенных элементов на результаты временной и пространственной динамики загрязнения реки Великая.
На рисунках 4.5, 4.6 и 4.7 представлена временная динамика изменения содержания нитратного азота, минерального фосфора и нитритного азота в различных пунктах наблюдения при расчёте с учётом и без учёта неэквидистентности.
Рисунок 4.5 – Хронологический график изменения среднегодовой концентрации нитратного азота в реке Великая – п. Опочка (н. створ) при оценке с учётом и без учёта неэквидистентности
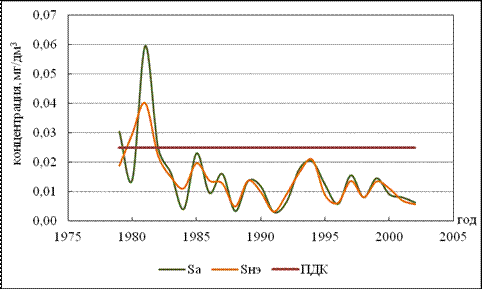
Рисунок 4.6 – Хронологический график изменения среднегодовой концентрации минерального фосфора в реке Великая – п. Остров (н. створ) при оценке с учётом и без учёта неэквидистентности
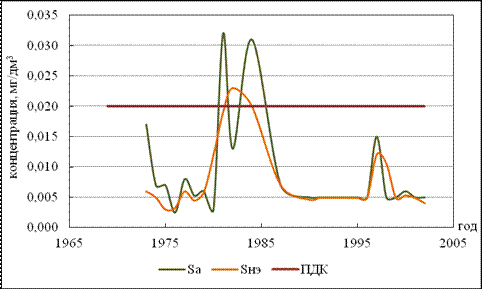
Рисунок 4.7 – Хронологический график изменения среднегодовой концентрации нитритного азота в реке Великая – п. Псков (н. створ) при оценке с учётом и без учёта неэквидистентности
Из графиков видно, что ряды значений средневзвешенных по времени концентраций имеют более сглаженные максимумы. Во многом графики среднегодовых концентраций, рассчитанных с учётом и без учёта неэквидистентности повторяют друг друга, то есть при обоих способах расчета мы можем проследить многолетнюю динамику содержания того или иного вещества в водах реки Великая, но при втором способе расчета это будет сделано точнее. Однако, несмотря на сходство общей динамики загрязнения при обоих способах расчёта, из представленных примеров можно увидеть примеры получения противоречивых выводов при расчёте с учётом и без учёта НЭ. Например, из рисунка 4.6 видно, что в период с 1979 по 1981 год при расчёте среднегодовой концентрации общепринятым способом мы отмечаем сначала спад, а затем резкий подъем значений, в то время как при расчёте с учётом НЭ мы видим плавный подъем значений. Другим ярким примером может служить ситуация показанная на рисунке 4.7. Здесь в 1981 и 1984 годах в зависимости от способа расчёта среднегодовой концентрации мы видим либо превышение значений ПДК и существенное увеличение значений концентрации (при расчёте как среднеарифметическое значений), либо среднегодовые значения концентрации нитритного азота не превышают значения ПДК в указанные годы (при учёте НЭ). Отдельного рассмотрения заслуживают примеры, когда общая тенденция загрязнения при обоих способах расчёта идентична, но конкретное значение среднегодовой концентрации превышает ПДК. Здесь, как видно из примера, представленного на рисунке 4.6, могут быть получены противоречивые выводы о кратности превышения ПДК в зависимости от способа расчёта. Так, при неучёте неэквидистентности мы видим превышение ПДК более чем в 2 раза, тогда как при учёте НЭ данное превышение существенно ниже.
Анализ пространственной динамики загрязнения в отдельные годы показал, что в большинстве случаев общая динамика распространения загрязнения прослеживается при обоих способах расчёта. Следует отметить, что в большинстве случаев значение среднегодовой концентрации, рассчитанное с учётом неэквидистентности, меньше среднегодового значения, рассчитанного как среднеарифметическое. Однако в отдельных случаях в оценке простарнственной динамики могут быть получены противоречивые выводы, зависящие от способа расчёта среднегодовой концентрации. На рисунке 4.8 представлена пространственная динамика распространения общего железа (а) и аммонийного азота (б) за 1985 год.
Так, из рисунка 4.8 (а) видно, что при расчёте среднегодовой концентрации аммонийного азота без учёта НЭ, содержание данного элемента в воде уменьшается от створа 1 к створу 2 в пунктах Опочка и Псков, тогда как при расчёте среднегодовой концентрации с учётом неэквидистентности мы видим незначительное увеличение содержания аммонийного азота на данных участках реки Великая. Следовательно, в зависимости от выбранного способа расчёта среднегодовой концентрации могут быть получены противоречивые выводы.
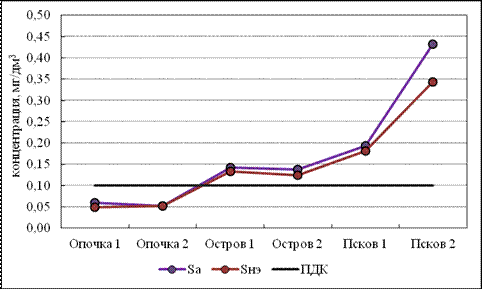
(а) – общее железо
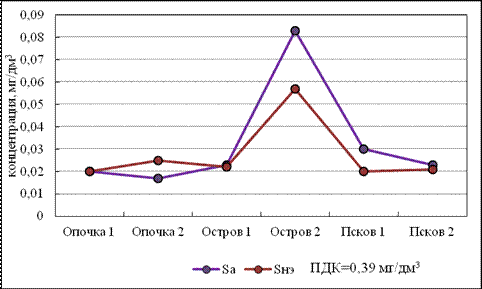
(б) ‑ аммонийный азот
Рисунок 4.8 – Пространственная динамика распространения общего железа и аммонийного азота по длине реки Великая за 1985 год
Таким образом, в результате проведенного в этом разделе исследования были получены следующие выводы: разработана методика учета неэквидистентности при расчетах среднегодовых концентраций загрязняющих веществ и проведен анализ эффективности учета неэквидистентности исходных рядов наблюдений при оценке среднегодовых концентраций загрязняющих веществ. При этом показано, что: На этой основе получены следующие выводы
1. Погрешности за счёт неучёта неэквидистентности в отдельные годы могут достигать 100 % и более.
2. Погрешности могут быть положительными и отрицательными, поэтому при достаточно продолжительных рядах наблюдений средние многолетние значения, рассчитанные с учетом и без учета неэквидистентности практически совпадают. Для коротких рядов наблюдений средние арифметические значения могут существенно отличаться от действительных, рассчитанных с учетом неэквидистентности.
3. Гораздо большие положительные отклонения получены в значениях среднеквадратических отклонений и коэффициентов вариации рядов среднегодовых концентраций. Поэтому в большинстве случаев не учёт неэквидистентности приводит к завышению возможных экстремальных значений.
4. Таким образом, во избежание крупных ошибок необходимо учитывать неэквидистентность исходных рядов наблюдений за концентрациями биогенных веществ и показателями биогенного загрязнения по разработанной методике.
3. Учет неоднородности по числу измерений
АНАЛИЗ ВЛИЯНИЯ ЧИСЛА ИЗМЕРЕНИЙ В ГОД НА ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ СРЕДНЕГОДОВЫХ КОНЦЕНТРАЦИЙ РАСТВОРЁННЫХ ВЕЩЕСТВ В РЕКАХ
Постановка задачи
К