Васильевой Д. И.
УМК «Школа России», М.И. Моро
Класс: 3 (1 ч.), стр. 82.
Тип урока: «Урок формирования умений»
Тема: «Решение задач на нахождение четвертого пропорционального первого вида»
Цель: Совершенствовать умение решать задачи на нахождение четвертого пропорционального первого вида
Задачи:
1. Актуализировать знания, умения и навыки, необходимые для решения задачи.
2. Формировать умения читать и понимать задачу; выделять структурные компоненты задачи.
3. Формировать умения составлять план решения задачи;рассуждать от данных к вопросу и наоборот; строить умозаключение; устанавливать связи между данными и искомым и выбирать арифметические действия, соответствующие этим связям, расставлять их по порядку.
4. Формировать умения записывать решение; составлять пояснения; находить значение выражений и составлять ответ.
5. Совершенствовать умения выполнять проверку способом составления обратной задачи.
Оборудование: презентация
Ход урока:
| Этапы урока | Содержание деятельности учителя и ученика | Оформление доски и презентация | |||||||||||||||||
| 1.Подготовительная работа к решению задачи. | - Обратите внимание на доску.
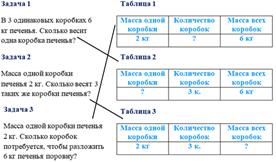
- Какую тройку величин вы видите в таблице? (масса 1 предмета / количество предметов / общая масса) - Что обозначает каждая величина? Масса 1 предмета - это число, которое показывает какова масса 1 предмета, о котором говорят в задаче. Количество предметов - это число, которое показывает сколько предметов, о которых говорят в задаче. Общая масса - это число, которое показывает какова масса всех предметов, о которых говорят в задаче. - Перед вами задачи и таблицы. Давайте соотнесём задачу с её краткой записью.
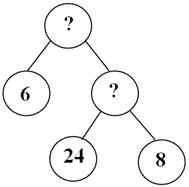
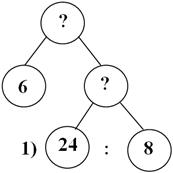
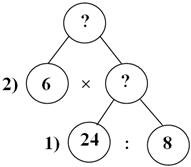
Рассмотрим первую задачу. В 3 одинаковых коробках 6 кг печенья. Сколько весит одна коробка печенья? - Устно заполним таблицу. (Нам известно, что масса всех коробок – 6 кг, количество коробок – 3. Нужно узнать, сколько весит одна коробка печенья..) - И какая краткая запись подойдёт к первой задаче? (К первой задаче подходит таблица 2.) - Давайте устно решим задачу. Вспомним правило: Чтобы найти массу одной коробки, надо массу всех коробок разделить на количество коробок. 6: 3 = 2 (кг.) - масса одной коробки. Ответ: 2 килограмма весит одна коробка печенья. - Рассмотрим вторую задачу. Масса одной коробки печенья 2 кг. Сколько весят 3 таких же коробки печенья? - Устно заполним таблицу. (Нам известно, что масса одной коробки печенья – 2 кг, количество коробок – 3. Нужно узнать, сколько весят все коробки печенья.) - Какая краткая запись подходит ко второй задаче? (Ко второй задаче подходит таблица 3). - Решим устно эту задачу. Вспомним правило: Чтобы найти массу всех коробок, нужно массу одной коробки умножить на количество коробок. 2 × 3 = 6 (кг.) - масса всех коробок с печеньем. Ответ: 6 килограмм весят три коробки с печеньем. - И рассмотрим третью задачу. Масса одной коробки печенья 2 кг. Сколько коробок потребуется, чтобы разложить 6 кг печенья поровну? - Заполним таблицу устно. (Нам известно, что масса одной коробки – 2 кг, масса всех коробок – 6 кг. Нужно узнать количество коробок, чтобы разложить печенье.) - И к третьей задаче подходит... (К третьей задаче подходит таблица 1)
- Решим задачу устно. Вспомним правило: Чтобы найти количество коробок, надо массу всех коробок разделить на массу одной коробки. 6: 2 = 3 (к.) - количество коробок. Ответ: 3 коробки потребуется.
|
Таблица



| |||||||||||||||||
| 2. Осознание постановки задачи. | - Молодцы, теперь открываем учебник на стр. 82 и читаем задачу №4.
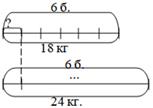
18 кг варенья разложили в 6 банок поровну. Сколько надо таких банок, чтобы разложить 24 кг варенья?
- О чем идёт речь в задаче? (о варенье, что его разложили по банкам)
- Какую тройку величин мы будем использовать? (Масса 1 предмета / Количество предметов / Общая масса)
- Начертите таблицу, мы вместе её заполним.
- Что известно в задаче? (в 6 банках 18 кг варенья) - Записывайте. Что еще известно? (есть 24 кг варенья, которое нужно разложить по банкам. Найти их количество.) - А что вы напишете в первую колонку? Что говорится о массе 1 банки в задаче? (Что варенье разложили по банкам поровну, и нужно найти количество таких же банок. Значит масса 1 банки одинаковая) - Верно.
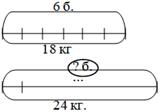
- Перед вами схемы, какая из них подходит к нашей задаче? 1) Ученики говорят, что подходит 2 схема. - Почему не подходят первая и третья схемы? Объясните. (Первая схема не подходит, потому что неправильно поставлены данные. Третья схема не подходит, потому что не хватает данных) - Молодцы. Перечертите схему себе в тетрадь. |  Таблица
Таблица
Схемы
Таблица
Таблица
Схемы
| |||||||||||||||||
| 3. составление плана решения | - Ребята, скажите, можем ли мы сразу ответить на вопрос задачи? (Мы не можем сразу ответить на вопрос задачи)
- Тогда будем рассуждать. Как вы думаете, какой главный вопрос в нашей задаче? (В нашей задаче главный вопрос - Сколько надо банок, чтобы разложить 24кг варенья?)
- Какие две величины нужно знать, чтобы ответить на этот вопрос? (Чтобы ответить на этот вопрос. надо знать общую массу и массу 1 банки)
- Посмотрим по схеме или по таблице, какое из этих двух чисел нам уже известно? (Нам известна общая масса - 24 кг)
- А какое число мы пока не знаем? (Мы не знаем массу 1 банки)
- Значит, чтобы решить задачу надо ответить на этот вопрос. Мы не знаем, массу 1 банки, но что мы можем о ней сказать? (Что она одинаковая в обоих случаях)
- Тогда поднимемся на первую строчку. Какие величины нужно знать, чтобы найти массу 1 банки? (Нужно знать общую массу и количество банок)
- Посмотрим по схеме или по таблице, что нам известно? (Нам известны оба числа, общая масса - 18 кг, количество банок - 6)
По этой беседе одновременно строим «Дерево рассуждений». Начинаем с вопроса.
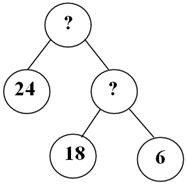 Составляем план решения задачи:
- Зная, что общая масса - 18 кг и количество банок - 6, что мы можем найти? (Мы можем найти массу 1 банки)
- Что для этого надо сделать? (Для этого надо общую массу разделить на количество банок)
- Верно, мы найдем это число, но пока его вычислять не будем.
Составляем план решения задачи:
- Зная, что общая масса - 18 кг и количество банок - 6, что мы можем найти? (Мы можем найти массу 1 банки)
- Что для этого надо сделать? (Для этого надо общую массу разделить на количество банок)
- Верно, мы найдем это число, но пока его вычислять не будем.
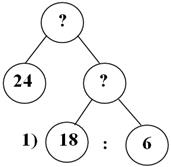 - А теперь зная массу 1 банки и общую массу, что мы можем найти? (Мы можем найти количество банок)
- Что для этого надо сделать? (Для этого надо общую массу разделить на массу 1 банки)
- Всё правильно, но мы пока его тоже не будем вычислять.
- А теперь зная массу 1 банки и общую массу, что мы можем найти? (Мы можем найти количество банок)
- Что для этого надо сделать? (Для этого надо общую массу разделить на массу 1 банки)
- Всё правильно, но мы пока его тоже не будем вычислять.
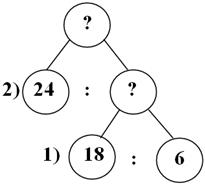
| «Дерево рассуждений» «Дерево рассуждений» «Дерево рассуждений» | |||||||||||||||||
| 4. Запись решения | - Ребята, посмотрите на наше дерево рассуждений и скажите, во сколько действий можно решить задачу? (Задачу можно решить в 2 действия) - Объясните, почему? (Потому что в задаче два неизвестных) - Верно, давайте запишем первое действие. Кто нам его продиктует?(18 разделить на 6 равно 3 килограмма тире масса 1 банки) - Посмотрите на доску, у всех получилась такая же запись? 1) 18: 6 = 3 (кг.) - масса 1 банки. - Теперь запишем второе действие. Кто же нам его продиктует? (24 разделить на 3 равно 8 штук тире количество банок) - Смотрим на доску, у всех так? 2) 24: 3 = 8 (шт.) - количество банок. - Ребята, посмотрите, а это выражение подойдёт к решению нашей задаче? (Да) 24: (18: 6) = 8 (шт.) - количество банок. - Объясните, почему это выражение подходит к решению нашей задачи? (Потому что это одно выражение. Первым действием в скобках мы находим массу одной банки. А вторым действием - деление перед скобками мы находим количество банок, нужное для 24 кг варенья) - Верно. Запишите его себе в тетрадь. | Выражение Выражение Выражение | |||||||||||||||||
| 5. Проверка и исследование полученного решения. | - Ребята, что еще нужно сделать перед тем, как записать ответ? (Нужно сделать проверку решения задачи)
- Правильно. Для этого составим обратную задачу. Как же получить обратную задачу? (Чтобы получить обратную задачу нужно изменить условие и вопрос) - Давайте составим её вместе. 24 кг варенья разложили в... поровну. Сколько килограмм варенья надо наварить, чтобы разложить его в... таких банок? (24 кг варенья разложили в 8 банок поровну. Сколько килограмм варенья надо наварить, чтобы разложить его в 6 таких банок?) - О чем идёт речь в задаче? (о варенье, что его разложили по банкам) - Тройка величин остаётся та же?(да) - Чертим таблицу. - Что известно в задаче? (в 8 банках 24 кг варенья) - Записывайте. Что еще известно? (есть 6 банок, нужно найти массу варенья, которую можно разложить в них поровну.) - А что вы напишете в первую колонку? Что говорится о массе 1 банки в задаче? (Что варенье разложили по банкам поровну. И второй раз раскладывают в такие же банки. Значит масса 1 банки одинаковая) - Верно.
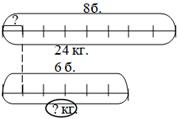
- Рисуем схему. Посмотрите, у всех получилась такая схема?
- Посмотрите на схему и скажите, можем ли мы сразу ответить на вопрос задачи? (Мы не можем сразу ответить на вопрос задачи) - Тогда будем рассуждать. Как вы думаете, какой главный вопрос в нашей задаче? (Главный вопрос - Сколько килограмм варенья надо наварить, чтобы разложить его в 6 таких банок?) - Какие две величины нужно знать, чтобы ответить на этот вопрос? (Чтобы ответить на этот вопрос надо знать массу 1 банки и количество банок) - Посмотрим по схеме или по таблице, какое из этих двух чисел нам уже известно? (Нам известно количество банок их 6.) - А какое число мы пока не знаем? (Мы пока не знаем массу 1 банки) - Значит, чтобы решить задачу надо ответить на этот вопрос. Мы не знаем, массу 1 банки, но что мы можем о ней сказать? (Что она одинаковая в обоих случаях) - Тогда поднимемся на первую строчку. Какие величины нужно знать, чтобы найти массу 1 банки? (Нужно знать общую массу и количество банок) - Посмотрим по схеме или по таблице, что нам известно? (Нам известны оба числа: общая масса - 24 килограмма, количество банок - 8) По этой беседе одновременно строим «Дерево рассуждений». Начинаем с вопроса.
Составляем план решения задачи: - Зная, что общая масса - 24 кг, а количество банок - 8, что мы можем найти? (Мы можем найти массу 1 банки) - Что для этого надо сделать? (Надо общую массу разделить на количество банок) - Верно, мы найдем это число, но пока его вычислять не будем.
- А теперь зная массу 1 банки и количество банок, что мы можем найти? (Мы можем найти общую массу) - Что для этого надо сделать? (Надо количество банок умножить на общую массу)
- Ребята, посмотрите на наше дерево рассуждений и скажите, во сколько действий можно решить задачу? (Задачу можно решить в 2 действия) - Объясните, почему? (Потому что в задаче два неизвестных) - Верно. Запишите решение в тетради. У вас получилась такая же запись? 1) 24: 8 = 3 (кг.) - масса 1 банки. 2) 6 × 3 = 18 (кг.) - общая масса. - А как записать решение одним выражением? Выберите верный. 1) (24: 8) × 3 2) (24: 8) + 3 3) 3 × (24: 8) Учащиеся выбирают и 1, и 3 варианты, так как от перестановки мест произведение не изменяется. - Запишите верный вариант в тетрадь. - Запишем ответ. Кто нам его продиктует? Ответ: 18 килограмм варенья надо наварить. - Всё правильно. А теперь внимательно посмотрите на первую задачу и на обратную ей задачу, что вы видите? (В обратной задаче получили общую массу 18 кг, что соответствует данным исходной задачи) - И что же это значит? (Это значит, что решение и ответ в первой задаче были найдены верно) - Молодцы. Теперь мы уже можем записать ответ к первой (исходной) задаче. Какой будет ответ? Ответ: 8 банок.
| Задача Таблица Схема «Дерево рассуждений» «Дерево рассуждений» «Дерево рассуждений» «Дерево рассуждений» «Дерево рассуждений» Запись Выражения |
Какие зависимости лежат в основе различных способов решения задач на нахождение 4-го пропорционального? Приведите примеры таких задач, которые можно решить разными способами. Покажите, как подвести учащихся к их отысканию, используя необходимые методические приемы.
Задачи на нахождение 4-го пропорционального отражают прямую и обратно пропорциональную зависимость.
1 – 4 вид отражают прямо пропорциональную зависимость. Например, чем больше цена (количество), тем больше стоимость при постоянном количестве (цене). Их вводят в 3 классе.
5 – 6 вид задач на обратно пропорциональную зависимость. Например, чем больше цена, тем меньше количество при постоянной стоимости и наоборот. Их вводят в 4 классе.
Представление об этих зависимостях формируется у детей постепенно в процессе решения таких задач.
Их можно решать двумя способами:
1 способ (основной) – через нахождение постоянной величины.
Например, решим задачу 1го вида из таблицы:
1) 4: 4 = 1 (р.) цена тетради или ручки.
2) 1 ∙ 2 = 2 (р.) стоимость двух ручек.
При решении задачи этим способом полезно опираться на таблицу, т.к. в ней отображена зависимость между тройкой величин.
2 способ – через нахождение коэффициента пропорциональности.
Здесь опираемся на графическую схему
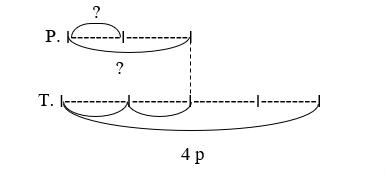
1) 4: 2 = 2 (раза) – во столько раз ручек меньше, чем тетрадей.
Рассуждаем устно: т.к. ручек в 2 раза меньше, чем тетрадей, а цена тетради и ручки одинакова, то и стоимость всех ручек будет в два раза меньше, чем стоимость всех тетрадей
2) 4: 2 = 2 (р.) стоимость ручек.
Этот способ решения возможен, если два данных числа кратны друг другу.
Все задачи на нахождение четвертого пропорционального по программе М.И. Моро вводятся постепенно в 3-4 классах. По мнению авторов, эти задачи нужно вводить друг за другом (с 1 по 6 вид). Работа с каждым видом проводиться в три этапа.
1 этап (1-2- урока) – подготовительная работа – готовим к введению задач этого вида, повторяем зависимости между величинами в тройках и решаем задачи ранее изученных видов.
2 этап (1 урок) – ознакомление с задачами этого вида. Учитель подробно вместе с детьми разбирает, как решают эти задачи. Используя всевозможные виды моделей (реальную, графическую, схематическую и т.д.). В результате дает ученикам образец решения подобных задач. Задачи этого вида могут быть с любой тройкой величин.
3 этап – формирование умения решать задачи данного вида (продолжительный этап). На этом этапе решают множество подобных задач на разных тройках величин, чтобы не сформировать шаблона мышления, рекомендуют включать так же задачи ранее изученных видов.
Примеры таких задач:
1) Паучок за 4 дня сплетает 12 паутинок. Сколько паутинок сплетёт паучок, если будет работать в таком же темпе ещё 9 дней?
2) Из 18 м ткани сшили 6 костюмов для женщин. Сколько таких же костюмов сошьют из 36 м?
3) В зоомагазин привезли желтых и зеленых попугаев. Желтых разместили по 3 попугая в 1 клетке, а зеленых по 9 в клетке. Всего клеток с желтыми попугаями 7. Сколько в зоомагазине клеток с зелёными попугаями, если и желтых и зелёных привезли одинаковое количество?
4) Мама засолила 27 кг белых грибов, по3 кг в каждой банке, и столько же банок опят, по 6 кг в каждой. Сколько килограммов опят засолила мама?
5)18 кг клубничного варенья разложили в банки, по 1,5 кг в каждой. По сколько кг в банке 52 кг малинового варенья, если банок с клубничным и малиновым вареньем получилось одинаковое количество?
6) На 8 костюмов пришивают столько же больших пуговиц, сколько маленьких на 2 таких костюма. Сколько маленьких пуговиц на одном костюме, если больших пуговиц на нём 6?
6. Какую подготовительную работу целесообразно провести перед введением типовых задач на пропорциональное деление и нахождение неизвестного по двум разностям? Приведите примеры подобных упражнений и покажите методику работы с ними. Какие приемы может использовать учитель при ознакомлении учащихся с новыми типами задач? Опишите работу с использованием при этом следующих приемов:
· преобразование задачи известного типа в задачу неизвестного нового типа;
· составление задачи нового типа из нескольких знакомых по типу задач;
· деление задачи «нового» типа на несколько задач известных типов и их последовательное решение;
· предварительное решение задач «нового» типа практическим методом.


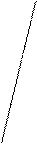



 2)
2)  3)
3) 
 Один ученик у доски, остальные в тетради.
Один ученик у доски, остальные в тетради.