РЕШЕНИЕ ГЕОДЕЗИЧЕСКИХ ЗАДАЧ
НА ТОПОГРАФИЧЕСКИХ ПЛАНАХ И КАРТАХ
Методические указания
Санкт-Петербург
ПГУПС
Приведены основные геодезические задачи, решаемые на топографических картах и планах. Решение типовых задач дано с подробными пояснениями.
Вариантный подбор задач дает возможность проводить проверку знаний студентов. Ответы на большинство задач даны в конце методических указаний.
Предназначены для студентов специальностей СЖД, МТ, ВиВ, ПГС, ПТ и УПП всех форм обучения.
МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
При изображении участков земной поверхности на плане их размеры уменьшают в некоторое число раз. Отношение длины линии на плане к длине горизонтальной проекции соответствующей линии местности называют масштабом плана. Масштаб, выраженный дробью, у которой числитель равен единице, а знаменатель показывает, во сколько раз уменьшены горизонтальные расстояния местности при нанесении их на план, называется численным, например 
, 
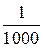и т. п.
Чем больше знаменатель численного масштаба, тем масштаб мельче, чем знаменатель меньше, тем масштаб крупнее.
Масштаб 1: 2 000 показывает, что 1 см на плане соответствует 20 м на местности (так как 2 000 см = 20 м).
С применением масштабов можно решать различные задачи.
Задача № 1. На плане масштаба 1: 500 измерено расстояние а = = 56,5 мм. Определить длину d горизонтального проложения данной линии на местности.
Решение. Вычисление производится по формуле
d = аМ,
где М – знаменатель численного масштаба.
Находим d = 56,5 · 500 = 28 250 мм = 28,25 м.
Задача № 2. Дано горизонтальное проложение линии на местности d = 214 м. Определить длину соответствующего отрезка на плане масштаба 1: 2 000.
|
|
Решение. Используя формулу, приведенную в предыдущей задаче, получим:
а = d / М = 214/2 000 = 0,107 м = 10,7 см.
Задача № 3. Определить масштаб карты в пять раз крупнее масштаба 1: 25 000.
Решение. Зная, что чем меньше знаменатель численного масштаба, тем масштаб крупнее, разделим знаменатель заданного масштаба на 5 и получим масштаб карты 1: 5000.
Следующие задачи предлагается решить самостоятельно (ответы приведены в конце методических указаний).
Задача № 4. На плане масштаба 1: 2 000 измерен отрезок длиной 4,3 см. Определить длину горизонтального проложения данного отрезка на местности.
Задача № 5. Какой отрезок следует отложить на плане масштаба 1: 5 000, если горизонтальное расстояние на местности равно 850 м?
Задача № 6. Определить масштаб карты в два раза мельче масштаба 1: 25 000.
При определении горизонтального проложения между двумя точками вначале необходимо измерить это расстояние на карте, а потом, используя численный масштаб карты, вычислить значение горизонтального проложения на местности. Чтобы не делать вычислений, связанных с использованием численного масштаба, под южной рамкой карты помещен графический (линейный) масштаб. В раствор циркуля берут с карты определяемое расстояние, прикладывают его к линейному масштабу и читают, какому расстоянию на местности оно соответствует. На рис. 1 изображен линейный масштаб для численного 1: 10 000 и показаны расстояния 500 и 540 м.
Рис. 1. Определение расстояния по линейному масштабу
Задача № 7. Определить с помощью линейного масштаба на карте У-34-37-В-в-4 (см. приложение) расстояние между точкой с отметкой 151,8 м (квадрат 65×13) и точкой с отметкой 140,9 м (квадрат 65×13).
|
|
Для более точного измерения и откладывания расстояний на карте используют поперечный масштаб, который обычно выгравирован на металлических линейках, называемых масштабными.
Для построения поперечного масштаба на горизонтальной прямой откладывают несколько раз одинаковый отрезок, называемый основанием масштаба (рис. 2). Левое основание делят на 10 равных частей (малые деления). Из всех полученных точек восставляют перпендикуляры. На перпендикулярах также откладывают по 10 равных частей и через точки отложения проводят линии, параллельные основанию. Затем через деления левого основания проводят наклонные линии, как показано на рис. 2.
Рис. 2. Определение расстояний по поперечному масштабу
Из подобия треугольников BDE и Bde следует Вd / ВD = de / DE, или de = Bd · DE / BD. Но DE =АВ /10, поэтому Bd = ВD / 10. Следовательно, de = АВ / 100, т. е. наименьшее деление поперечного масштаба равно 0,01 основания. Эта величина называется предельной графической точностью поперечного масштаба.
Если основание масштаба равно 2 см, то поперечный масштаб носит название нормального поперечного масштаба.
Для определения расстояния между двумя точками на карте берут это расстояние в раствор циркуля-измерителя и переносят его на нижнюю линию поперечного масштаба. Если между иглами измерителя вмещается целое число оснований и малых делений, то отсчитывают расстояние. Если же левая игла измерителя попадает между двумя наклонными линиями малого деления, то измеритель перемещают вверх, параллельно основанию, пока левая игла не будет точно лежать на наклонной линии. Правая игла при этом должна располагаться на одной из вертикальных линий поперечного масштаба.
|
|
Задача № 8. Определить по схеме нормального поперечного масштаба (рис. 2) длину отрезка 1, измеренного на карте масштаба 1: 10 000.
Решение. По численному масштабу карты определяем, что основанию (AB)поперечного масштаба 2 см соответствует расстояние на местности, равное 200 м. Левое основание разделено на 10 равных делений. Следовательно, малому делению (DE) соответствует расстояние в 20 м. Наименьшее деление поперечного масштаба (de),т. е. предельная графическая точность масштаба, составит 0,1 малого деления и равна 2 м. При определении длины отрезка 1 имеем: 2 · 200м + 6 · 20 м + 3 · 2 м = 526 м.
Задача № 9. Определить по нормальному поперечному масштабу на рис. 2 длину отрезка 2, измеренного на плане масштаба 1: 2 000.
Решение. По численному масштабу плана определяем: основанию 2 см соответствует 40 м; малому делению – 4 м; наименьшему делению – 0,4 м. Искомая длина составит (см. рис. 2): вправо от B одно основание, то есть 40 м; влево от B три малых деления по 4 м, то есть 12 м; вверх по наклонной линии поднялись на 5 наименьших делений по 0,4 м каждое, чему соответствует 2 м. Получаем: 40 + 12 + 2 = 54 м.
Задача № 10. Определить по схеме нормального поперечного масштаба длины отрезков 1 и 3 для карты масштаба 1: 25 000.
Задача № 11. Определить по схеме нормального поперечного масштаба длины отрезков 2 и 4 для плана масштаба 1: 5 000.
Задача № 12. Определить предельную графическую точность следующих поперечных масштабов 1: 500, 1: 2 000, 1: 50 000.
Для измерения расстояния по извилистым дорогам, рекам и другим кривым линиям существуют специальные приборы, которые называют курвиметрами (рис. 3). В основании курвиметр имеет колесико, длина окружности которого известна. Колесиком прибора проводят по измеряемой линии. Вращение колесика передается на стрелку, указывающую на шкале циферблата измеренное расстояние. Для приближенного определения длины кривой линии (при отсутствии курвиметра) можно разбить ее на ряд отрезков, близких к прямым, и измерить ее как сумму прямых отрезков.
Рис. 3. Курвиметр
Задача № 13. Определить криволинейное расстояние по улучшенной грунтовой дороге (карта У-34-37-В-в-4) от населенного пункта Михалино до пересечения ее с шоссе (отметка 144,0 м, квадрат 65×14).