Раздел 5. Основные понятия дискретной математики. Теория вероятности
Тема 5.1. Элементы комбинаторики
План
1. Элементы математической логики.
2. Основные понятия комбинаторики.
3. Задачи для самостоятельного решения.
Элементы математической логики
Математическая логика – это раздел математики, который занимается исследованием высказываний с точки зрения их формального строения.
Опр. Высказывание – это повествовательное предложение, о котором можно однозначно сказать истинно оно или ложно.
Пример 1.1. Высказывания:
1. Москва - столица России. (и)
2. К форменным элементам крови относятся эритроциты, лейкоциты, тромбоциты. (и)
3. Айсберги чаще всего встречаются на экваторе. (л)
4. У здорового человека температура тела 26,6°С. (л)
Опр. Отрицанием высказывания А называется новое высказывание, которое обозначается 
(читается «не А») и истинно, если А ложно, и ложно, если А истинно.
| А |
|
Опр. Дизъюнкцией высказываний А и В называется новое высказывание, которое обозначается 
(читается «А или В») и ложно только в том случае, если ложны оба высказывания, а в остальных случаях истинно.
| А | В | А ∪ В |
Опр. Конъюнкцией высказываний А и В называется новое высказывание, которое обозначается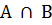 
(читается «А и В») и истинно только в том случае, когда истинны оба высказывания, а в остальных случаях - ложно.
| А | В | А ∩ В |
Каждое составное высказывание можно выразить в виде формулы. Для каждого составного высказывания можно построить таблицу истинности, которая определит его значение для всех возможных исходных значений простых высказываний.
Например, построить таблицу истинности для высказывания: 
| А | В | 
| 
| А ∪ В | 
| 
|
Основные понятия комбинаторики
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и размещения этих элементов в каком-либо порядке.
Опр. Группы составленные из каких – либо элементов называется соединениями.
Опр. Размещением из n-элементов по m в каждом (
) называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения. Количество размещений вычисляется по формуле:
Пример 2.1.
Сколькими способами из 8 кандидатур можно выбрать 5 медсестёр в 5 отделений?
.
Ответ: 6720 размещений.
Опр. Перестановкой из n-элементов называются такие соединения из всех элементов, которые отличаются друг от друга порядком расположения. Количество перестановок вычисляется по формуле:
Пример 2.2.
Найти число вариантов различных списков из 7 пациентов.(Списки считаются разными, если они отличаются порядком расположения элементов.)
= 
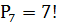Ответ: 5040 списков.
Если возникает необходимость не учитывать порядок следования элементов в размещении, то последовательности называются сочетаниями.
Опр. Сочетанием из n-элементов по m в каждом (
) называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний вычисляется по формуле.
Пример 2.3.
В клетке содержится 10 мышей. Необходимо отобрать 4 мыши для проведения эксперимента. Сколькими способами это можно сделать?
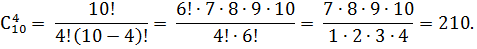
Ответ: 210 способов.
Задачи для самостоятельного решения
1. Построить таблицу истинности для высказывания: 
| А | В |
|
|
| 
| 
|
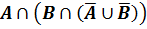
2. Главный врач больницы ежедневно просматривает отчёты о выписке и поступлении больных из 6 отделений. Если порядок просмотра случаен, сколько существует способов их просмотра?
Ответ: 720 способов.
3. Больной принимает четыре лекарства. Последовательность приёма лекарств существенно влияет на результат лечения. Сколько имеется способов приёма этих лекарств?
: 4 способа.
4. В студенческой группе 15 человек. Из них необходимо выбрать старосту группы, профорга и физорга. Сколько возможных вариантов можно составить?
Ответ: 45 различных вариантов.