Основные понятия и теоремы теории вероятностей / Определения вероятностей
Задание № 1
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет нечетное число очков, равна …
Правильное решение:
Для вычисления события 
(на верхней грани выпадет нечетное число очков) воспользуемся формулой 
где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события . В нашем случае возможны 
элементарных исходов испытания (на верхней грани появится одно очко, два очка, …, шесть очков), из которых благоприятствующими являются три исхода (одно очко, три очка и пять очков). Следовательно, 
и 
Основные понятия и теоремы теории вероятностей / Алгебра событий
Задание № 2
Операции сложения и умножения событий не обладают свойством …
Правильное решение:
Операции сложения и умножения событий обладают свойствами:
а) коммутативности сложения 
б) коммутативности умножения 
в) дистрибутивности 
Следовательно, операции сложения и умножения событий не обладают свойством 
Основные понятия и теоремы теории вероятностей / Теоремы сложения и умножения вероятностей
Задание № 3
Устройство состоит из двух элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,85 и 0,75. Тогда вероятность того, что в течение рабочего дня будет работать безотказно только один элемент, равна …
Правильное решение:
Введем обозначения событий: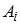 
– в течение рабочего дня безотказно работает 
-ый элемент; A – течение рабочего дня работает безотказно только один элемент. Тогда 
где 
– событие, противоположное событию 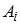, причем 
.
Так как, по условию задачи, события 
и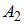 
независимы, то 
|
|
Основные понятия и теоремы теории вероятностей / Полная вероятность и формулы Байеса
Задание № 4
С первого станка на сборку поступает 30%, со второго – 70% всех деталей. Среди деталей первого станка 80% стандартных, второго – 90%. Наудачу взятая деталь оказалась стандартной. Тогда вероятность того, что она поступила на сборку с первого станка, равна …
Правильное решение:
Предварительно вычислим вероятности события (взятая наудачу деталь окажется стандартной) по формуле полной вероятности:
.
Здесь: 
– вероятность того, что деталь поступила с первого станка;
– вероятность того, что деталь поступила со второго станка;
– условная вероятность того, что деталь стандартная, если она изготовлена на первом станке;
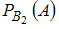– условная вероятность того, что деталь стандартная, если она изготовлена на втором станке.
Тогда 
Теперь вычислим условную вероятность того, что стандартная деталь поступила на сборку с первого станка, по формуле Байеса:
.
Дискретные случайные величины / Законы распределения вероятностей одномерных дискретных случайных вели...
Задание № 5
Дискретная случайная величина 
задана законом распределения вероятностей:
Тогда значение a равно …
Правильное решение:
Так как сумма вероятностей возможных значений равна 1, то 
.
Дискретные случайные величины / Функция распределения вероятностей дискретной случайной величины
Задание № 6
|
|
Дискретная случайная величина задана законом распределения вероятностей:
Тогда ее функция распределения вероятностей имеет вид …
Правильное решение:
По определению 
Тогда
а) при 
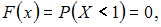
б) при 
в) при 
г) при 
д) при 
Следовательно, 