Задание № 7
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
Правильное решение:
Математическое ожидание дискретной случайной величины вычисляется по формуле: 
. Тогда 
Дискретные случайные величины / Числовые характеристики дискретных случайных величин
Задание № 7
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
Правильное решение:
Математическое ожидание дискретной случайной величины вычисляется по формуле: . Тогда
Дискретные случайные величины / Биномиальный закон распределения вероятностей
Задание № 8
Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,8. Тогда математическое ожидание дискретной случайной величины X – числа появлений события A в 
проведенных испытаниях – равно …
Правильное решение:
Случайная величина X подчиняется биномиальному закону распределения вероятностей.
Поэтому 
Дискретные случайные величины / Простейший поток событий. Распределение Пуассона
Задание № 9
Семена содержат 0,15% сорняков. Тогда вероятность того, что при случайном отборе 2000 сорняков будет обнаружено не более двух семян сорняков, можно определить как …
Правильное решение:
Так как число «испытаний» 
достаточно велико,
а вероятность наступления соответствующего события в одном испытании 
достаточно мала, то воспользуемся формулой Пуассона вида
где 
Тогда
Дискретные случайные величины / Вероятности состояний цепи Маркова
Задание № 10
Матрица вероятностей перехода однородной цепи Маркова имеет вид 
а вектор вероятностей состояний 
цепи Маркова на третьем шаге равен 
Тогда вероятность того, что на втором шаге цепь Маркова находилась в состоянии 
равна …
Правильное решение:
Так как вектор вероятностей 
состояний цепи Маркова на третьем шаге можно вычислить как: 
то 
Вычислим обратную матрицу 
Тогда 
то есть 
Непрерывные случайные величины / Плотность распределения вероятностей непрерывной случайной величины
Задание № 11
Непрерывная случайная величина 
задана плотностью распределения вероятностей:
Тогда вероятность 
равна …
Правильное решение:
Воспользуемся формулой 
Тогда 
Непрерывные случайные величины / Функция распределения вероятностей непрерывной случайной величины
Задание № 12
Непрерывная случайная величина задана функцией распределения вероятностей:
Тогда ее плотность распределения вероятностей имеет вид …
Правильное решение:
Плотность распределения вероятностей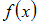 
непрерывной случайной величины находится по формуле: 
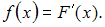Тогда
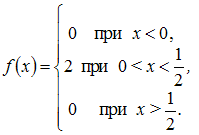
Непрерывные случайные величины / Числовые характеристики непрерывной случайной величины
Задание № 13
Непрерывная случайная величина задана функцией распределения вероятностей:
Тогда ее математическое ожидание равно …
Правильное решение:
Вычислим предварительно плотность распределения вероятностей по формуле: 
Тогда 
и
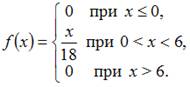Следовательно, 