Определение 2.1 Пусть  и
и  --- конгруэнции на алгебре
--- конгруэнции на алгебре  . Тогда
. Тогда  централизует
централизует  (записывается:
(записывается:  ), если на
), если на  существует такая конгруэнция
существует такая конгруэнция  , что:
, что:
1) из 
всегда следует 
2) для любого элемента 
всегда выполняется 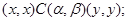
3) если 
то 
Под термином "алгебра" в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие 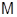 .
.
Следующие свойства централизуемости, полученные Смитом, сформулируем в виде леммы.
Лемма 2.1 Пусть  . Тогда:
. Тогда:
1) существует единственная конгруэнция  , удовлетворяющая определению 2.1;
, удовлетворяющая определению 2.1;
2)  ;
;
3) если 
то 
Из леммы 2.1. и леммы Цорна следует, что для произвольной конгруэнции  на алгебре
на алгебре  всегда существует наибольшая конгруэнция, централизующая
всегда существует наибольшая конгруэнция, централизующая  . Она называется централизатором конгруэнции
. Она называется централизатором конгруэнции  в
в  и обозначается
и обозначается  .
.
В частности, если  , то централизатор
, то централизатор  в
в  будем обозначать
будем обозначать  .
.
Лемма 2.2 Пусть  ,
,  --- конгруэнции на алгебре
--- конгруэнции на алгебре  ,
,  ,
,  ,
,  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1)  ;
;
2)  , где
, где  ;
;
3) если выполняется одно из следующих отношений:
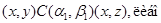


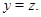
4) из  всегда следует
всегда следует 
Доказательство:
1) Очевидно, что  --- конгруэнция на
--- конгруэнция на  , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и
, удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и  .
.
2)  --- конгруэнция на
--- конгруэнция на  , удовлетворяющая определению
, удовлетворяющая определению
2.1. Значит 
3) Пусть 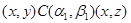 .
.
Тогда 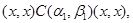

Применим к последним трем соотношениям мальцевский оператор  такой, что
такой, что 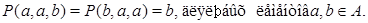
Тогда получим 
т.е. 
Аналогичным образом показываются остальные случаи из пункта 3).
4) Пусть 
Тогда справедливы следующие соотношения:

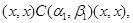
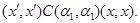
Следовательно, 
где  --- мальцевский оператор.
--- мальцевский оператор.
Тогда 
то есть  .
.
Так как 
то  .
.
Таким образом  . Лемма доказана.
. Лемма доказана.
Следующий результат оказывается полезным при доказательстве последующих результатов.
Лемма. 2.3 Любая подалгебра алгебры  , содержащая диагональ
, содержащая диагональ  , является конгруэнцией на алгебре
, является конгруэнцией на алгебре  .
.
Доказательство:
Пусть 

Тогда из 


следует, что 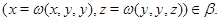
Аналогичным образом из 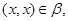


получаем, что 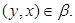
Итак,  симметрично и транзитивно. Лемма доказана.
симметрично и транзитивно. Лемма доказана.
Лемма 2.4 Пусть  . Тогда
. Тогда 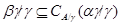 для любой конгруэнции
для любой конгруэнции  на алгебре
на алгебре  .
.
Доказательство:
Обозначим  и определим на алгебре
и определим на алгебре  бинарное отношение
бинарное отношение  следующим образом:
следующим образом: 
тогда и только тогда, когда 
где 

Используя лемму 2.3, нетрудно показать, что  --- конгруэнция на алгебре
--- конгруэнция на алгебре 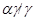 , причем
, причем 
Пусть 
то есть 

Тогда 
и, значит 
Пусть, наконец, имеет место 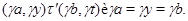
Тогда справедливы следующие соотношения:



применяя мальцевчкий оператор  к этим трем соотношениям, получаем
к этим трем соотношениям, получаем 
Из леммы 2.2 следует, что 
Так как  то
то 
Значит, 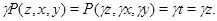
Но  , следовательно,
, следовательно,  .
.
Итак, 
и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5 Пусть 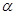 ,
,  --- конгруэнции на алгебре
--- конгруэнции на алгебре  ,
, 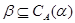 и
и  --- изоморфизм, определенный на
--- изоморфизм, определенный на  .
.
Тогда для любого элемента  отображение
отображение  определяет изоморфизм алгебры
определяет изоморфизм алгебры 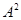 на алгебру
на алгебру  , при котором
, при котором  .
.
В частности,  .
.
Доказательство.
Очевидно, что  --- изоморфизм алгебры
--- изоморфизм алгебры 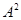 на алгебру
на алгебру 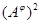 , при котором конгруэнции
, при котором конгруэнции 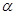 ,
,  изоморфны соответственно конгруэнциям
изоморфны соответственно конгруэнциям 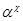 и
и  .
.
Так как 
то определена конгруэнция 
удовлетворяющая определению 2.1.
Изоморфизм  алгебры
алгебры 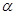 на алгебру
на алгебру  индуцирует в свою очередь изоморфизм
индуцирует в свою очередь изоморфизм  алгебры
алгебры  на алгебру
на алгебру  такой, что
такой, что

для любых элементов  и
и  , принадлежащих
, принадлежащих 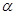 . Но тогда легко проверить, что
. Но тогда легко проверить, что  --- конгруэнция на алгебре
--- конгруэнция на алгебре  , изоморфная конгруэнции
, изоморфная конгруэнции  .
.
Это и означает, что 
Лемма доказана.
Определение 2.2 Если  и
и 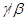 --- факторы на алгебре
--- факторы на алгебре  такие, что
такие, что  то конгруэнцию
то конгруэнцию  обозначим через
обозначим через  и назовем централизатором фактора
и назовем централизатором фактора  в
в  .
.
Определение 2.3 Факторы  и
и 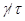 назыавются перспективными, если либо
назыавются перспективными, если либо 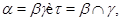 либо
либо 
Теорема Пусть 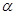 ,
,  ,
,  ,
,  --- конгруэнции на алгебре
--- конгруэнции на алгебре  . Тогда:
. Тогда:
1) если  , то
, то 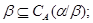
2) если 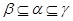 , то
, то 

3) если  ,
,  и факторы
и факторы  ,
, 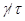 перспективны, то
перспективны, то 
4) если  - конгруэнции на
- конгруэнции на  и
и  , то
, то 
где  ,
, 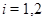 .
.
Доказательство.
1) Так как конгруэнция  централизует любую конгруэнцию и
централизует любую конгруэнцию и 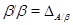 , то
, то 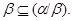
2) Из первого пункта лемы 2.2 следует, что 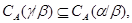
а в силу леммы 2.4 получаем, что 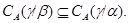
Пусть  - изоморфизм
- изоморфизм 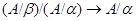 . Обозначим
. Обозначим

По лемме 2.5  , а по определению
, а по определению 
Следовательно, 
3) Очевидно, достаточно показать, что для любых двух конгруэнции  и
и  на алгебре
на алгебре  имеет место равенство
имеет место равенство 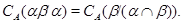
Покажем вналале, что 
Обозначим  . Тогда, согласно определению 2.1. на алгебре
. Тогда, согласно определению 2.1. на алгебре  существует такая конгруэнция
существует такая конгруэнция  , что выполняются следующие свойства:
, что выполняются следующие свойства:
а) если  , то
, то 
б) для любого элемента  ,
, 
в) если 

то 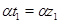
Построим бинарное отношение  на алгебре
на алгебре 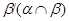 следующим образом:
следующим образом: 
тогда и только тогда, когда 
и 
Покажем, что  --- конгруэнция на
--- конгруэнция на 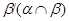 .
.
Пусть 
для  . Тогда
. Тогда 
и 
Так как 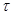 --- конгруэнция, то для любой
--- конгруэнция, то для любой  -арной операции
-арной операции 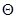 имеем
имеем

Очевидно, что 
и 
Следовательно, 
Очевидно, что для любой пары 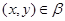

Значит, 
Итак, по лемме 2.3,  - конгруэнция на
- конгруэнция на 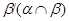 . Покажем теперь, что
. Покажем теперь, что  удовлетворяет определению 2.1, то есть
удовлетворяет определению 2.1, то есть  централизует
централизует  . Пусть
. Пусть 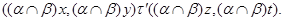
Тогда 
Так как 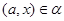 ,
,  и
и  , то
, то  . Следовательно,
. Следовательно,  удовлетворяет определению 2.1.
удовлетворяет определению 2.1.
Если  , то
, то 
значит, 
Пусть, наконец, имеет место (1) и 
Тогда 
Так как  и
и  , то
, то  , следовательно,
, следовательно,  . Из (2) следует, что
. Из (2) следует, что  , а по условию
, а по условию  . Значит,
. Значит,  и поэтому
и поэтому

Тем самым показано, что конгруэнция  удовлетворяет определению 2.1, то есть
удовлетворяет определению 2.1, то есть  централизует
централизует  .
.
Докажем обратное включение.
Пусть 
Тогда на алгебре  определена конгруэнция
определена конгруэнция  удовлетворяющая определению 2.1. Построим бинарное отношение
удовлетворяющая определению 2.1. Построим бинарное отношение  на алгебре
на алгебре 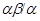 следующим образом:
следующим образом:

тогда и только тогда, когда
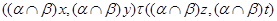
и  ,
,  .
.
Аналогично, как и выше, нетрудно показать, что  --- конгруэнция на алгебре
--- конгруэнция на алгебре 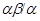 . Заметим, что из доказанного включения в одну сторону следует, что
. Заметим, что из доказанного включения в одну сторону следует, что  . Покажем поэтому, что
. Покажем поэтому, что  централизует
централизует 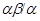 .
.
Так как 
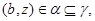
 то
то 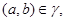
то есть  удовлетворяет условию 1) определения 2.1.
удовлетворяет условию 1) определения 2.1.
Если  , то
, то 
следовательно, 
Пусть имеет место (3) и  .
.
Так как 
то 
Из (4) следует, что  , следовательно,
, следовательно, 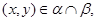
то есть 
На основании леммы 2.2 заключаем, что 
Следовательно,  .
.
А так как  , то
, то  , то есть
, то есть 
4) Обозначим  . Пусть
. Пусть 
и удовлоетворяет определению 2.1.
Определим бинарное отношение  на
на  следующим образом
следующим образом
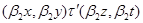
тогда и только тогда, когда

Аналогично, как и выше, нетрудно показать, что  --- конгруэнция, удовлетворяющая определению 2.1.
--- конгруэнция, удовлетворяющая определению 2.1.
Это и означает, что 
Теорема доказана.
Как следствия, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.