Основные понятия и определения
Пусть задана бесконечная числовая последовательность 
:
, … (1.1)
В прошлом году мы определяли числовую последовательность как функцию натурального аргумента. Это означает, что каждый член последовательности является функцией своего номера п: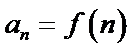 
. В дальнейшем иногда будем рассматривать и п, равное нулю, поэтому числовую последовательность будем определять как функцию целочисленного аргумента (от слов «целое число»).
Определение 1. Выражение
(1.2)
называется бесконечным числовым рядом, или, короче, рядом. Члены последовательности 
,… называются членами ряда; выражение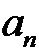 
с индексом п - общим членом ряда.
Отличить последовательность от ряда просто: члены последовательности пишутся через запятую, члены ряда соединены знаками плюс.
Таким образом, понятие ряда является обобщением суммирования на случай бесконечного числа слагаемых.
Ряд считается заданным, если известна (задана) формула его общего члена. Общий член ряда (1.2) совпадает с общим членом последовательности (1.1) и также является функцией целочисленного аргумента n, т.е. 
. Например, если задан общий член в виде
, (1.3)
то, полагая в этой формуле n = 1, 2, 3,..., можно найти любой член ряда, а тем самым и весь ряд:
- члены последовательности или члены ряда,
(1.4)
-числовой ряд.
Определение. Сумма n первых членов ряда называется n- ой частичной суммой ряда и обозначается символом 
:
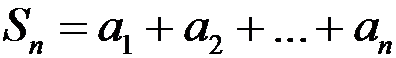. (1.5)
Можно записать так: 
.
В частности,
,
. (1.6)
Составим из всех частичных сумм ряда (1.2) числовую последовательность 
:
(1.7)
Она называется последовательностью частичных сумм. Как всякая числовая последовательность, она может иметь предел, т.е. сходиться, или не иметь предела, т.е. расходиться. Предел последовательности частичных сумм, если он существует, будем обозначать буквой S.
|
|
Определение. Ряд называется сходящимся (ряд сходится), если сходится последовательность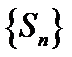 
частичных сумм этого ряда. При этом предел S последовательности частичных сумм 
называется суммой данного ряда, т.е.
. (1.8)
Для сходящегося ряда, имеющего сумму S, можно формально записать равенство:
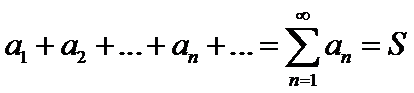. (1.9)
Ряд, не имеющий суммы (1.8), называют расходящимся. В частности, если 
, то говорят, что ряд расходится к 
, и в этом случае используют символическое равенство
.
Замечание. Из равенства (1.6) следует, что любой член ряда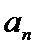 
можно представить как разность частичных сумм и 
:
. (1.10)
Изобразим геометрически последовательность частичных сумм. На рис.1.1,а и б ряд сходится, на рис.1.1,в - расходится.
|
|
в)
|
Рис.1.1
Замечание 3. Иногда номер члена ряда начинается с нуля: 
.
Примеры числовых рядов. Вычисление суммы ряда
Пример 1 º.
1 + 1 + 1 +... + 1 +...
Здесь 
, 
.
Данный ряд расходится Þ 1 + 1 + 1 +... + 1 +...=+¥.
Пример 2 º.
Как обычно, чередование знаков + и - задается с помощью степени (-1). Здесь последовательность частичных сумм 
имеет вид:
т.е. значение частичной суммы зависит от чётности номера п:
Таким образом, чётные и нечётные частичные суммы стремятся к двум различным пределам:
чётные к нулю, нечётные - к единице:
|
Рис.1.2
Следовательно, последовательность 
не имеет предела, и данный ряд расходится.
Пример 3 º.
1 + 2 + 3 +... + n +...
Это арифметическая прогрессия с разностью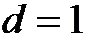 
. Напомним, что название «арифметическая» происходит оттого, что каждый член этой прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:
|
|
.
В данной прогрессии 
, а последовательность частичных сумм имеет вид:
Найдем предел 
.
Следовательно, данный ряд расходится Þ 1 + 2 + 3 +... + n +...=+¥.
Пример 4 º.
Здесь общий член ряда можно преобразовать, разложив на простейшие дроби:
.
Тогда ряд примет вид:
Вычислим частичную сумму, раскрыв скобки:
Предел последовательности частичных сумм
Þ сумма ряда конечна, т. е. ряд сходится Þ
=1.
Пример 5º.
.
Вывод будет дан ниже. Этот ряд называется рядом Лейбница.
Пример 6º.
.
Вывод будет дан ниже. Здесь в знаменателе только нечётные числа.
Пример 7º.
. Вывод будет дан ниже.
Пример 8º.
Вывод будет дан ниже. Сумма ряда равна числу е - основанию натурального логарифма.
Сумму ряда вычислить не всегда легко и даже не всегда возможно. Поэтому в теории рядов чаще решается более простая задача - выяснение, сходится ряд или расходится. Это называется исследованием сходимости ряда.