Цель работы
Изучение конструкций и характеристик коаксиальных кабелей связи, ознакомление с образцами кабельной продукции различных типов, получение навыков по расчету первичных и вторичных параметров.
Расчет первичных и вторичных параметров кабеля
Таблица 1 – Исходные данные коаксиального кабеля
| № варианта | Тип кабеля, мм | Материал проводников | Тип изоляции | Частота, МГц |
| 2,6/9,5 | Медь-медь | Полиэтиленовая спираль |
Коаксиальные кабели обычно используются в диапазоне частот свыше 60 кГц, при этом расчет первичных параметров на этих частотах можно производить по упрощенным формулам.
1 Активное сопротивление коаксиальной пары состоит из сопротивления внутреннего проводника 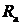 и внешнего (полого) проводника
и внешнего (полого) проводника  и рассчитывается из выражения
и рассчитывается из выражения

где f ‒ частота, при которой производится расчет, Гц;
 мм – радиус внутреннего проводника;
мм – радиус внутреннего проводника;
 мм – радиус внешнего проводника.
мм – радиус внешнего проводника.
Таблица 2 – Зависимость сопротивления коаксиальной пары от частоты
| f, МГц | ||||
| R, Ом/км | 40,95384615 | 91,575584 | 129,50743 | 317,22713 |

Рисунок 1 ‒ Зависимость сопротивления коаксиальной пары от частоты
2 Индуктивность цепи L состоит из наружной межпроводниковой индуктивности и внутренней индуктивности внутреннего и внешнего проводника и определяется на частотах > 60 кГц по формуле:
 .
.
Таблица 3 – Зависимость индуктивности коаксиальной пары от частоты
| f, МГц | ||||
| L, Гн/км | 0,00026568 | 0,0002621 | 0,0002612 | 0,00026 |

Рисунок 2 ‒ Зависимость индуктивности коаксиальной пары от частоты
3 Емкость коаксиальной пары аналогична емкости цилиндрического конденсатора. Его электрическое поле создается между двумя цилиндрическими поверхностями с общей осью. Емкость определяется по формуле:

где  ‒ эквивалентная относительная диэлектрическая проницаемость изоляции.
‒ эквивалентная относительная диэлектрическая проницаемость изоляции.
Тогда 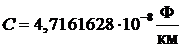 при любых частотах.
при любых частотах.

Рисунок 3 ‒ Зависимость емкости коаксиальной пары от частоты
4 Проводимость изоляции характеризует потери энергии в изоляции проводников коаксиальной пары. Проводимость изоляции обусловлена сопротивлением изоляции изолирующего материала и диэлектрическими потерями. В используемом диапазоне частот (>60 кГц) первой составляющей можно пренебречь. Тогда проводимость изоляции определяется из выражения:
 ,
,
где 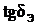 ‒ эквивалентная величина тангенса угла диэлектрических потерь, определяется из таблицы 4.
‒ эквивалентная величина тангенса угла диэлектрических потерь, определяется из таблицы 4.
Таблица 4 – Зависимость tgδэ от типа кабеля и частоты
| Тип кабеля | Тип изоляции | tgδэ.10-4 при частоте, МГц | |||
| 2,6/9,5 | Полиэтиленовая спираль | 0,4 | 0,4 | 0,5 | 0,6 |
Таблица 5 – Зависимость проводимости изоляции от частоты
| f, МГц | ||||
| G, См/км | 
| 
| 
| 
|

Рисунок 4 – Зависимость проводимости изоляции от частоты
5 Волновое сопротивление в общем случае определяется выражением
 .
.
В области высоких частот (при f >40 кГц) волновое сопротивление можно определить по формуле:
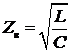 .
.
Таблица 6 – Зависимость модуля волнового сопротивления от частоты
| f, МГц | ||||
 , Ом/км , Ом/км
| 75,05593454 | 74,54853547 | 74,42043287 | 74,24928562 |

Рисунок 5 – Зависимость модуля волнового сопротивления от частоты
6 В области высоких частот (при f >40 кГц) коэффициент затухания определяется по формуле:

Таблица 7 – Зависимость коэффициента затухания от частоты
| f, МГц | ||||
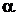 , дБ/км , дБ/км
| 2,373596107 | 5,354140207 | 7,596046672 | 18,78463224 |

Рисунок 6 – Зависимость коэффициента затухания от частоты
7 Коэффициент фазы определяет угол сдвига между током (или напряжением) на протяжении одного километра. Для определения коэффициента фазы в областях высоких частот (при f >40 кГц) можно пользоваться выражением
 .
.
Таблица 8 – Зависимость коэффициента фазы от частоты
| f, МГц | ||||
 , дБ/км , дБ/км
| 22,240968 | 110,45307 | 220,52653 | 1320,1163 |

Рисунок 7 – Зависимость коэффициента фазы от частоты
8 Модуль коэффициента распространения определяется из формулы:
 .
.
Таблица 9 – Зависимость коэффициента распространения от частоты
| f, МГц | ||||
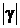 , 1/км , 1/км
| 2,288838663 | 3,360771279 | 3,973070768 | 6,148495276 |

Рисунок 8 – Зависимость модуля коэффициента распространения от частоты
9 Скорость распространения электромагнитной энергии  является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:
является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:
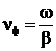 .
.
Таблица 10 – Зависимость коэффициента фазы от частоты
| f, МГц | ||||
 , км/с , км/с
| 282505,03 | 284427,83 | 284917,43 | 285574,17 |

Рисунок 9 – Зависимость скорости распространения энергии от частоты
Вывод
В ходе данной лабораторной работы были рассчитаны первичные и вторичные параметры заданного коаксиального кабеля.
Внутренний проводник данного кабеля – медная проволока диаметром 2,6 мм, на который накладывают спираль из полиэтиленового материала с различным шагом – в зависимости от требований к гибкости кабеля. Диаметр корделя применяют таким, чтобы обеспечить получение заданных электрических характеристик кабеля.
Внешний проводник кабеля изготавливается из медной проволоки диаметром 9,5 мм.
Такой кабель применяется для многоканальной связи и телевидения, с рабочим диапазоном частот до 60 МГц.