Задачи №1-10.
1. В ящике 7 белых и 9 черных шаров. Наугад вынимают 2 шара. Найти вероятность того, что будут вынуты шары разного цвета.
2. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.
3. На складе имеется 15 холодильников, причем 10 из них изготовлены на Минском заводе. Найти вероятность того, что среди взятых наудачу 5 холодильников окажутся 3 холодильника Минского завода.
4. В лотерее участвуют 10 билетов, 4 из которых выигрывают. У одного из участников на руках 3 билета. Найти вероятность того, что 2 из них выиграют.
5. В партии из 12 деталей имеется 7 стандартных. Наудачу отобраны 5 деталей. Найти вероятность того, что среди отобранных деталей будет ровно 3 стандартных.
6. В группе, состоящей из 4 женщин и 3 мужчин, разыгрываются 4 билета в театр. Найти вероятность того, что среди обладателей билетов женщин и мужчин будет поровну.
7. В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных изделий будет ровно одно окрашенное.
8. В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 путевок. Найти вероятность того, что среди обладателей путевок окажутся две девушки.
9. Из партии, в которой 10 деталей без дефекта и 5 с дефектом, берут наудачу 3 детали. Найти вероятность того, что среди них будет ровно одна деталь с дефектом.
10. В офисе работают 6 мужчин и 4 женщины. Компьютер случайным образом отобрал 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.
Задачи №11-20.
1. В группе 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,90, для велосипедиста – 0,80, для бегуна – 0,75. Найти вероятность того, что наудачу вызванный спортсмен выполнит квалификационную норму.
2. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,1 % брака, второй – 0,2 %, третий – 0,3 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго – 2000, а с третьего – 3000 деталей.
3. В трех киосках продаются 1000 лотерейных билетов, из них 400 в первом киоске, 300 – во втором. Среди билетов первого киоска 20 выигрышных, второго – 12, третьего – 18 выигрышных билета. Найти вероятность выигрыша на билет, купленный в наудачу выбранном киоске.
4. На фабрике изготовляющей болты, первая машина производит 30 %, вторая – 25 %, третья – 45 % всех изделий. Брак в их работе составляет соответственно 2 %, 1 %, 3 %. Найти вероятность того, что наугад выбранный болт дефектный.
5. В цехе три модели станков производят одинаковые детали, которые отправляются на общий склад. Станков модели «А» в цехе 5 штук, модели «Б» – 3 штуки и модели «В» – 2 штуки. Станки модели «А» производят 0,94 деталей отличного качества, модели «Б» – 0,9 и модели «В» – 0,85. Найти вероятность того, что взятая наугад со склада деталь окажется отличного качества.
6. Партия лампочек на 20 % изготовлена первым заводом, на 30 % – вторым, на 50 % – третьим. Вероятности выпуска бракованных лампочек соответственно равны: q1 = 0,01, q2 = 0,005, q3 =0,006. Найти вероятность того, что наудачу взятая лампочка будет годной.
7. На базе находятся костюмы, изготовленные на трех фабриках. Из них 30 % изготовлено на первой, 50 % на второй и 20 % на третьей фабрике. Из каждых 100 костюмов, изготовленных на первой фабрике, 60 не имеют никаких дефектов, а на второй и третьей фабрике соответственно, 70 и 80 костюмов без дефектов. Найти вероятность того, что взятый наудачу с базы костюм будет иметь дефект.
8. На трех станках обрабатываются однотипные детали, которые складываются в один ящик. Вероятность брака для первого станка равна 0,02, для второго - 0,03, для третьего – 0,04. Производительность первого станка в 3 раза больше, чем второго, а третьего – в 2 раза меньше, чем второго. Найти вероятность того, что взятая наудачу из ящика деталь будет бракованной.
9. В группе из 30 человек 5 отличников, 10 хорошистов, остальные студенты имеют удовлетворительную успеваемость. Вероятность правильного ответа на экзаменационный вопрос для отличников составляет 0,95, для хорошистов – 0,8 и для троечников – 0,7. К преподавателю наудачу подходит студент из группы. Найти вероятность того, что он правильно ответит на заданный вопрос.
10. Магазин получает часы одной марки от трех разных производителей. Первый завод производит 20 % всей продукции, второй – 30 %, остальные часы производит третий завод. В продукции первого завода спешат 5 % всех часов, второго – 3 %, третьего – 2 %. Найти вероятность того, что купленные в магазине часы спешат.
Задачи №21-30.
1. Посажено 5 семян, всхожесть которых составляет 80 %. Найти вероятность того, что весной будет 2 всхода.
2. Вероятность попадания в цель 0,6. Произведено 4 выстрела. Найти вероятность того, что из них выстрелов будет 2 попадания.
3. В сентябре в среднем 12 дождливых дней. Найти вероятность того, что за неделю будет 3 дождливых дня.
4. Какова вероятность того, что в семье из 5 детей будет точно 3 мальчика? Считать, что вероятность появления мальчика или девочки одинакова.
5. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет 4 раза.
6. Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.
7. Вероятность взрыва при химической реакции равна 0,1. Найти вероятность того, что в серии из 8 синтезов взрыв произойдет 3 раза.
8. В цехе работают 4 станка. Вероятность остановки каждого из них в течение смены равна 0,8. Найти вероятность того, что в течение часа остановится 3 станка.
9. Вероятность того, что покупателю потребуется обувь 43-го размера, равна 0,2. Найти вероятность того, что из первых 5 покупателей обувь этого размера потребуется двоим.
10. В мастерской работают 6 моторов. Для каждого из них вероятность перегрева к обеденному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву перегреются 4 мотора.
Задачи № 31-40.
Случайная величина Х распределена по нормальному закону. Известно её математическое ожидание а и среднее квадратическое отклонение s. 1)Найти вероятность того, что Х примет значение, принадлежащее интервалу (a, b). 2) Найти вероятность того, что абсолютная величина отклонения Х - а окажется меньше d. Конкретные значения параметров заданы в таблице.
| Номер задачи | а | s | a | b | d |
Задачи №41-50.
Закон распределения дискретной случайной величины Х задан в таблице. Найти: 1)математическое ожидание, дисперсию и среднее квадратическое отклонение; 2) вычислить математическое ожидание и дисперсию случайной величины 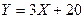 , пользуясь свойствами математического ожидания и дисперсии.
, пользуясь свойствами математического ожидания и дисперсии.
| Номер задачи | Условие задачи | |||||
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 |
Задачи №51-60.
Дана интегральная функция F(x) распределения непрерывной случайной величины. Требуется: 1) убедиться, что заданная функция F(x) является функцией распределения, проверив свойства функции; 2) найти плотность данного распределения f(x); 3) построить графики интегральной и дифференциальной функций распределения.
51) 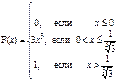 ; 52)
; 52) 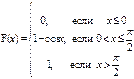 ; 53)
; 53) 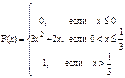 ; 54)
; 54) 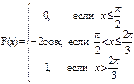 ;
;
55) 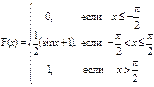 ; 56)
; 56) 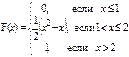 ; 57)
; 57) 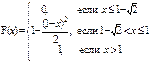 ; 58)
; 58)
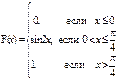 ; 59)
; 59) 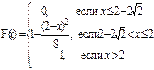 ; 60)
; 60) 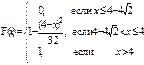 .
.
Задачи №61-70.
Рассчитать и построить гистограмму относительных частот по сгруппированным данным случайной величины Х, где mi – частота попадания вариант в промежуток (хi, хi+1).
| Номер задачи | Условие задачи | Номер задачи | Условие задачи | ||||
| i | xi<X  xi+1 xi+1
| mi | i | xi<X  xi+1 xi+1
| mi | ||
| 2 - 4 | 3 – 7 | ||||||
| 4 - 6 | 7 – 11 | ||||||
| 6 - 8 | 11 – 15 | ||||||
| 8 - 10 | 15 – 19 | ||||||
| 10 - 12 | 19 - 23 | ||||||
| i | xi<X  xi+1 xi+1
| mi | i | xi<X  xi+1 xi+1
| mi | ||
| (-6)– (-2) | 4 – 8 | ||||||
| (-2)– 2 | 8 – 12 | ||||||
| 2 – 6 | 12 – 16 | ||||||
| 6 – 10 | 16 – 20 | ||||||
| 10 - 14 | 20 - 24 | ||||||
| i | xi<X  xi+1 xi+1
| mi | i | xi<X  xi+1 xi+1
| mi | ||
| 7 – 9 | 5 – 8 | ||||||
| 9 – 11 | 8 – 11 | ||||||
| 11 – 13 | 11 – 14 | ||||||
| 13 – 15 | 14 – 17 | ||||||
| 15 - 17 | 17 - 20 | ||||||
| i | xi<X  xi+1 xi+1
| mi | i | xi<X  xi+1 xi+1
| mi | ||
| 4 – 6 | 1 – 5 | ||||||
| 6 – 8 | 5 – 9 | ||||||
| 8 – 10 | 9 – 13 | ||||||
| 10 – 12 | 13 – 17 | ||||||
| 12 - 14 | 17 - 21 | ||||||
| 10 – 14 | 20 – 22 | ||||||
| 14 – 18 | 22 – 24 | ||||||
| 18 – 22 | 24 – 26 | ||||||
| 22 – 26 | 26 – 28 | ||||||
| 26 - 30 | 28 - 30 |
Задачи №71-80.
На основании данного распределения выборки найти выборочное среднее, смещённую и несмещенную выборочные дисперсии. Построить полигон частот.
| Номер задачи | Условие задачи | |||||
| xi | -6 | -2 | ||||
| ni | ||||||
| xi | -10 | -5 | -1 | |||
| ni | ||||||
| xi | ||||||
| ni | ||||||
| xi | ||||||
| ni | ||||||
| xi | 0,01 | 0,04 | 0,08 | 0,14 | 0,16 | |
| ni | ||||||
| xi | ||||||
| ni | ||||||
| xi | ||||||
| ni | ||||||
| xi | ||||||
| ni | ||||||
| xi | 0,2 | 0,3 | 0,5 | 0,6 | 0,9 | |
| ni | ||||||
| xi | ||||||
| ni |