Пример выполнения задания.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Тульский государственный университет»

 

 

КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫСТУДЕНТОВ

ПО КУРСУ «МАТЕМАТИКА» (ПЕРВЫЙ СЕМЕСТР)

Тула 2012

 

Рассмотрено и утверждено на заседании кафедры математического моделирования механико-математического факультета,

протокол № 11 от "21" июня 2011 г.

 

Данные методические указания написаны в помощь студентам экономических специальностей для самостоятельной работы в первом семестре. Рассмотрены решения типовых задач по аналитической геометрии и линейной алгебре, введению в математический анализ, а также даны необходимые теоретические сведения и ссылки на литературу.

 

ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ

 

Задача 1.

Теоретические сведения.

В прямоугольной декартовой системе координат Oxyz положение любой точки задается тремя числами – координатами: 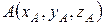(рисунок 1).

 

 

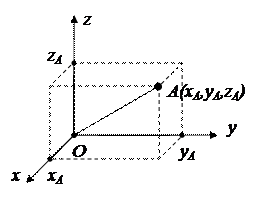
Рисунок 1.

 

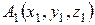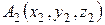Расстояние между двумя точками и определяется по формуле

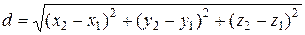. (1)

При решении задач аналитической геометрии на плоскости необходимы следующие сведения о прямой линии:

1) если точка М(x; y) делит отрезок М₁М₂ (М₁(х₁; у₁) и М₂(х₂; у₂)) в отношении λ, то координаты этой точки выражаются формулами

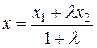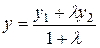, , (2)

если же точка М(x; y) - середина отрезка М₁М₂, то

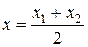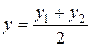, ; (3)

2) уравнение прямой, проходящей через точку М₁(x₁; y₁) и имеющей данный угловой коэффициент k, записывается в виде

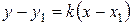; (4)

3) уравнение прямой, проходящей через две данные точки М₁(x₁; y₁) и М₂(x₂; y₂), имеет вид

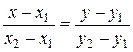, при этом 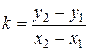; (5)

4) острый угол между двумя прямыми с угловыми коэффициентами k₁ и k₂ определяется по формуле

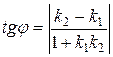, (6)

при этом условие параллельности прямых имеет вид k₁=k₂, а условие перпендикулярности 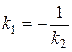; (7)

5) если прямая на плоскости задана общим уравнением Ах+Ву+С=0, то 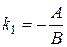- ее угловой коэффициент;

6) если в общем уравнении прямой поделить все члены на , получим уравнение прямой в отрезках:

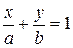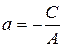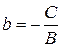, где , ; (8)

7) точка пересечения двух прямых А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0 определяется из решения системы уравнений

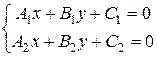. (9)

Уравнение окружности с центром в точке 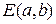и радиусом R имеет вид
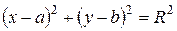. (10)

Пример выполнения задания.

Даны вершины треугольника АВС: А (– 4;8), В (5; – 4), С (10;6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС в общем виде и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD в общем виде и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр.

 

Решение:

1) Расстояние d между двумя точками на плоскости определяется по формуле (1), в которую подставлены значения координат точек А и В (положим 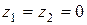), тогда

.

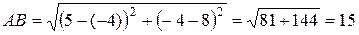2) Уравнение прямой, проходящей через две заданные точки имеет вид (5):

Подставив в (5) координаты точек А и В, получим уравнение прямой АВ:

, , ,

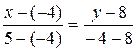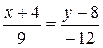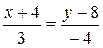, или (АВ).

Для нахождения углового коэффициента k_AB прямой АВ разрешим полученное уравнение относительно y: . Отсюда . Подставив в формулу (5) координаты точек А и С, найдем уравнение прямой АС: , , ,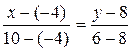

 

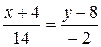или x + 7y – 52 = 0 (AC).

 

Отсюда .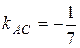

3) Угол между двумя прямыми, угловые коэффициенты которых равны k₁ и k₂, определяется по формуле (6). Угол А, образованный прямыми АВ и АС, найдем по формуле (6), подставив в нее , .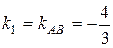

,

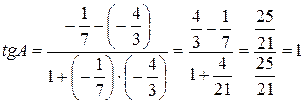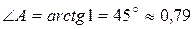рад.

4) Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых связаны соотношением (7), поэтому

.

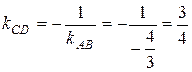Уравнение прямой, проходящей через заданную точку в заданном угловым коэффициентом k направлении, имеет вид (4). Подставив в (4) координаты точки С и 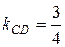, получим уравнение высоты СD:

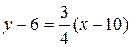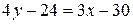, , (CD).

Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (СD):

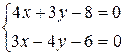, откуда х = 2, y = 0, то есть D (2;0).

Подставив в формулу (1) координаты точек С и D, находим:

.

 

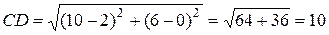5) Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулой (3) деления отрезка пополам, получим:

, .

Следовательно, Е (6; 3) и 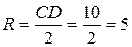. Используя формулу (10), получаем уравнение искомой окружности: (х – 6)²+(y – 3)² = 25.

Задача 2.

Теоретические сведения.

Если известны начало вектора 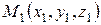и конец 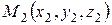, то координаты вектора 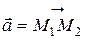находятся по формулам

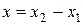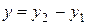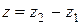, , , (11)

а его длина определяется выражением

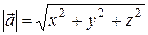. (12)

Вектор 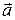с координатами 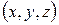может быть представлен разложением по ортам в виде

. (13)

Если α, β, γ – углы, которые вектор 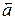образует с положительными направлениями осей координат, то cosα, cosβ, cosγ называются направляющими косинусами вектора 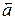(рисунок 2). Тогда имеют место соотношения

, , , .

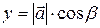Для векторов 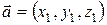и 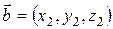вводятся операции с ложения и умножения на число такие, что
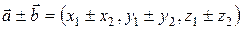и ,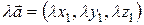

где 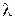− любое число.

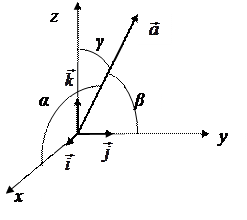
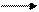Рисунок 2.

Скалярным произведением двух векторов 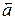и 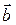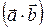называется число, равное произведению длин этих векторов на косинус угла 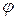между ними, 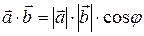или, если векторы заданы своими координатами, то

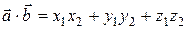. (14)

Векторы, лежащие на одной или параллельных прямых, называют коллинеарными. Признак коллинеарности векторов 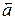и 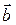является пропорциональность их координат:

. (15)

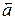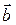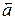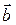Если векторы и взаимно перпендикулярны, то . Угол между векторами и определяется соотношением:

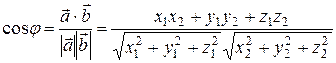. (16)

Уравнение плоскости, проходящей через точку перпендикулярно вектору 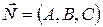, имеет вид

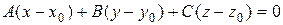. (17)